
- •Власов м. П.
- •1.Постановка задачи
- •2. Задача максимизации выпуска в заданном ассортименте
- •3. Задача загрузки оборудования
- •4. Модели распределения транспортных потоков
- •5. Простейшая задача размещения на сети
- •6. Математические модели спроса и потребления
- •7. Модели равновесия при неравновесных ценах
- •8. Модели рационируемого равновесия
- •9. Особенности метода решения распределительной задачи
- •10. Задачи с разрывной целевой функцией
- •Литература
5. Простейшая задача размещения на сети
Простейшая задача
размещения на сети
– это математическая формализация,
используемая в процессе принятия решения
по выбору пунктов размещения предприятий,
производящих однородную продукцию для
удовлетворения заданного спроса. Пусть
имеется
![]() возможных пунктов размещения предприятий
и
возможных пунктов размещения предприятий
и![]() пунктов потребления (точек спроса),
пунктов потребления (точек спроса),![]() ,
расположенных в узлах сети
,
расположенных в узлах сети![]() ,
где
,
где![]() - множество вершин,
- множество вершин,![]() - множество ребер сети. Заданы величины
- множество ребер сети. Заданы величины![]() ,
,![]() ;
;![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
где
,
где
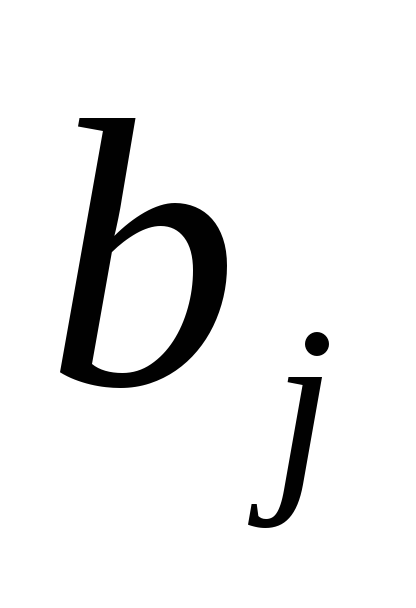 = спрос в пункте
потребления
= спрос в пункте
потребления
 ;
;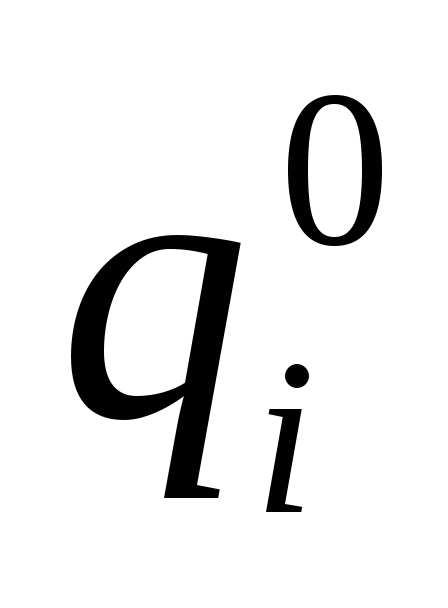 - затраты на ввод
в действия предприятия
- затраты на ввод
в действия предприятия
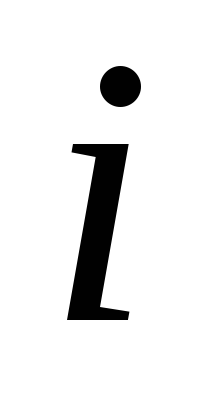 ;
;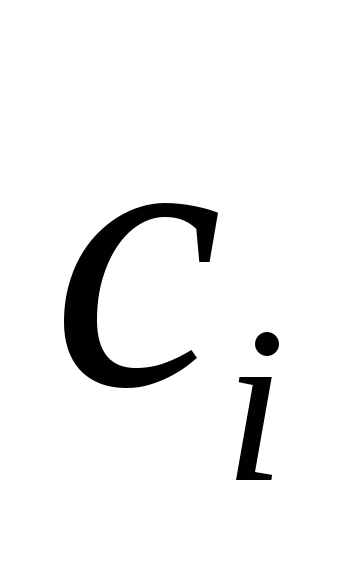 - стоимость
производства единицы продукции в пункте
размещения
- стоимость
производства единицы продукции в пункте
размещения
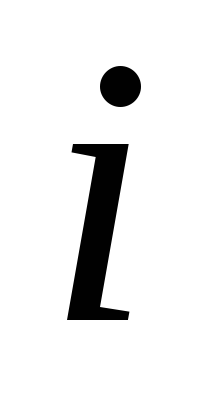 ;
;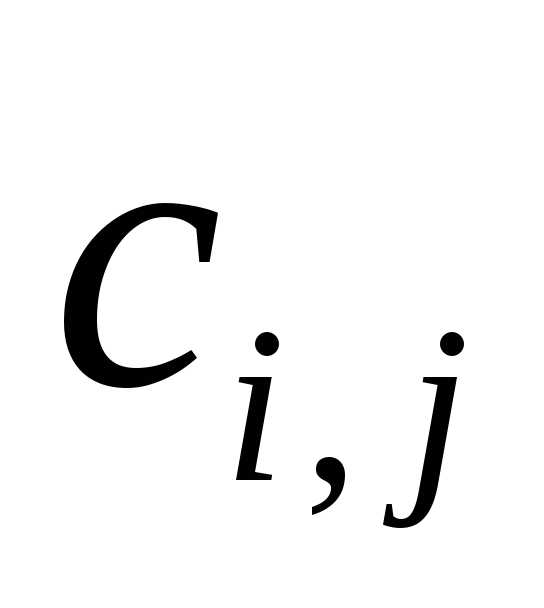 - затраты на
доставку единицы продукции из пункта
производства
- затраты на
доставку единицы продукции из пункта
производства
 в пункт потребления
в пункт потребления .
.
Считается, что каждый потребитель обслуживается одним предприятием. Целевая функция задачи – суммарные затраты на размещение предприятий и обслуживание спроса – должна достигнуть минимума. Простейшая задача размещения на сети записывается в виде
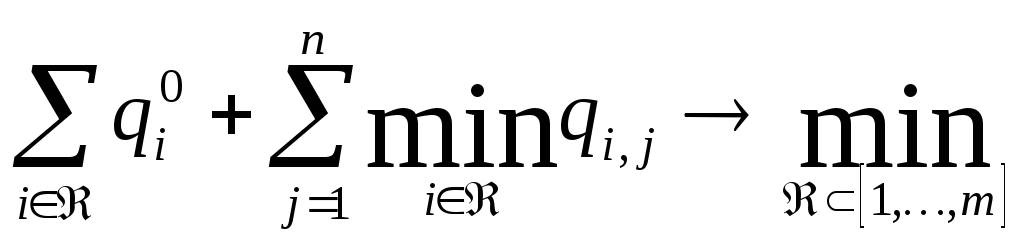 ,
,
где
![]() ,
,![]() ,
,![]() .
.
Простейшие задачи
размещения на сети относят к числу
трудноразрешаемых (сложность задач
дискретной оптимизации). Для некоторых
классов простейших задач размещения
на сети построены эффективные точные
алгоритмы. Наиболее известными являются
задачи со связанными и с квазивыпуклыми
матрицами (![]() ).
Матрица (
).
Матрица (![]() )
квазивыпукла, если для всяких
)
квазивыпукла, если для всяких![]() и
и![]() ,
,![]() .
.
Матрица (![]() )
связана, если для всяких
)
связана, если для всяких![]() ,
,![]() разность
разность![]() меняет
знак не более одного раза при монотонном
изменении
меняет
знак не более одного раза при монотонном
изменении![]() .
В общем случае для решения простейших
задач размещения на сети хорошо себя
зарекомендовали методы ветвей и границ.
Для простейших задач размещения на сети
играет важную роль при построении
математических методов решения
математической теории стандартизации
задачи.
.
В общем случае для решения простейших
задач размещения на сети хорошо себя
зарекомендовали методы ветвей и границ.
Для простейших задач размещения на сети
играет важную роль при построении
математических методов решения
математической теории стандартизации
задачи.
Для нелинейной
простейшей задачи размещения на сети
производственная функция
![]() - затраты на размещение предприятия
- затраты на размещение предприятия![]() зависят от суммарного объема спроса
зависят от суммарного объема спроса![]() ,
обслуженного из этого предприятия. В
случае кусочно-линейной, растущей,
вогнутой, производственной функции
нелинейная задача размещения сводится
к простейшей задаче размещения на сети.
,
обслуженного из этого предприятия. В
случае кусочно-линейной, растущей,
вогнутой, производственной функции
нелинейная задача размещения сводится
к простейшей задаче размещения на сети.
Задачи математической теории стандартизации возникают при обосновании типажа (оптимального ряда) машин, механизмов и оборудования, параметров новых технических изделий, состава систем технических средств и т.п. Задача имеет своей целью исключение нерационального многообразия видов, марок, моделей и типоразмеров производимой продукции для создания условий организации крупносерийного специализированного производства и внедрения в производство продукции с наилучшими технико-экономическими показателями. В качестве критерия выбора рациональной системы изделий (продукции), предназначенной для удовлетворения заданного спроса, часто используют минимум суммарных затрат в сферах проектирования (начальные затраты), производства и эксплуатации изделий.
Рассматривают также обратную задачу с критерием максимизации системы при ограничении на величину суммарных затрат. Различные постановки задачи позволяют учитывать такие факторы, как:
уменьшение удельных производственных затрат с увеличением серийности производства;
динамику производственных и эксплуатационных затрат;
ограничения на объемы производства;
динамику и случайность спроса.
С практической точки зрения интересны двухуровневые задачи стандартизации, где требуется выбирать элементы (компоненты, изделия, модули) первого уровня и элементы (компоненты, узлы) второго уровня. При этом спрос удовлетворяется с помощью выбранных элементов второго уровня.
При построении математических методов решения перечисленных задач важную роль играет простейшая задача размещения на сети.
К распределительным относятся такие широко распространенные задачи, как транспортная задача линейного программирования, задача о назначениях и многие другие.
Обозначим:
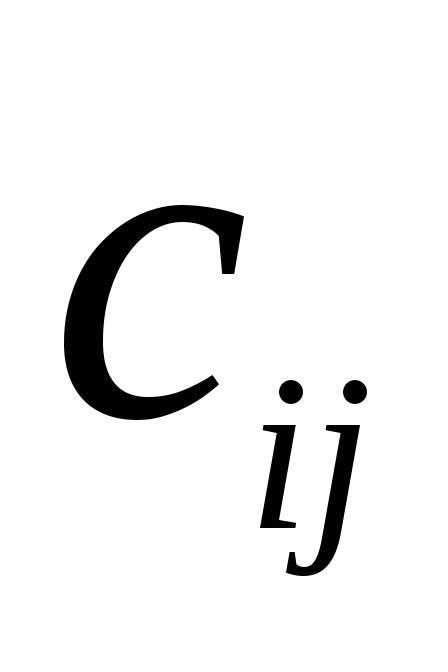 - затраты на
перевозку 1единицы однородного груза
вида
- затраты на
перевозку 1единицы однородного груза
вида
 к пункту
к пункту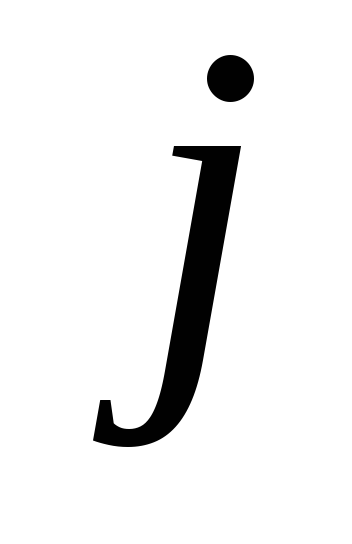 ,
,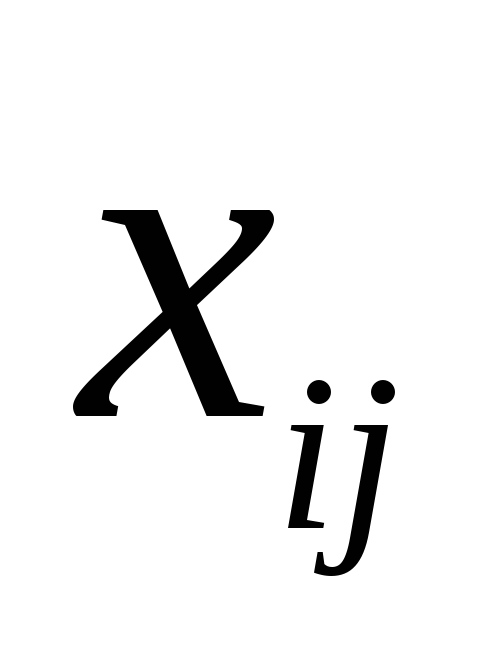 - количество этого
груза
- количество этого
груза
 к пункту
к пункту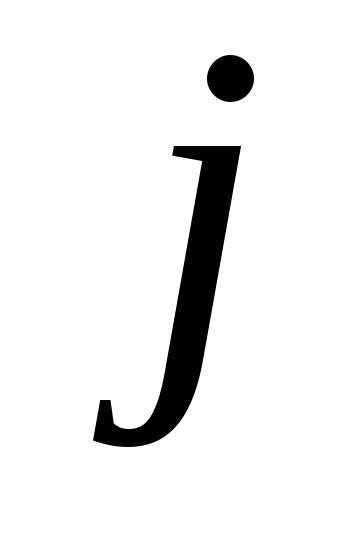 ,
,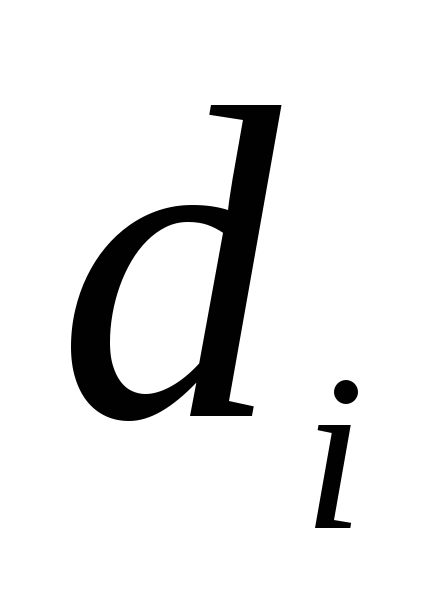 - располагаемое
количество груза вида
- располагаемое
количество груза вида
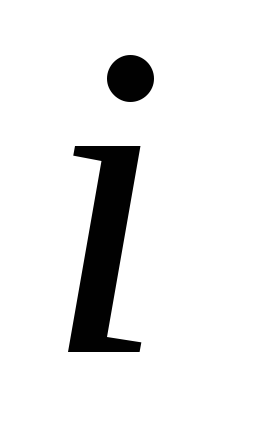 .
. - цена за единицу
груза вида
- цена за единицу
груза вида
 ;
;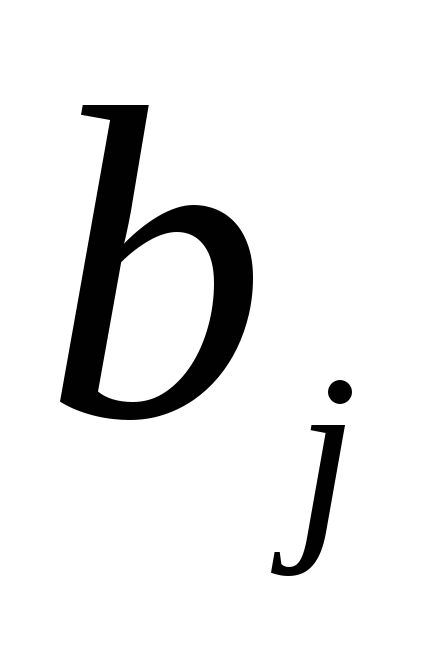 - объем продаж в
стоимостном выражении в пункте
- объем продаж в
стоимостном выражении в пункте
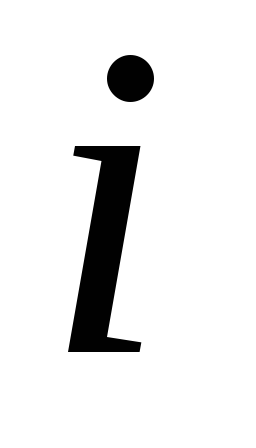 .
.
Задача заключается в составлении плана перевозок, обеспечивающего удовлетворение спроса во всех пунктах в этих грузах наиболее эффективным способом. Формально задача записывается так. Требуется найти минимум линейной формы
![]()
при выполнении условий
![]() ,
(5.1)
,
(5.1)
![]() ,
(5.2)
,
(5.2)
![]() .
(5.3.)
.
(5.3.)
Линейная форма
![]() определяет суммарные транспортные
издержки на перевозку грузов. Ограничения
(5.1) означают, что объем доставленного
в каждый пункт потребления груза должен
удовлетворять сложившийся там спрос.
Условия (5.2) означают, что количество,
направляемого во все пункты потребления
груза
определяет суммарные транспортные
издержки на перевозку грузов. Ограничения
(5.1) означают, что объем доставленного
в каждый пункт потребления груза должен
удовлетворять сложившийся там спрос.
Условия (5.2) означают, что количество,
направляемого во все пункты потребления
груза![]() ,
не должен превышать располагаемой
величины
,
не должен превышать располагаемой
величины![]() .
.
В распределительной задаче нередко возникает необходимость учитывать двусторонние ограничения на переменные модели. В терминах задачи, приведенной выше, двусторонние ограничения переменных могут истолковываться, например, как ограничения пропускных способностей коммуникаций и нецелесообразность перевозок недогруженным транспортом. В этом случае ограничения (5.3) примут вид
![]() (5.4.)
(5.4.)
Задача (5.1.)-(5.3.), (5.4.) называется распределительной задачей с двусторонними ограничениями.
Сам термин
распределительная задача, по видимому,
связан со следующей задачей распределения
![]() видов изделий между
видов изделий между![]() предприятиями.
предприятиями.
Задачи распределения могут решаться в статической (однократной) и в динамической постановке. В последнем случае часто применяют методы стохастического программирования, в которых принятие решений основано на вероятностных оценках будущих значений параметров.
Распределительные задачи, особенно линейные, получили распространение в практике, например в химической промышленности, и могут быть, в какой-то степени, основой оптимального управления производственными системами. Основной принцип моделирования распределительных задач рассмотрим на конкретном примере модели объемного распределения годовой производственной программы.
Постановка этой задачи заключается в определении годовой производственной программы и предполагает ее дальнейшее номенклатурно-количественное распределение во времени и пространстве с учетом выполнения необходимых ограничений и соответствующих технико-экономических показателей. Первой распределительной моделью в иерархии взаимосвязанных экономико-математических моделей производственного планирования является модель объемного распределения годовой производственной программы по периодам (например, кварталам). При этом должны учитываться следующие основные экономические условия (требования):
Безусловное выполнение общего задания по номенклатуре и объемам выпуска.
Соблюдение директивных сроков выпуска и сроков поставки по договорам.
Непрерывная загрузка основных групп рабочих мест и производственного оборудования в каждом квартале.
Равномерный выпуск продукции по стоимости.
Максимально возможная концентрация выпуска одноименных и конструктивно-однородных групп изделий.
Максимально возможная непрерывность производства и выпуска изделий каждого наименования.
