2. Задача максимизации выпуска в заданном ассортименте

Исторически первой задачей оптимального производственного планирования является задача максимизации выпуска в заданном ассортименте, которая была строго математически сформулирован отечественным математиком и экономистом Л. В. Канторовичем (1939 г.). Эта задача возникает, когда требуется распределить производственную мощность между выпуском нескольких видов продукции, потребности в которых задаются определенными соотношениями – ассортиментным набором, или комплектом.

Пусть имеет оборудование с фондом времени эксплуатации , используемое врежимах для выпускапродуктов. За 1 час работы в режимевыпускаетсяпродукта. Продукция комплектуется в ассортиментные наборы, причем один ассортиментный набор содержитпродукта(). Требуется так распределить время работы оборудования между различными режимами, чтобы количество укомплектованных ассортиментных наборов было максимальным. Обозначая,, затраты времени на работу в режимеи предполагая линейную зависимость выпуска каждого продукта от времени использования режимов, получаем задачу оптимизации:

, ; (2.1.)

; (2.2.)

, (2.3.)

где (2.1.) – условие неотрицательности времени использования каждого режима, (2.2.) – ограничении е на фонд времени эксплуатации, а запись функции цели (2.3.) основан на том, что при выпуске продукта в объемеможно укомплектовать самое большее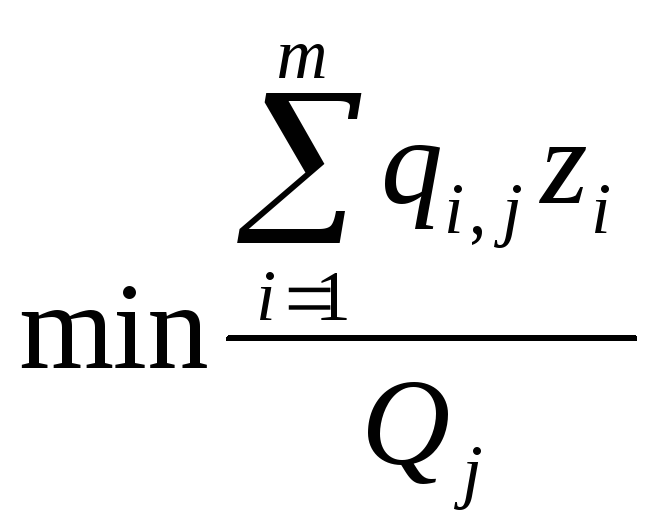ассортиментных наборов. Нестандартную форму функции цели (2.3.) можно преобразовать, если ввести обозначение для неизвестного количества ассортиментных наборов. Тогда вместо (2.3.) можно записать

(2.4.)

. (2.5.)

Задача линейного программирования (2.1.), (2.2.), (2.4.), (2.5.) эквивалентна (2.1.) – (2.3.). Кроме того, после элементарных преобразований она совпадает с задачей максимизирующего участника матричной игры. Для решения данной задачи пригоден любой численный метод линейного программирования, а также численный метод решения матричной игры.

Экономически функция цели (2.3.) при условиях (2.1.), (2.2.) или (2.5.) при условиях (2.1.), (2.2.), (2.4.) эквивалентна валовому выпуску с учетом специфического требования, что продукция нужна при жестких соотношениях между объемами по ее отдельным видам. Это требование может соответствовать характеру задач, решаемых на уровне предприятия. Условия линейности соотношения (2.4.) и представимости производственной мощности одним числом при этом, как правило, более стеснительны. Задача максимизации выпуска в заданном ассортименте иногда используются в макроэкономическом анализе. При этом с помощьюзадают желательную структуру конечного потребления,- обобщенная «производственная мощность» экономики в целом. Такая интерпретация может быть оправданной лишь в сугубо теоретических исследованиях.

3. Задача загрузки оборудования

Задача загрузки оборудования заключается в определении рациональной номенклатуры и объемов выпуска изделий в натуральном выражении при максимальном использовании оборудования в течение планового периода, как правило, года, на основе расчета производственной мощности предприятия. В задачах загрузки оборудования рассматриваются не все, а только ведущие (лимитирующие) группы оборудования. Под годовым, эффективным фондом времени одного станка из группы понимается число календарных суток за вычетом праздничных и выходных, а также времени, отводимого под планово-предупредительный ремонт (в часах при работе в одну смену). Для формализации задачи загрузки оборудования используют оптимизационные экономико-математические модели.

Базовая модель включает ограничения:

по спросу и заказам на продукцию предприятия

, (3.1.)

по мощности

, (3.2.)

на неотрицательность переменных

, (3.3.)

и критерии оптимизации:

на максимум загрузки оборудования

, (3.4.)

на максимум объема реализации продукции

, (3.5.)

на максимум прибыли

, (3.6.)

где - объем выпуска изделияв натуральном выражении;

- номера изделий, входящих в номенклатуру предприятия;

- номера групп оборудования;

- число изделий в заказе ;

- объем спроса на изделие;

- норма затрат времени группы оборудования на обработку единицы изделия(станко-часы);

- годовой эффективный фонд времени работы группы оборудования (часы);

- цена за изделие ;

- переменные издержки.

Решение модели возможно как однокритериальной при любой целевой функции (3.4. - 3.6.) либо как многокритериальной с использованием всех (или некоторых двух) из этих целевых функций (векторная оптимизация). Необходимо помнить, что задача формулируется с линейными ограничениями, поэтому все коэффициенты при переменных должны быть независимыми от их значений.

Усложнение задачи идет за счет дополнительного предположения, что в плановом году будет ввод нового оборудования, и учета производствен –технологической структуры предприятия. Тогда можно сформулировать две модификации модели (3.1.- 3.6.). В первом случае при сохранении ограничений (3.1.) и (3.3.) трансформируются ограничения по мощности:

, , (3.7.)

вводятся дополнительные ограничения по инвестициям:

, (3.8.)

и на неотрицательность новых переменных:

, , (3.9.)

критерии (3.4.) и (3.5.) сохраняются, а (3.6.) приобретает вид

, (3.10.)

где - искомое дополнительное количество единиц оборудования в группе;

- годовой эффективный фонд времени работы единицы оборудования из группы ;

- цена единицы оборудования группы ;

- годовой фонд инвестиций в оборудование.

Во втором случае, как и в базовой модели, фонд времени эксплуатации оборудования считается заданным, но учитываются различные технологические способы его использования, так что в качестве переменных выступают не объемы выпуска каждого изделия, а объемы использования технологических способов, соответственно изменяются ограничения и критерии (3.1. - 3.6.). Например, ограничение (3.1.) по спросу и заказам на продукцию предприятия принимает вид:

, (3.11.)

где - время использования технологического способана оборудовании вида;

- норма выпуска изделия за единицу времени при технологическом способе,.

Если эту модель решать как переменную, то может оказаться, что производство одного и того же изделия предусмотрено несколькими технологическими способами. На некоторых предприятиях это недопустимо или нежелательно, тогда целесообразно модифицировать ее в целочисленную.