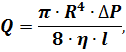Приведём пример оформления решения задачи.
2.51. Определите высоту над постелью больного, на которой висела капельница. Если в вену предплечья вводился раствор лекарственных веществ. Плотность раствора 1026 кг/м3, вязкость 1,8 мПа×с, давление в вене составляло 60 мм водного столба. Игла, введенная в вену, имела диаметр просвета равный 0,6 мм, длину 40 мм. Через капельницу в венозное русло больного поступило 500 мл раствора за 45 минут.
Решение
|
|
Указание на ламинарный режим течения интерпретируем, как возможность использовать для решения формулу Пуазейля:
Из
формулы Пуазейля получим выражение
для разности давлений ∆P:
Отдадим себе отчёт в том, что разность давлений в данном случае обусловлена разностью гидростатического давления и давления в вене: ∆P = ρ·g·h - Pвен. Получим выражение для высоты капельницы над постелью больного:
|
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
h -? |
.
.
В правую часть расчётной формулы вместо обозначений физических величин подставим обозначения единиц этих величин в СИ, произведём над ними необходимые действия и убедимся, что полученное в результате обозначение единицы соответствует искомой величине.
Расчётная формула даёт единицу искомой величины.
Подставим в получившееся выражение числовые данные и получим окончательный результат, используя единицы СИ:
.
Полученное в результате решения число вполне правдоподобно.
3. Колебания и волны, биоакустика
3.1. Маятник совершает гармонические колебания по закону косинуса. Определите начальную фазу колебаний в градусах, если начало отсчета времени совпало с моментом прохождения маятником положения максимального отклонения от положения равновесия.
3.2. Маятник совершает гармонические колебания по закону косинуса. Определите начальную фазу колебаний в градусах, если начало отсчета времени совпало с моментом прохождения маятником положения равновесия.
3.3. Колебательное движение материальной точки задано законом:
x = 12• SIN(0,63•t + 0,5)
Определите максимальное ускорение колеблющейся точки.
x - в миллиметрах, t - в секундах.
3.4. В механической системе совершаются собственные гармонические колебания с частотой 46 Гц и амплитудой 2 мм. Определите частоту гармонических колебаний в системе после того, как амплитуда увеличилась на 0,5%.
3.5. Два камертона звучат одновременно. Частота колебаний одного из них 6000 Гц, другого 6003 Гц. Определите частоту изменения амплитуды результирующего колебания.
3.6. Два камертона звучат одновременно. Частота колебаний одного из них 3000 Гц, другого 3005 Гц. Определите период изменения амплитуды результирующего колебания.
3.7. Определите период собственных гармонических колебаний груза массы 4 кг, подвешенного вертикально на пружине с жесткостью 72 Н/м.
3.8. Определите частоту второй гармоники в гармоническом спектре нормальной ЭКГ, если частота сердечных сокращений (ЧСС) составляла 66 сокращений в минуту.
3.9. Определите частоту собственных гармонических колебаний груза массы 4 кг, подвешенного вертикально на пружине с жесткостью 60 Н/м.
3.10. Определите круговую частоту собственных гармонических колебаний груза массы 5 кг, подвешенного вертикально на пружине с жесткостью 77 Н/м.
3.11. Гармонические колебания материальной точки массой 5 г происходят по закону:
X= 1• cos( 77• t + 12). Определите частоту изменения потенциальной энергии колебаний.
t - в секундах; x - в миллиметрах.
3.12. Гармонические колебания материальной точки массой 4 г происходят по закону:
X= 6•cos( 66• t+12).
Определите частоту изменения кинетической энергии колебаний.
(t - в секундах; x - в миллиметрах).
3.13. Гармонические колебания материальной точки массой 2 г происходят по закону:
X= 5cos( 67t +12). Определите период изменения потенциальной энергии колебаний.
t - в секундах; x - в миллиметрах.
3.14. Гармонические колебания материальной точки массой 3 г происходят по закону:
X= 3cos( 66t +12). Определите период изменения кинетической энергии колебаний.
(t - в секундах; x - в миллиметрах).
3.15. Гармонические колебания материальной точки массой 7 г происходят по закону: x= 1cos( 27t +12). Определите круговую частоту изменения потенциальной энергии колебаний. (t - в секундах; x - в миллиметрах).
3.16. Гармонические колебания материальной точки массой 1 г происходят по закону: x = 3cos( 68t +12). Определите круговую частоту изменения кинетической энергии колебаний.
(t - в секундах; x - в миллиметрах).