
matan1
.pdf
1. Множества. действия с множествами.
Определение: множествосовокупность объектов, обозначаемая большими буквами A, B, X, C; элементы маленькими a,b,x,c.Элементы а принадлежащие множеству A. a A.не
принадлежит a A. B A-все элементы множества В принадлежит множеству А(В-подмножество множества А). Если множество А содержит n элементов, то она имеет 2n подмножества. Действия над множествами: U- объединение (сумма); /разность; -пересечение (произведение). Определение: Объединение множеств А и В называется такое множество С , которое состоит как из элементов множества А, так и из элементов множества В. Пересечение множеств А и В наз. такое множество С, которое состоит только из тех элементов, которые одновременно принадлежат множеству А и В. Разность множеств А и В называется множество С, которое состоит из элементов множества А, которые не входят в множество В:А\В=С . Множество, состоящее из конечного числа элементов называется конечным. Множества А и В называются эквивалентными, если известны взаимноодназначные соответствия между их элементами. Если каждый элемент множества можно перенумеровать-то множество счетно. Множество, эквивалентное множеству натуральных чисел, называется счетным. Счетное множество называется последовательность и обозначается { xn }.
М={2*n}-натуральные четные числа. {2*n-1}- натуральные нечетные числа.
Множество рациональных число - счетно, иррациональных - несчетно. Часто Счетные множества задаются с помощью формулы общего члена. Иногда последовательность задается рекуррентно.
2. Последовательность. Примеры. Предел последовательности.
Пусть каждому натуральному n поставлено в соответствие число
x |
n |
|
1 x1
…….. n xn
Тогда говорят, что задана последовательность
следует за |
xm . |
x |
n |
|
|
x |
n |
n 1 |
|
если n>m, то xn
xn 1 следует за
аргумента: |
|
x |
n |
|
|
f x |
|
(можно дать определение последовательности , как функции от натурального
, an f (n) )
Примеры. |
|
|
|
|
|||||
1. |
x |
6n 7 |
|
x 1 |
|
x 5 |
|
||
n 4 |
5 |
6 |
|||||||
|
n |
|
1 |
2 |
|||||
|
|
|
|
|
|
||||
|
xn |
2 |
|
|
|
|
|
||
2. |
1 принимает два значения +-1 |
||||||||
3. |
xn |
=sin(n)-ограниченная. |
|
|
|||||
Если для n<m |
|
|
|
|
|||||
а) xn |
xm -последовательность возрастающая. |
||||||||
б) xn |
xm -последовательность называется неубывающей. |
||||||||
с) xn |
xm -последовательность называется убывающей. |
||||||||
д) xn xm -последовательность называется невозрастающей. а- д - монотонные последовательности.
Если nxn a , то последовательность стационарная. xn =sin(n)-немонотонная.
1

Определение: Числа а называется пределом последовательности { xn |
}, если для любого |
положительного числа найдется номер N ( ) , такой, что xn a |
, как только n N |
0N( ) : n N( ) xn a , для любого положительного найдется номер n от |
|
что для любого n> N ( ) следует неравенство. |
|
Примеры.
Доказать, что |
lim |
1 |
=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0N ( ) : n |
N ( ) |
|
1 |
0 |
|
|
|
1 |
|
|
|
1 |
|
||||||
|
|
|
|
||||||||||||||||
|
n |
|
|
n |
|
|
n |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
доказать, что |
lim |
1 |
=0 означает, что нужно найти |
N ( |
|||||||||||||||
n |
|||||||||||||||||||
|
|||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример2. Доказать |
q^n=0 |q|<1. |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1) |
если q=0, то утверждение очевидно. |
||||||||||||||||||
2) |
Q не равно 0, то |
|
|
|
|
|
|
|
|
||||||||||
0N ( ) : n N ( ) q |
n |
0 q |
n |
n lg |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Геометрический смысл предела последовательности.
0N( ) : n N( ) x |
n |
a x |
n |
a |
|
|
|
НАЧЕРТИТЬ ОСЬ
Отметим на числовой оси точки a, a- ,a+
n 1 ) .
| q | log n |
lg | | |
|
lg | q | |
||
|
a x |
n |
a |
|
|
,такой,
x |
N ( ) |
-лежит точно вне окрестности. То, что число а является пределом последовательности |
|||
|
|||||
|
|
||||
{ xn |
} означает, что в окрестности точки |
|
|
|
|
а лежат все члены последовательности { xn |
}, начиная с номера |
N( ) 1Где лежат |
x1 , x2 ,… xN ( ) |
||
-
неизвестно(нам это и ненужно. Говорят, что существование предела последовательности не зависит от первых членов последовательности)
Пример.
lim |
3n 1 |
3 |
|
|
|
|
|||||||
n |
4 |
|
|
|
|
||||||||
n |
|
|
|
|
|
|
|||||||
N ( ) |
|
11 4 |
1 |
0< <11/4 |
|||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
|
|
|
|
>11/4 |
|||
1) |
|
=4 в окрестности точки 3 расположены все члены последовательности. |
|||||||||||
2) |
|
=1 в окрестности точки 3 расположены все члены последовательности начиная с |
|||||||||||
N (1) |
11 4 |
1 8 |
|||||||||||
|
1 |
|
|||||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
3) |
|
=1/2 в окрестности точки 3 расположены все члены последовательности начиная с |
|||||||||||
N (1/ 2) |
|
11 2 |
1 19 |
||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
1/ 2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
Мы можем x1 , x2 ,…. x18 посл. Рассмотреть, где они лежат.
2

Если последовательность имеет предел, то она сходящаяся, если предела нет, то расходящаяся.
4. Единственность предела последовательности.
Теорема 1. Если последовательность { xn |
} имеет предел, то он единственный. |
|||||||||||||||||||||||
Док-во. Предположим, что последовательность{ xn } |
имеет2 предела: |
|
|
|||||||||||||||||||||
Тогда lim xn |
= a |
|
|
|
|
lim |
xn |
=b |
|
|
|
|
|
|
|
|
|
|
||||||
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И пусть a<b для определенности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пусть |
|
|
b a |
>0, тогда для |
b a |
найдется N ( ) : xn |
a |
b a |
и |
|||||||||||||||
3 |
|
|
3 |
3 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
xn b |
b a |
или a |
b a |
xn |
a |
b a |
, b |
|
b a |
xn b |
b a |
или |
||||||||||||
|
3 |
3 |
3 |
3 |
|
|
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4a b |
xn |
2a b |
, |
2b 3 |
xn |
|
4b a |
,но |
2b 3 |
|
2b a |
, т.к. a<b,поэтому начиная с номера |
||||||||||||
3 |
|
3 |
|
3 |
3 |
|
|
3 |
3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
N 1 |
все члены последовательности лежат в двух непересекающихся интервалах.(ТУТ ДОЛЖЕН |
|||||||||||||||||||||||
БЫТЬ РИСУНОК)
Получаем противоречие следовательно наше предположение не верно.
Билет 5. Ограниченные последовательности. Ограниченность сходящейся последовательности. Пример.
Определение 1. последовательность {
k 0 : x |
n |
k n |
|
|
x |
n |
|
} называется ограниченной, если существует
Опр2. Последовательность { xn } называется ограниченной, если
Эти два определения эквиваленты.
Т2 Если последовательность сходится, то она ограничена. Доказательство.
m, n : m x |
n |
M n |
|
|
Пусть
lim n
x |
n |
|
= a
это означает, что
0N( ) : n N( ) x |
n |
a |
|
|
Возьмем =1, тогда для всех |
n N(1) : |
xn |
a 1 или a 1 xn |
a 1. Через |
|||||||||
K обозначим max(|a-1|,|a+1|, |
x |
|
, x |
2 |
, x |
N (1) |
) |
|
|||||
|
|
1 |
|
|
|
|
|
||||||
|
xn |
|
|
k , т.е. последовательность ограничена. |
|||||||||
Тогда для n выполняется неравенство |
|
|
|||||||||||
Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
1). |
xn sin n -ограниченная |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
2) |
xn 1 -ограниченная |
1-2-предела не имеют. |
|
||||||||||
3) |
xn |
4) |
xn |
5) |
xn |
6) |
xn |
|
3n 2 |
-ограниченная последовательность. |
||||
n |
4 |
|||||
|
|
|||||
n |
2 |
-ограничена снизу |
||||
|
||||||
n2 -ограничена сверху |
||||||
|
1 |
|
-ограничена 0 1 n 1 |
|||
|
|
n |
|
|
||
6. Бесконечные последовательности. Бесконечно большие последовательности. Примеры. Связь между бесконечно большими и бесконечно малыми последовательностями.
3

Опр1. Последовательность { xn |
} называется б.б, если k 0N(k) : n N(k) xn |
k |
при этом |
|||||
пишут, что lim xn = |
|
|
|
|
|
|
||
|
|
x |
|
|
|
|
|
|
Если все члены последовательности, начиняя с некоторого номера положительные, то пишут |
|
|||||||
lim |
xn =+ ,отрицательные lim |
xn =- . |
|
|
|
|||
n |
|
n |
|
|
|
|
||
xn |
|
n |
|
|
|
|
|
|
= |
1 n -бесконечно большая последовательность. |
|
|
|
||||
yn |
n lim yn =+ |
zn n |
lim zn =- . |
|
|
|
||
|
|
n |
|
|
n |
|
|
|
Опр2. Последовательность { n } называется бесконечно малой, если lim xn =0 или |
|
|
|
|||||
|
|
|
|
|
n |
|
|
|
0N( ) : n N( ) n |
. |
|
|
|
||||
Теорема. |
|
|
|
|
|
|
||
Если последовательность { xn |
} бесконечно большая, то последовательность {1/ xn }-бесконечно |
|||||||
малая и наоборот. Если последовательность { n }-бесконечно малая, то последовательность {1/ |
n |
|||||||
бесконечно большая. |
|
|
|
|
|
|
||
Доказательство. |
|
|
|
|
|
|
||
}-
1) |
|
2) |
|
1 |
|
x |
n |
|
|
1
{xn }-б.б k 0N(k
{xn }-бесконечно малая.
.Возьмем k |
1 |
. Нашли N( )=N( |
|
|
|||
|
|
) : n |
||
|
||
1 |
) k |
|
k |
||
|
||
N(k)
0N(
N ( 1 ) k
xn |
|
k или |
) : n N( ) |
||
1 |
k . |
|
x |
|
|
n |
|
|
|
|
|
1 |
|
x |
n |
|
|
|
|
|
1 |
.Возьмем |
||
k |
||||
|
|
|
||
xn |
|
или |
||
1 k
.
Пример 1. |
xn = x |
2 |
-бесконечно большая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
k 0N(k) : n N(k) |
|
|
|
n |
2 |
|
|
k n |
2 |
k n |
|
|
k N(k) [ |
k ] 1 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 2. |
xn = |
-бесконечно малая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0N ( ) : n N ( ) |
|
|
1 |
|
|
|
|
|
1 |
n |
2 |
|
1 |
n |
1 |
N ( ) |
|
1 |
|
|
1 |
|
||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
7. Свойства бесконечно малых последовательностей. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1. |
|
|
|
|
|
|
|
|
|
Если последовательность { n } и { |
n |
}- бесконечно малые, то последовательность |
||||||||||||||||||||||||||||
{ n |
n |
}-бесконечно малая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Док. { n } и { n |
|
}-бесконечно малые, |
т.е. 0 N1 ( ) : n N1 ( ) n |
2 |
, |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 N2 |
( ) : n N2 ( ) n |
|
|
. Пусть N ( ) max( N1 , N2 ) , тогда для |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n> N( ) n |
|
|
|
2 и n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
n |
|
n |
|
n |
|
n |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 N( ) : n N( ) n |
|
|
n |
.Т.е. { n |
n }-бесконечно малая |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
последовательность.(алгебраическая сумма бесконечно малых последовательностей, есть |
|
|||||||||||||||||||||||||||||||||||||||
бесконечно малая последовательность). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2. |
|
|
|
|
|
|
|
|
|
Если последовательность { n }-бесконечно малая, а последовательность { xn |
}- |
|||||||||||||||||||||||||||||
ограниченная, то последовательность { n xn }-бесконечно малая.(произведение бесконечно малой
последовательности на ограниченную, есть бесконечно малая последовательность). Доказательство.
4

{ xn }-огр. k 0 : n xn k |
.{ n }-бесконечно малая 0N( ) : n N( ) n |
тогда | n xn |= | n | | xn | k |
k , т.о. имеем |
0N( ) : n N( ) n xn ,т.е. { n xn }-бесконечно малая последовательность. |
|
3.Если последовательность { n |
}-бесконечно малая, то она ограничена. |
|
k |
,
Доказательство.
Т.К последовательность {
|
n |
|
}-бесконечно малая, то
lim n
|
n |
|
=0, т.е. последовательность является
сходящейся.Всякая сходящаяся последовательность ограничена(теорема). |
|
|
|
|
|
|
||||||||||||||||||||||||||
4.Если последовательности { |
n |
} и { n }-бесконечно малые, то последовательность { n n }- |
|
|||||||||||||||||||||||||||||
бесконечно малая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
последовательность { n }-бесконечно малая, согласно свойству 3 она ограничена. Применяем |
|
|||||||||||||||||||||||||||||||
свойство 2 к ограниченной последовательности { n |
} и б.м посл. { n }, получаем, что |
|
|
|||||||||||||||||||||||||||||
последовательность n n -бесконечно малая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
5.Если последовательность { n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||||||||
}-бесконечно малая, то последовательность |
|
-бесконечно |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
большая. И наоборот. Если последовательность { n |
}-бесконечно большая, то последовательность |
|||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-бесконечно малая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1) { n |
}-бесконечно малая. 0N( ) : n N( ) |
|
n |
|
или |
1 |
|
1 |
.Возьмем k |
1 |
. |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нашли N( )=N( |
1 |
) k N ( |
1 |
) |
1 |
k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возьмем k |
1 |
что и требовалось доказать. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) { |
|
}-б.б k 0 N(k) : n N(k) |
|
k |
или |
1 |
|
1 |
.Возьмем |
1 . |
|
|
||||||||||||||||||||
n |
n |
n |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
k |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6.Теорема о связи сходящихся и бесконечно малых последовательностей. |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Если последовательность { xn } сходится к числу a, то последовательность n |
xn a - бесконечно |
||||||||||||||||||||||||||||||
малая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для того, чтобы число а было пределом последовательности xn необходимо и достаточно |
|
|
||||||||||||||||||||||||||||||
n |
xn |
a была бесконечно малая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Доказательство (необходимости). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1) |
|
|
|
|
|
Пусть lim |
xn |
=а-это означает, 0N( ) : n N( ) xn |
a . Обозначим |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn a n , получим 0N( ) : n N( ) |
|
n |
|
, т.е |
|
|
|
||||
2) |
Достаточность. |
|
|
||
Пусть последовательность n xn a -б.м.-это означает, | xn a | , т.о имеем 0N( ) : n N( )  xn a
xn a
8. Ограниченность бесконечно малой последовательности.
{ n }-б.м.п.
0N( ) : n N( ) |
n |
|
|
|
lim |
xn |
=а. |
n |
|
|
или
???
5

9. Связь между сходящимися и бесконечно малыми последовательностями. |
|
|
|
|
Теорема о связи сходящихся и бесконечно малых последовательностей. |
|
|
|
|
Если последовательность { xn } сходится к числу a, то последовательность n |
xn |
a - бесконечно |
||
малая. |
|
|
|
|
Для того, чтобы число а было пределом последовательности xn необходимо и достаточно |
|
|||
n xn a была бесконечно малая. |
|
|
|
|
Доказательство (необходимости). |
|
|
|
|
1)Пусть lim xn =а-это означает, 0N( ) : n N( ) xn a . Обозначим |
xn a n |
, |
||
n |
|
|
|
|
получим 0N( ) : n N( ) n , т.е { n }-б.м.п. |
|
|
|
|
2)Достаточность. |
|
|
|
|
Пусть последовательность n xn a -б.м.-это означает, 0 N( ) : n N( ) n |
или |
|||
| xn |
a | , т.о имеем 0N( ) : n N( ) xn |
a lim |
xn =а. |
|
|
|
n |
|
|
10. Арифметические свойства сходящихся последовательностей. Предел суммы, произведения, частного двух сходящихся последовательностей.
- предел суммы: если последовательности {xn} и {yn} сходящиеся и lim xn |
a , lim yn |
b конечно, |
n |
n |
|
то lim{xn |
yn } a b |
|
n |
- предел произведения: если последовательности {xn} и {yn} сходящиеся и
lim x |
n |
|
|
n |
|
a
,
lim yn |
b конечно, то lim{xn yn } a b |
n |
n |
- предел частного: если последовательности {xn} и {yn} сходящиеся и
lim x |
n |
|
|
n |
|
a
,
lim y |
n |
|
|
n |
|
b
конечно,
то имеем |
x |
n |
|
a |
n |
т.е. это означает, что |
lim |
x |
n |
|
a |
|
|
|
|
||||||||
y |
|
b |
y |
|
b |
||||||
|
n |
|
|
|
n |
n |
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Замечание 1:
U(ε,a) – ε-окрестность точки a (a-ε ; a+ ε). U(ε,∞) – ε-окрестность точки x {x: {|x|>ε) U(ε,+∞) – ε-окрестность точки +∞ {x: {|x|>ε) U(ε,-∞) – ε-окрестность точки -∞ {x: {|x|<ε) Тогда определение предела можно переписать:
lim x |
n |
a |
n |
|
|
|
|
0 N( ) : n N( ) xn U ( ; )
Здесь a конечно или бесконечно.
Замечание 2:
Если последовательности имеют бесконечные пределы, то теоремы неверны.
11. Предельный переход в неравенствах. |
|
|
|
|
|
Теорема 1: Если, начиная с некоторого номера an bn |
cn и lim an |
lim cn |
a , то lim bn |
a . |
|
|
|
n |
n |
n |
|
6

Доказательство: 0N1 ( ) : n N1 |
( ) | an |
a | , 0N2 ( ) : n |
||||
N( ) max( N1 ( ), N2 ( )) , то тогда для |
n N ( ) |
a a |
n |
a |
или |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
a c |
n |
a |
|
|
|
|
|
|
|
|
N a
2(
) |
c |
n |
|
|
||
a |
n |
|
|
|
|
a |
bn
Пусть
c |
n |
a |
|
|
,
а это означает, что |
lim bn |
a |
n |
|
|
|
|
|
|
|
|
Теорема 2: Если lim a |
n |
a |
и a<b (a>c), то n |
(n |
) : n n |
a |
n |
|
|
|
b |
c |
b |
|
|
||
n |
|
|
|
|
|
|
|
|
Доказательство: lim an |
a 0N( ) : n N( ) | an |
a | |
||||||
n |
|
|
|
|
|
|
|
|
случае b a 0 , во втором a c 0 |
|
|
|
|
|
|||
Теорема 3: Если lim an |
a |
an b (an c) , то |
a b (a c) |
|
|
|||
n |
|
|
|
|
|
|
|
|
b(n
или
a
nc
a |
n |
|
|
|
|
|
|
a |
n |
|
|
c)
a
. В первом
Доказательство: Предположим, что a<b, но тогда, по Теореме 2 было бы an<b – противоречие.
12. Монотонные последовательности. Примеры. Предел монотонной ограниченной последовательности (без доказательства).
Определение: Последовательность xn называется неубывающей (невозрастающей), если
n |
x |
n |
x |
n 1 |
|
|
|
(x |
n |
|
x |
n 1 |
) |
|
|
. Если неравенства строгие, то соответствующая последовательность
называется возрастающей (убывающей). Эти последовательности называют монотонными.
Примеры:
1. xn |
|
1 |
. |
xn 1 |
|
n |
|||||
|
|
|
|
||
2. xn |
|
|
n |
. |
|
|
|
||||
|
|
n 1 |
|||
x |
n |
|
n |
|
|
|
|
||
|
|
|
|
|
x |
n 1 |
x |
n |
|
|
|
|||
1
1
1n n 1
n 2
n
1 n(n
1
1) (n
0 |
т.е. |
|
1 |
1)(n |
|
x |
n 1 |
|
|
|
|
||
2) |
0 |
||
|
|
||
xn – последовательность убывающая. xn 1 xn т.е. последовательность
возрастающая
Теорема (предел монотонной ограниченной последовательности): Всякая ограниченная снизу (сверху) убывающая (возрастающая) последовательность имеет предел.
Впримере №1:
Впримере №2:
x x
n
n
1 n
n
0 |
- ограничена снизу lim xn |
0 |
|
|||||
|
|
|
|
|
n |
|
|
|
n |
1 |
1 |
1 |
- ограничена сверху lim xn |
1 |
|||
1 |
n 1 |
|||||||
|
|
|
|
n |
|
|||
Данную теорему можно сформулировать по-другому: для того, чтобы возрастающая (убывающая) последовательность имела предел необходимо и достаточно, чтобы она была ограничена сверху (снизу)
13. Принцип вложенных отрезков.
Теорема: Для каждой системы вложенных отрезков, длина которых →0 существует хотя бы одна точка, принадлежащая всем отрезкам.
Доказательство: [a,b] [a1 ,b1 ] [a2 ,b2 ] ... [an ,bn ]
a a1 a2 an bn b2 b1 b
a a1 a2 ... an bn bn 1 ... b2 b1 b ,
{an} – последовательность левых концов отрезков, она возрастает и
n an b (ог раничена сверху ) lim an
n
7

{bn} – последовательность правых концов отрезков, она убывает и
n b |
a (ог раничена |
снизу) lim b |
|
|
|
|
|
|||
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
Пусть |
lim an |
c1 , lim bn |
|
c2 , lim an |
bn |
c1 |
c2 |
; по условию lim |
| bn |
an | 0 => |
|
n |
n |
|
n |
|
|
|
n |
|
|
c2 c1 |
0 c1 c2 c |
. Точки c принадлежат всем отрезкам, т.к. |
an |
c bn n |
||||||
14. Число e
см. 24 вопрос
15. Подпоследовательности. Предельная точка последовательности. Теорема БольцаноВейерштрасса
Определение: Точка a называется предельной точкой полседовательности {xn}, если
Подпоследовательность {xnn}: lim xnn a n
Теорема (Больцано-Вейерштрасса): Из любой ограниченной последовательности можно выделить сходящююся подпоследовательность.
Доказательство: Т.к. последовательность {xn} ограничена, то a,b : a xnn b n таким образом, мы имеем отрезок [a,b], содержащий все точки последовательности. Разделим [a,b] пополам точкой
|
|
a |
b |
|
|
|
|
|
|
l1 |
1 |
1 |
. Через [a2,b2] обозначим ту часть, которая содержит бесконечное число членов и т.д. |
||||||
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
Получим систему вложенных отрезков: [a; b] > [a1; b1] > [a2; b2] > … > [an;bn]. b |
a |
|
|
b a |
0 |
||||
n |
|
||||||||
|
|
|
|
n |
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
длина отрезка → 0 => c : an |
c bn |
. Выберем: на отрезке [a1, b1] точку x1n на отрезке [a2, b2] точку |
x2n, покажем, что {xnn} имеет предел: по выбору {xnn} an≤xnn≤bn. lim an |
lim bn c c по теореме о |
|||||
|
|
|
|
n |
n |
|
сложной переменной: lim xnn c . Таким образом, {xnn} - искомая подпоследовательность. |
||||||
n |
|
|
|
|
|
|
|
||||||
16. Фундаментальные последовательности. Критерий Коши (доказательство необходимости). |
|
|||||
Определение: {xn} называют фундаментальной последовательностью, если |
||||||
0N( ) : n, m N( ) | x |
n |
x |
m |
| |
|
|
|
|
|
|
|
||
(
0N( ) : n N( ),
p | x |
n p |
|
x |
n |
|
|
)
Критерий Коши: Для того чтобы последовательность была сходящейся, необходимо и достаточно, чтобы она была фундоментальной.
Доказательство необходимости: Пусть последовательность {xn} сходится к числу a ( a lim xn ). Это
n
значит, что 0 N ( ) : n N ( ) | x |
n |
a | |
пусть m>n, тогда |
||||
|
|
|
2 |
|
|
||
|
|
|
|
|
|
||
| xm xn | | xm a (xn a) | | xm a | | xn a | |
|
|
|
, т.е. {xn}-фундаментальная |
|||
2 |
2 |
||||||
|
|
|
|
|
|||
последовательность
17.Понятие функции. Способы задания функции. Сложные функции. Обратные функции.
Функция-это соответсвие. Пусть заданы два множества X и Y ,и каждому элементу множества X поставлен в соответствие элемент множества Y.При этом каждому элементу мн-ва Y соответствует хотя бы один элемент мн-ва X. Это соответствие называется функцией.
8

Если y=f(x), то x называется аргументом (независимая величина), y наз. функцией (зависимая величина).Понятие функции эквивалентно понятию соответствия. Пусть -подмножество,
через f(x)={y :y=f(x),x<E}-образ мн-ва E.
D Y подмножество, x : x X : f (x) D f (D) -прообраз D.Вообще говоря,
f(x)
: f (x) илиf (x)
.
Если каждому значению x соответствует единственное значение f(x), то функция называется однозначной.
Если множество значений {y} элементов x функции f(x)=y состоит более чем из одного элемента,то функция наз многозначной.
Мы будем рассматривать числовые функции:x и y-числовые множества. Для функций определены операции:
1.умножение на число :cf(x)
2.сумма f(x)+g(x)
3.произведение f(x)*g(x)
4.частное f(x)/g(x) если g(x) 0.
Числовая функция f(x) наз ограниченной сверху,если множество ее значений ограничено сверху.Числовая функция f(x) наз ограниченной снизу,если множество ее значений ограничено снизу.Ограниченная функция-ограничееная сверху и снизу.
Пусть на мн-ве
прообраз Y. |
f |
1 |
|
X определена функция y=f(x) и Y мн-во ее значений обозначим через
(Y ) {x : x X : f (x) y}
f
1 |
( y) |
|
-
Мы можем рассматривать функцию
f
1 |
( y) |
|
,заданную на
f |
1 |
(Y ) |
|
со значением в X,т е говорят,что
задана обратная функция.
Пусть заданы две функции y=f(x) и z=F(y) примем область значений функции y=f(x) содержится в области определения функции F(y) (в широком смысле либо как подмножество,либо совпадающие), тогда говорят,что задана сложная функция z=F(f(x)).
Способы задания 1.аналитический(с помощью формулы).Область определения-область тех значений,где формула имеет смысл.
2.графический(если дана функция y=f(x),то мн-во точек на плоскости с координатами (x,f(x)) называется графиком функции)
3.табличный(в таблице заданы значения аргументов и соответствующие значения функции) Элементарные функции Всякая функция,которая может быть получена с помощью конечного числа операций из основных
элементарнх функций ,наз элементарной функцией.
Операции:
, , |
n |
, |
|
|
n
,\,суперпозиция.F(f2(f3(x))).
Основные элементарные фнкции
1.Многочлен
P (x) a |
|
a x ... a |
|
x |
n |
0 |
n |
|
|||
n |
1 |
|
|
2Рациональные R(x)=Pn(x)/Qc(x)-отношение многочленов
3.Иррациональные(заданы с помощью суперпозиции конецного числа рациональной степени) y= 3 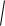 x 4
x 4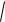 (x2 7)
(x2 7)
4Трансцендентные (показательные,логарифмические,тригонометрические).
18.Первое определение предела функции.Второе определение.Их эквивалентность.
Пусть функция f(x) задана на интервале (a,b) за исключением,быть может,точки Определение 1:
x |
0 |
|
.
9

Число |
a |
|
наз |
пределом |
|
функции |
f(x) |
в |
точке |
x0 |
,усли |
для |
любой |
последовательности |
|||||||||||||
xn ,сходящейся к x0 ,последовательность |
f (xn ) сходится к a.При этом пишут |
lim f (x) a .Это |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
определение означает: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1.предел функции,если он существует,то он единственный |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2.значение функции вне интервала,содержащего точку |
x0 |
и |
в самой |
точке |
x0 ,не влияют |
на |
|||||||||||||||||||||
величину предела |
|
|
|
|
|
|
|
|
|
|
x0 |
, x0 ,содержащемся |
|
|
|||||||||||||
3.функция |
f(x) |
определена |
в |
некотором |
интервале |
в точке |
|||||||||||||||||||||
x0 ,кроме,быть может,самой |
x0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Определение 2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Число a наз пределом функции f(x) при x x0 |
,если |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
0 ( ) : x : x x |
0 |
f (x) a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема:Два оперделения эквивалентны |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1.Опр1 |
Опр2,т е выполнено опр1 xn : xn x0 |
:{ f (x)}сходится и |
lim f (xn ) a |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
Допустим,что lim не существует в смысле опр2.Это означает,что |
0 ,для которого нельзя |
||||||||||||||||||||||||||
подобрать |
,т |
е |
( ) : x |
: x x0 |
|
f (x ) a .Возьмем |
в качестве |
|
1 |
|
,тогда |
для |
|||||||||||||||
k |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
xk x |
1 |
f (xk ) a ,что |
противоречит |
опр1,следовательно,наше |
утверждение |
неверно и |
|||||||||||||||||||||
k |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
опр2 справедливо. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2.Опр2 |
Опр1,т |
е выполнено |
опр2 |
0 ( ) : x : x x0 |
f (x) a .Пусть |
xn - |
|||||||||||||||||||||
произвольная |
последовательность,сходящаяся |
к |
|
x0 ,тогда |
для |
данного |
выберем |
||||||||||||||||||||
N( ) : n N( ) xn x0 |
,тогда в силу опр2 |
f (xn ) a ,т е последовательность f (xn ) имеет |
|||||||||||||||||||||||||
пределом число a, а это означает,что lim f (x) a в смысле опр1. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание: lim |
f (x) b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 : x : x a |
f (x) b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
0 : x U a, f (x) U (b, ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
U ( , ) x : x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
U ( , ) {x : x } |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
U ( , ) {x : x } |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
19.Односторонние пределы.Примеры. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Пусть |
функция |
f(x) определена на |
(a, x0 ]([x0 ,b)) .В |
этом |
случае |
говорят |
об односторонних |
||||||||||||||||||||
пределах f(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 ( ) : x : x0 x x0 f (x) a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
( 0 : x : x0 x x0 f (x) a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1случай : |
|
lim |
f (x) A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x x0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 случай: |
|
lim |
f (x) A |
|
|
|
|
|
|
|
|
привести примеры! |
|
|
|
|
|
|
|
||||||||
|
|
x x0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В общем |
случае |
x (x0 ; x0 |
) ,в случае односторонних |
пределов |
этот интервал делится |
||||||||||||||||||||||
пополам. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10
