
matan1
.pdf
Т.о получим
f (x)
Pn (x) o((x
x |
|
) |
n |
) |
0 |
|
|||
|
|
|
|
, rn (x)
остаточный член формулы Тейлора.
Пусть функцияf(x) определена на интервале (a,b) и в каждой точке x0 принадлежащей интервалу (a,b) имеем производную до n порядка включительно, тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
f |
(k ) |
(x |
|
) |
|
f (x) Pn (x) o((x x0 ) |
n |
) , где |
Pn |
(x) ak |
(x x0 ) |
k |
, ak |
|
|
0 |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
k! |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Единственность многочлена Тейлора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пусть функция f (x) представлена в окрестности точки x0 многочлена вида |
||||||||||||||||||||||||||||||
n |
x x |
|
|
|
|
|
|
f |
(k ) |
(x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b |
|
, тог да b |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
k |
|
|
|
k |
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доказательство. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
f |
(k ) |
(x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
Если |
|
f (x) ak (x x0 )k , |
где ak |
|
k! |
0 |
|
|
еѐ многочлен Тейлора и есть у нас |
||||||||||||||||||||
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
другой многочлен bk (x x0 ) |
k |
|
|
ak (x x0 ) |
k |
|
bk |
(x x0 ) |
k |
надо показать, что |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
||
коэффициенты одинаковы
a |
0 |
a |
|
1 |
Пусть
a |
a |
2 |
1 |
|
на x
(x x |
|
) a |
|
(x x |
|
) |
2 |
..... a |
|
(x x |
|
) |
n |
b |
b (x x |
|
) b |
(x x |
|
) |
2 |
|
0 |
2 |
0 |
|
n |
0 |
|
0 |
0 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
|
|
|
|
x x0 a0 |
b0 |
сократим на |
x x0 |
|
|
|
|
|||||
(x x0 ) ... an (x x0 ) |
n 1 |
b1 |
..... bn (x x0 ) |
n 1 |
. пусть |
x x0 |
a1 |
|||||
|
|
|||||||||||
x |
0 |
и т.д. a |
n |
b |
многочлен Тейлора единственен. |
|
|
|||||
|
|
n |
|
|
|
|
|
|
|
|
||
Остаточный член формулы Тейлора в форме Лагранжа.
.....
b1
b |
(x x |
|
) |
n |
0 |
|
|||
n |
|
|
|
сократим
f (x) P (x) r |
(x) |
|
n |
n |
|
n
Pn (x) ak (x x0 )k
k 0
|
|
|
f |
(k ) |
(x |
|
) |
a |
|
|
|
0 |
|||
|
|
|
|
|
|||
k |
|
k! |
|
|
|||
|
|
|
|
|
|||
|
|
|
|
|
|
||
p |
n |
(x |
0 |
) |
|
|
|
ищем многочлен
|
f (x |
0 |
) |
|
|
|
Pn (x) ,который удовлетворяет следующим условиям:
можно записать в виде rn (x0 ) rn '(x0 ) ...rn |
(n) |
(x0 ) 0 |
|
P |
'(x |
0 |
) f |
'( |
||
n |
|
|
|
|
||
P |
n |
(x |
|
) a |
|
|
|
0 |
n |
||||
n |
|
|
|
|
||
рассмотрим
x0 ) |
|
|
|
эти условия |
f |
n |
(x |
|
) |
|
0 |
|||
|
|
|
|
функцию
(x) (x x0 )n 1 , (k ) (x0 ) 0k 0,1,2,...n
(n 1) (x0 ) (n 1)!
Рассмотрим отношение
r |
(x) |
|
r |
(x) r |
(x |
|
|
) |
|
r |
'(x |
) |
|
r |
'(x |
) r |
'(x |
|
|
) |
|
r |
''(x |
|
) |
|
r |
(n 1) |
(x |
|
) |
||||
|
0 |
(тКоши) |
|
0 |
|
2 |
.... |
|
|
n 1 |
|||||||||||||||||||||||||
n |
|
n |
n |
|
|
|
n |
1 |
|
n |
1 |
n |
|
|
|
n |
|
|
|
n |
|
|
|
||||||||||||
(x) |
(x) (x |
|
|
) |
'(x |
) |
'(x |
) '(x |
|
|
) |
''(x |
|
|
) |
|
|
(n 1)! |
|
||||||||||||||||
|
0 |
|
|
0 |
|
2 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
rn |
(x) |
(x)r (n 1) (x |
n |
1) |
|
|
|||
(n 1)! |
|
|||
|
|
|
||
(x) (x x |
0 |
)(n 1) |
|
|
|
|
|
|
|
|
|
|
|
где C (x, x |
0 |
) остаточный член в |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
r (n 1) (x |
|
1) f (n 1) |
(x |
|
1) r (x) |
(x x |
0 |
)n 1 f n 1 |
(c) |
|
|
|||||||
n |
n |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
n |
|
|
|
(n 1)! |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
форме Лангранжа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Формула Тейлора. |
f (x) Pn (x) |
(x x |
0 |
)n 1 f (n 1) (C) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
(n |
1)! |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
31

Следствие. Если |
|
f (x) Qn (x) произвольный многочлен степени n, то rn (x) |
|||||||||||||||||||||||
Q3 |
(x) x |
3 |
3x |
2 |
2x 1 |
разложим по степени (x-1). |
|||||||||||||||||||
|
|
||||||||||||||||||||||||
f (x) x |
3 |
|
3x |
2 |
2x 1 | |
|
|
3 |
|
|
|
|
|
|
|
||||||||||
|
|
x 1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f |
'(x) 3x |
2 |
6x |
2 | |
|
|
|
7 |
|
|
|
|
|
|
|
|
|||||||||
|
x |
1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f |
''(x) 6x 6 | |
x 1 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f |
'''(x) 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
3 |
3x |
2 |
2x 1 |
3 |
7 |
(x 1) |
12 |
(x 1) |
2 |
|
6 |
(x 1) |
3 |
|||||||||||
|
|
|
|
||||||||||||||||||||||
|
|
1! |
2! |
|
3! |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Проверка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x |
3 |
3x |
2 |
2x 1 (x 1) |
3 |
3x |
2 |
3x 1 3x |
2 |
2x 1 (x 1) |
3 |
6x |
2 |
5x 2 (x |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
12x 6 5x 2 (x 1) |
3 |
6(x 1) |
2 |
7x |
4 (x 1) |
3 |
6(x 1) |
2 |
7(x 1) 3 |
|
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
Справедлива теорема. Пусть функция y=f(x) имеет в окрестности точки |
x0 |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(x x |
0 |
)n 1 f (n 1) (C) |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||||
|
|
f (x) P (x) |
|
|
|
|
|
|
|
где С лежит между xиx |
|
, |
P (x) |
|
a |
|
(x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
k |
||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
(n 1)! |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|||||
|
|
|
f |
(k ) |
(x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0
1)3 6(x 1)2
x0 )k
Замечание№1 если |
x0 |
=0,то формула Тейлора называется формулой Маклорена. |
||||||||
Замечание№2 т.к f |
(k 1) |
(x) непреравна, то |
|
f |
(n 1) |
(c) |
|
M |
ограничена lim rn (x) |
|
|
|
|||||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
Формула Маклорена для функции e x
0
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
||
(ex )(k ) ex |
|
|
e x ak |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
||
a |
|
|
f (k ) (0) |
|
|
e0 |
|
|
|
1 |
|
||||
k |
|
|
|
|
|
|
|
||||||||
|
|
|
k! |
|
|
|
|
k! |
|
k! |
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x |
2 |
|
|
x |
3 |
|
|
|||
e |
x |
1 |
x |
|
... |
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
2! |
|
|
3! |
|
|
||||
|
|
|
|
|
|
|
n |
x |
k |
|
|
|
|||
Выражение |
|
|
|
e |
x |
||||||||||
|
|
|
|||||||||||||
k! |
|
||||||||||||||
|
|
|
|
|
|
k 0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
xk rn (x), an ?, rn ?
rn (x) 0(xn )
xn o(xn ) n!
ряд Маклорена.
|
|
n |
x |
k |
|
|
|
e |
x |
|
|
o(x |
n |
) |
|
|
|
||||||
|
|
|
|
|
|
||
|
|
k 0 |
k! |
|
|
|
|
|
|
|
|
|
|
|
|
Формула Маклорена для функции sin(x).
(sin x) |
(k ) |
sin(x |
k |
) |
|
||||
|
2 |
|||
|
|
|
|
K=0 |
Sinx |
| |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
K=1 |
Cosx |
| |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
K=2 |
-sinx |
| |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
K=3 |
-cosx |
| |
0 |
1 |
|
|
|
|
|
|
|
|
||
K=4 |
sinx |
|0 0 |
||
|
|
|
|
|
|
|
|
f |
(k ) |
(0) |
|
k |
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ak |
|
|
|
|
|
|
|
|
|
k-четное |
ak |
0 |
|
|
|
|
|||||||||||||||||
|
k! |
|
|
|
|
k! |
|
k! |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a |
|
|
|
|
|
1 |
|
|
|
|
|
a |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
4k 3 |
|
|
|
|
|
|
|
|
|
|
4k |
1 |
|
1)! |
|
|
|
|
|
|
|||||||||||||
|
|
(4k 3)! |
|
|
|
|
|
(4k |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
sin x |
1x |
|
0x2 |
|
1x3 |
|
|
0x4 |
|
|
1x5 |
... |
|
|
|
|
|||||||||||||||||
|
|
2! |
3! |
|
|
|
4! |
|
|
5! |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x |
3 |
|
x |
5 |
|
|
x |
7 |
|
|
|
|
|
x |
2n 1 |
|
n 1 |
|
2n 1 |
|
|||||||
sin x x |
|
|
|
|
|
|
.... |
|
|
|
|
( 1) |
o(x |
) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
3! |
|
5! |
|
|
7! |
|
|
|
(2n 1)! |
|
|
|
|
|
||||||||||||
Формула Маклорена для функции cos(x).
(cos x)(n) sin(x |
n |
) |
a |
|
|
f (k ) (0) |
|||
2 |
k |
k! |
|||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
N=0 |
Cosx |
|0 0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
32

N=1 |
-sinx |
| |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1x |
2 |
|
|
|
|
|
4 |
|
|
|
2n 2 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1x |
|
|
x |
|
|
|
|
|
|
|
|
|
||||||
N=2 |
-cosx |
|0 |
0 |
cos x 1 0x |
x |
3 |
|
.... |
( 1) |
n 1 |
o(x |
2n 2 |
) |
||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2! |
|
|
|
|
|
4! |
|
|
(2n 2)! |
|
|
|
|
|
|
|
|
|
||||
N=3 |
Sinx |
| |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=4 |
cosx |
| |
0 |
0 |
cos x 1 x2 |
x4 |
|
x6 |
.... |
x2n 2 |
|
( 1)n 1 |
o(x2n 2 ) |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
4! |
|
6! |
|
|
|
(2n 2)! |
|
|
|
|
|
|
|
||||||||||
Формула Маклорена для функции
(1 ) |
|
|
|
|
|
((1 x) |
|
) |
(k ) |
( 1)......( k 1)(1 ) |
k |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
f |
(k ) |
(0) ( 1)....( k 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
n |
|
( 1)......( k 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
(1 x) |
|
|
|
x |
k |
0(x |
n |
) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
1 x |
x |
2 |
x |
3 |
|
x |
4 |
x |
5 |
|
... ( 1) |
n |
x |
n |
o(x |
n 1 |
) |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
y=ln(1+x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
[ln(1 x)] |
(n) |
|
|
|
|
|
|
|
( 1) |
n 1 |
(n 1)' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x |
1) |
|
|
|
|
|
|
|
|
||||||||||||||
( f |
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
(k ) |
|
) ( 1) |
k |
1 |
(k 1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0 |
|
| |
|
|
|
( 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
f |
k |
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
, k 1,2,..n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
k |
|
|
k! |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
x |
3 |
|
x |
4 |
|
|
x |
5 |
|
|
x |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
|
|
|
|
|||||||
ln(1 x) x |
|
|
|
|
|
|
|
|
|
|
|
|
|
.... ( 1) |
n 1 |
|
o(x |
n |
) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||||||||
f (0) ln(1 0) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Пример. Написать формулу Маклорена для функции |
y cos |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
y cos t 1 |
t 2 |
|
t 4 |
|
|
t 6 |
.... |
t 2n |
|
|
|
( 1)n 1 |
r |
(t) |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
|
|
4! |
|
|
6! |
|
|
|
|
|
(2n)! |
|
|
|
|
|
|
n |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x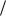 3
3
. Решение: обозначим
t=x/3 , |
|
x |
2 |
|
x |
4 |
|
x |
6 |
|
x |
2n |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
3 |
|
|
3 |
|
|
3 |
|
.... |
3 |
|
( 1) |
n 1 |
r |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2! |
|
4! |
|
6! |
|
(2n)! |
|
|
n |
3 |
|
|||||||||
Пример
y cos(2x 3)
формула Маклорена по степеням x
|
|
|
|
|
|
|
|
|
(2x) |
2 |
|
(2x) |
4 |
|
(2x) |
6 |
cos(2x 3) cos 2x cos 3 sin 2x sin 3 cos 3(1 |
|
|
|
|
...) sin 3* |
|||||||||||
2! |
|
4! |
|
6! |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(2x) |
3 |
|
(2x) |
5 |
(2x) |
7 |
|
|
|
|
|
|
|
|
|
* (2x |
|
|
|
...) |
|
|
|
|
|
|
|
|
||||
3! |
|
|
5! |
7! |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Исследование поведения функции. Признак монотонности функции. |
|||||||||||||||
Теорема. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть функция |
f (x) |
дифференцируема на интервале (a,b). Тогда если f '(x) 0 то |
||||||||||||||
функция возрастает, если P'(x) 0 , то функция убывает. Доказательство.
33

Пусть |
a x1 x2 |
b |
по формуле Лангранжа, имеем f (x2 ) f (x1 ) f '( )(x2 x1 ) |
|||
x1 x2 , т.к x2 |
x1 |
0 , то |
|
|
||
1) |
если |
f '( ) 0, тоf (x2 ) f (x1 ) 0 |
|
|
||
2) |
если |
f '( ) 0, тоf (x2 ) f (x1 ) 0 т.е в1) f(x) возрастает, в 2) f(x) убывает; |
||||
f(x) возрастает , если x1 x2 , f (x1 ) f (x2 ), f (x) убывает, если для x1 x2 , |
f (x1 ) |
|||||
данные условие достаточное условие, но не является необходимым. y x |
3 |
всюду |
||||
|
||||||
возрастает, но y’(0)=0.
, где
f (x |
2 |
) |
|
|
Наибольшее и наименьшее значение функции.
Было
Точка x0 называется максимумом(минимумом) функции f(x), если
U (x |
) : x U (x |
) f (x |
) f (x)( f (x |
) f (x)) |
|||
|
0 |
|
|
0 |
0 |
0 |
|
U (x |
) U (x |
) \ x |
0 |
|
|
|
|
0 |
|
0 |
|
|
|
|
|
Точка x0 называется максимумом(минимумом) функции f(x),
если |
: x : |
|
x |
|
|
выполняется |
|
|
|||||||
|
|
|
|
||||||||||||
неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (x |
0 |
x) f (x |
0 |
)( f (x |
0 |
x) f (x |
0 |
)) |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Обозначим f |
|
f (x0 x) f (x0 ) |
|
|
|
|
|||||||||
Если точка x0 |
точка максимума, то |
|
f |
<0. |
|||||||||||
Если точка х0 |
точка минимума, то |
f >0. |
|||||||||||||
При переходе через точки экстремума f не меняет знак.
Исследование поведения функции.
Теорема 1. Необходимое условие экстремума. Пусть точка х0 является точка экстремума для функции f(x). Тогда, если существует f’(x0), то f’(x0)=0, либо f’(x0) не существует.
В точке х1 – min; в точке х2 – max.
Теорема 2. Достаточное условие строгого extr в терминах первой производной. Пусть f(x) дифференцируема в некой окрестности точки х0, и в точке х0 f(x) непрерывна. Если f’(x) при переходе через точку х0 меняет знак, то точка х0 является точкой строгого
экстремума, при этом 1)если при x0 x x0 , f '(x) 0 , а при x0 |
x x0 |
, f '(x) 0 |
то в точке х0 – минимум. 2)если при x0 x x0 , f '(x) 0 , а при |
|
|
x0 x x0 , f '(x) 0 то в точке х0 максимум. |
|
|
Доказательство. Докажем 1) f (x) f '( )( x) .Теорема Лангранжа |
|
|
f (x) f (x0 ) f '( )(x x0 ) . а) Если х-х0>0 и f '( ) 0, тоf (x) f (x0 ) f |
0 . б) если х- |
|
34

х0<0 и f '( ) 0, тоf (x) f (x0 ) f 0 , т.е при переходе через точку х0 |
f |
свой знак: f >0, т.е точка х0-точка минимума. |
|
2)Доказательство аналогично.
Достаточное условие строгого экстремума в терминах старшей производной. Пусть в точке х0 у функции f(x) существует n производных, причѐм
не меняет
f '(x |
|
) f ''(x |
|
) ... f |
(n 1) |
(x |
|
) 0, |
f |
(n) |
(x |
|
) |
0 |
0 |
|
0 |
|
0 |
||||||||
|
|
|
|
|
|
|
|
|
|
экстремум, и если f (n) (x0 ) 0 min . f (n) (x0 )
0.
Тогда, если n=2k, то в точке х0
0 max . Если n=2k+1 в точке х0 нет
экстремума и точка х0 точка возрастания. Если
f
(n)
(x |
0 |
) 0 |
|
|
и точка убывания,
 если
если
f
(n)
(x |
0 |
) |
|
|
0
.
Следствие. Если в точке х0 у функции f(x) существует f |
(k ) |
(x0 ) |
||
|
||||
точке х0 минимум, f |
(k ) |
(x0 ) <0,то в точке х0 максимум (k=1). |
||
|
||||
Доказательство. Разложим функцию f(x) в ряд Тейлора.
, то, если
f
(k ) |
|
) |
(x |
0 |
|
|
|
>0, то в
|
|
|
f (n) (x0 ) |
|
|
|
|
|
|
|
|
f f (n) (x |
0 ) (x)n |
o(x)n знак |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
f (x) f (x |
0 |
) |
(x x |
0 |
)n o(x x |
0 |
)n или |
|||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f определяется первым слагаемым, если n – четное, то знак |
f зависит от знака |
|||||||||||||||||||||||||||
f |
(n) |
(x0 )((x) |
(n) |
0) |
. По этому, если |
f |
(n) |
(x0 ) 0 |
то f >0 – минимум. |
f |
(n) |
(x0 ) 0 то |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
f <0 – максимум. Если n – нечетное, то знак f |
зависит от |
x и f |
(n) |
(x0 ) , т.е. при |
||||||||||||||||||||||||
|
||||||||||||||||||||||||||||
переходе через точку х0 знак |
f меняется, следовательно в точке х0 экстремума нет. |
|||||||||||||||||||||||||||
Следствие. |
|
f |
|
f ''(x |
0 |
) |
(x) |
2 |
o(x) |
2 |
. f’’(x0)>0, |
f >0 – минимум; f’’(x0)<0, f <0 – |
||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
2! |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
максимум.
Выпуклости функции. Точка перегиба.
Опр. Функция f(x) на интервале (a,b) называется выпуклой вверх (выпуклой вниз), если
x |
, x |
2 |
(a,b) |
1 |
|
|
x |
x |
2 |
|
|
|
f |
1 |
|
|
||
|
|
|
|||
|
|
2 |
|
|
|
f (x1 ) f (x2 )
2
(
x |
x |
|
|
|
|
f |
1 |
|
2 |
|
|
|
|
|
|
||
|
|
2 |
|
|
|
f (x |
) |
1 |
|
|
2 |
f
(x |
2 |
) |
|
|
)
Геометрически это означает что кривая y=f(x) лежит выше(ниже) прямой.
Достаточное условие строго выпуклости.
Теорема. Если на интервале (a,b) f’’(x)>0, то f(x) выпукло вниз, если f’’(x)<0, то f(x) выпукло вверх.
Доказательство 
35

Рассмотрим разность
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x |
2 |
) |
|
|
|
f (x |
|
|
|
|
|
|
x |
x |
2 |
) |
|
|
|
|
||||||
|
|
x |
|
|
|
|
|
|
|
) |
|
|
|
|
|
2 f ( |
|
1 |
|
|
f (x |
) |
|
) |
|
f ( |
1 |
|
|
|
f (x |
) |
||||||||||||||||
x |
|
|
|
|
f (x |
|
f (x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
2 |
|
|
|
2 |
x |
|
|
|
2 |
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|||||||||||||||
f |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
f (x |
|
) |
|
f ( |
x |
x |
|
) |
|
|
|
|
|
|
|
|
|
|
f |
'( )( |
x |
x |
|
x ) |
|
|
f |
'()(x |
|
|
|
x |
x |
|
) |
|
||||||||||||
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
1 |
|
|
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
Т.Ланг ранжа |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f '( ) |
(x |
|
|
x |
) |
|
f |
'() |
(x |
|
x |
) |
(x |
|
x |
) |
( f ' |
( ) |
f '()) |
(x |
|
x |
) |
f |
'' |
( )( ), г де ( ,) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
|
|
2 |
|
|
1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 |
|
|
|
2 |
|
|
1 |
|
|
|
|
4 |
|
|
2 |
|
1 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
х2-х1>0
0
а)Если
б) Если
x |
x |
|
|
|
|
|
f ''( ) 0, тоf |
1 |
|
2 |
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
x |
x |
|
|
|
||
f ''( ) 0, тоf |
1 |
|
|
2 |
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
f (x |
) |
f (x |
2 |
) |
||
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
f (x |
) |
f (x |
2 |
) |
||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
выпукла вниз.
выпукла вверх.
Опр. Точка х0 для функции f(x) называется точкой перегиба, если она является концом интервала выпуклота вверх(вниз) и началом интервала выпуклота вниз(вверх)
Необходимое условие точек перегиба.
Если функция дважды непрерывна, дифференцируема в точке х0 и если точка х0 является точкой перегиба, то f’’(x0) = 0
Доказательство. Если бы f’’(x0)>0 то в некоторой окрестности точке х0 f(x) была выпукла вниз. Если бы f’’(x0)<0 то в некоторой окрестности точке х0 f(x) была выпукла вверх. Но это противоречит определению точке перегиба: точка перегиба не принадлежит ни какому интервалу выпуклости.
Достаточное условие точки перегиба.
Если функция f(x) дважды дифференцируема в некоторой окрестности точке х0 кроме, быть может, самой точки х0, но f(x) непрерывна в точке х0 и ее производная меняет знак при переходе через точку х0, то в точке х0 – точка перегиба.
Доказательство.
1) : x (x0 , x0 ) f ''(x) 0x (x0 , x0 ) f ''(x) 0
либо
2) : x (x0 , x0 ) f ''(x) 0
x (x0 , x0 ) f ''(x) 0
Т.е. в случае (1) точка х0 является концом интервала выпуклости вверх и началом интервала выпуклости вниз, следовательно точка х0 точка перегиба. В случае (2) точка х0 является концом интервала выпуклости вниз и началом интервала выпуклости вверх, следовательно х0 точка перегиба.
Замечание. Заметим, что если функция y=f(x) выпукла вниз, то ее график лежит выше касательной, если функция y=f(x) выпукла вверх, то ее график лежит ниже касательной.
Теорема. Пусть функция f(x) обладает следующим условием |
|
|
|
|
||||||||
f ''(x |
0 |
) .... f (n) (x |
0 |
) 0, f (n 1) (x |
0 |
) |
непрерывна в точке x0 и |
f (n 1) |
(x |
0 |
) 0 |
.n-четное y= f(x) |
|
|
|
|
|
|
|
|
|
||||
36

выпукла вверх, если
точка перегиба. Доказательство.
f |
(n 1) |
|
0
и выпукла вниз, если
f |
(n 1) |
|
0
, n+1-нечетное- точка x0-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
(n 1) |
(x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
f (x |
|
) f '(x |
|
)(x x |
|
) |
|
0 |
(x x |
|
) |
n 1 |
o((x x |
|
) |
n 1 |
) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
0 |
0 |
0 |
(n 1)! |
|
0 |
|
0 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
f |
(n 1) |
(x |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f (x) y |
|
|
|
0 |
(x x |
|
) |
n 1 |
0((x x |
|
) |
(n 1) |
) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
кас |
|
(n 1)! |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n+1- четное следовательно положение функции у нас зависит только от производной
f (n 1) (x0 ) . N-нечетное y(x)>y(кас), если f (n 1) 0 . y(x)<y(кас), если f (n 1) |
0 , точка X0- |
|
точка перегиба. |
|
|
Теорема Ферма (необходимое условие extr). |
|
|
Пусть f (x) определена на интервале (a,b) и точка (a,b).если в точке |
функция f(x) |
|
достигает max или min значения и в точке существует производная, то f’( )=0. |
||
Доказательство. |
|
|
Пусть для определенности в точке |
f (x) принимает max значение, т.е |
|
f ( )
тогда
ff
(x) x
|
'( )uf |
|
' |
|
|
(a,b) . В точке существует производная |
f '( ) lim |
f (x ) |
|
x |
|||
|
x 0 |
||
( ) (правая и левая производная).Распишем отношение |
|||
f ( )
,
|
|
x 0, |
f (x ) f ( ) |
0 |
|
|
f (x ) f ( ) |
x |
|
|
|||
|
переходя в этих интервалах к пределу, |
|||||
|
|
|
||||
x |
|
|
f (x ) f ( ) |
|||
|
x 0, |
0 |
|
|
||
|
|
x |
|
|
||
|
|
|
|
|
|
|
получим |
f '( ) 0 |
|
|
|
|
|
f '( ) |
0, f '( ) f '( ) f '( ) 0 |
|
|
|||
|
|
|
||||
Замечание. |
|
|
|
|
|
|
Теорема носит локальный характер, т.е. точка |
|
является локальным экстремумом. |
||||
Геометрический смысл теоремы.
В предположение теоремы всегда существует точка, в которой касательная к графику функции параллельная OX.
Теорема Ролля.
Пусть функция y= f (x) :
1)непрерывна на отрезке [a,b];
2)дифференцируема (a,b);
3)f(a)=f(b), тогда : f '( ) 0.
Доказательство.
Функция f(x), непрерывна на [a,b] достигает на нем max M и min m значения, т.е m f (x) M . Возможны два случая.
1)m M f (x) c const и f '(x) 0
2)m M (m M ) ,тогда либо максимальное значение f(x) либо минимальное значения f(x) достигается внутри интервала (a,b) (не на конце отрезка [a,b]).(f(a)=f(b)).
37

min (a,b) : f ( ) M , тогда f (x) достигает максимального или минимального значения во внутренней точке интервала (a,b) и по теореме Ферма f '( ) 0 //
x,0 x 1 |
|
f (x) |
|
0, x 1 |
|
|
|
f (x) | x |
| |
x [ 1,1] |
|
f (x) x [0,1]
Все условия теоремы Роля существенные.Если выполняется, только 2 из 3(см. картинку), то не существует точка причем f '( ) 0 (касательная параллельная оси ОХ). Интегрирование подстановкой(подведение под знак дифференцирования).
|
f (x)dx |
|
f (x(t))x'(t)dt |
( x'(t)dt dx ) в две стороны. |
|
|
В некоторых случаях неудобно t выражать через x, и поэтому делаем замену
x (t)
|
|
|
dx |
|
|
|
|
dx |
|
|
t x |
|
|
|
||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
|
|||||||||||
cos x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
sin(x |
) |
dt dx |
|
|
|
|||||||||
|
|
|
|
|
|
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11. |
|
a |
2 |
x |
2 |
dx |
x a sin t |
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
dx |
a cos tdt |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a |
2 |
cos |
2 |
tdt a |
2 |
|
1 cos 2t |
dt |
||||||||||
|
|
|
||||||||||||||||
|
|
|
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dt |
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
a |
2 |
a |
2 |
sin |
2 |
ta cos tdt a |
1 sin |
2 |
ta cos tdt |
|
|
|||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
x |
sin t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
2 |
|
|
|
sin 2t |
|
|
|
x |
|
|
|
|
|
|
|
||
|
|
|
C t arcsin |
|
|
|
|
|
|
|
||||||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
2 |
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
a |
2 |
x |
2 |
|
|
|
|
|
|
|
|
|
sin 2t 2 sin t cos t 2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a |
2 |
|
x |
|
x |
a |
2 |
x |
2 |
|
a |
2 |
|
x |
|
x |
|
|
|
|
|
|
(arcsin |
(2 |
|
|
) / 2) C |
|
arcsin |
|
a |
2 |
x |
2 |
C |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
a |
a |
|
|
a |
|
2 |
a |
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Если интеграл содержит Если интеграл содержит
тождестве 1 tg |
2 |
t |
1 |
|
||||
|
|
|||||||
|
cos |
2 |
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
1 tg |
2 |
t |
и т.д. |
|
||
|
|
|
||||||
|
2 |
|
|
|||||
cos |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

 a2
a2
x |
2 |
|
|
,1 |
|
t |
|
x2 , то либо x=asint,
a2 , то замена такая
ctg |
2 |
t |
1 |
ch |
2 |
t |
|
|
|
||||||
|
|
2 |
|
||||
|
|
|
sin |
t |
|
|
|
|
|
|
|
|
|
||
либо x=acost (оси на cos |
2 |
t |
sin |
2 |
t 1 ). |
||||
|
|
||||||||
x |
a |
, x |
a |
, x arht |
основано на |
||||
|
|
||||||||
|
cos t |
sin t |
|
|
|
|
|
|
|
2 |
t 1 |
(каждое надо записать в виде) |
|||||||
sh |
|||||||||
Если интеграл содержит 
 x2 a2 , то замена либо x=a*tgt, x=a*ctgt, x=a*sht. 12
x2 a2 , то замена либо x=a*tgt, x=a*ctgt, x=a*sht. 12
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x t |
|
|
|
|
|
|
|
t 2 |
|
|
|
|
|
|
|
t 2 |
|||
|
|
|
x 1 |
|
|
|
|
|
2 |
|
|
|
t 1 |
|
|
t |
|
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
dx x t |
|
|
|
|
|
|
2tdt 2 |
|
|
|
dt 2 |
|
t 2 |
|
|
dt 2( |
|
2t 2 ln(t 1)) C |
||||
|
|
|
|
|
|
|
|
t 1 |
t |
|
|
|
|
||||||||||||||||
|
|
x 1 |
|
|
dx 2tdt |
|
1 |
|
|
|
t 1 |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2( |
2 |
|
x 2 ln |
x 1 C). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
38

13. |
|
|
|
2 |
dx |
2 |
|
(x |
a |
||||
|
|
|
|
|||
|
|
|
|
|
||
1 |
|
(1 cos |
||||
2a |
3 |
|||||
|
|
|
|
|
|
|
|
|
x atgt |
|
|
|
|
|
|
|
|
adt |
|
|
|
|
|
|
1 |
|
dt |
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
2 |
tdt |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
) |
2 |
dx a |
|
|
cos |
2 |
t(a |
2 |
tg |
2 |
t a |
2 |
) |
2 |
a |
3 |
cos |
2 |
a |
3 |
|
|
|
|
||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
cos |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
4 |
t |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2t)dt |
1 |
|
(t |
|
sin 2t |
) C |
1 |
|
(t |
|
|
2sin t cos t |
|
|
) C |
1 |
|
(t |
tgt |
) C |
||||||||||||||||||
|
3 |
|
|
|
|
3 |
|
|
|
2 |
|
|
|
|
2 |
|
3 |
2 |
|
|||||||||||||||||||
|
|
|
2a |
|
|
|
2 |
|
|
|
|
|
2a |
|
|
2(sin |
t |
cos |
t) |
|
|
|
2a |
tg |
t 1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
(arctg |
x |
|
|
a |
) C |
|
2a |
3 |
a |
x |
|
2 |
|||
|
|
|
1 |
|||||
|
|
|
|
|
|
|
||
|
|
|
|
( |
a |
) |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2a |
3 |
|
(arctg
x a
|
|
ax |
|
) C |
|
a |
2 |
x |
2 |
||
|
|||||
|
|
|
.
Пусть
Интегрирование по частям.
и -2 заданные функции, которые являются дифференцируемыми, тогда
d( ) d d .
|
|
|
|
|
|
|
|
|
|
d ( ) |
|
d |
d |
или |
|
d |
d |
Применяется для вычисления интегралов.
1.
|
|
|
|
ax |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
P (x) , : dx d |
|
P (x) |
sin ax |
|
dx |
||||||
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos ax |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arcsin x |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arccos x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: , dx d |
2. |
Pn (x) arctgx |
dx |
|||||||
|
|
|
|
|
arcctgx |
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
|
|
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или
d
|
|
|
d |
.
Замечание. функции{} у которых есть алгебраическая производная.
3. |
|
|
|
arcsin x |
|
|||
P (x) |
|
arctgx |
|
dx |
|
|
|
||||
n |
|
|
|||
|
|
|
|
|
|
|
ln x |
|
|
||
|
|
|
|
||
(arcsin x arccos x |
|
, arctg arcctg |
|
) |
|
2 |
2 |
||||
: |
|
|
|||
|
|
|
|
||
P (x) dx d |
|
|
|
|
|
n |
|
|
|
|
4. |
|
|
x |
cos bx |
формула интегрирования по частям применяется два раза либо |
||||
|
|
dx |
|||||||
|
|
||||||||
|
|
|
sin bx |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Оба раза, либо |
-тригонометрическая функция оба раза.Получаем???? уравнение, |
||||||||
которое далее решаем. |
|
|
|||||||
14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x sin xdx |
sin xdx d |
x( cos x c) |
(c cos x)dx x cos x xc cx |
||||||
d dx |
|
x cos x sin x C |
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
sin dx cos x c |
|
|
||
замечание. произвольную постоянную писать не надо.
-??????
sin x C
39

15. |
|
|
arctgx |
|
|
|
|
|
|
|
|
|
|
|
dx d |
|
|
|
xdx |
|
|
1 |
|
|
|
|
arctgxdx |
dx |
|
xarctgx |
|
|
xarctgx |
ln(1 x |
2 |
) C |
||
|
|
|
|
|
|||||||
|
|
x |
2 |
|
|
||||||
d |
x |
2 |
|
1 |
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
16. |
|
|
|
|
|
|
ln |
2 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
x |
2 |
dx |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
2 ln xdx |
|
x |
3 |
|
|
x |
x |
3 |
2 ln x |
|
x |
3 |
|
|
|
2 |
x |
|
|
x |
2 |
ln |
2 |
xdx d |
|
|
ln |
2 |
|
dx |
|
ln |
2 |
x |
2 |
ln xdx |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
x |
3 |
|
3 |
x |
3 |
|
3 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ln x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x |
2 |
dx |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
d |
|
|
x |
3 |
|
|
|
|
|
|
x |
3 |
|
|
|
|
x |
3 |
dx |
|
|
x |
3 |
|
|
|
2x |
3 |
|
|
2x |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
d |
|
|
|
ln |
2 |
|
x 2 / 3( |
ln x |
|
) |
|
|
ln |
2 |
x |
ln x |
|
|
C |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
x |
|
|
|
3 |
|
|
|
9 |
|
|
|
9 * 3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos bx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax |
dx d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax |
cos bx |
|
|
|
ax |
|
|
|
|
|
|
e |
ax |
cos bx |
|
b |
e |
|
|
|
|
|
|||||||||||||
I |
ax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b sin bx)dx |
|
|
ax |
sin bxdx |
|||||||||||||||||||||||||||||
cos bxdx d b sin bxdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin bx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
e |
ax |
dx |
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
e |
ax |
cos bx |
|
b |
|
e |
ax |
|
|
|
|
|
e |
ax |
|
|
|
|
|
|
e |
ax |
cos bx |
|
b |
|
|
|
|
b |
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
ax |
|
|
|
|
|
|
|
|
|
|
|
( |
|
sin bx |
|
|
b cos bxdx) |
|
|
e |
ax |
sin bx |
|
I |
|||||||||||||||||||||||||
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
a |
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
|
|
|
a |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
d b cos bxdx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
b |
2 |
|
|
e |
ax |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I (1 |
|
) |
(a cos bx b sin bx). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
a |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Интегрирование рациональных дробей.
P (x) a |
0 |
|
n |
|
дробь. Если правильной.
a1 x ...... an x |
n |
|
0 ). R(x) |
P (x) |
|
||
-многочлен степени n ( an |
n |
|
-рациональная |
||||
|
Q |
|
(x) |
||||
|
|
|
|
m |
|
||
|
|
|
|
|
|
|
|
n>=m, то дробь называется неправильной. Если n<m, то дробь называется Если R(x)-неправильная рациональная дробь, то разделим уголком
числитель на знаменатель, обозначим q(x)-частное,r(x)-остаток.
R(x) q(x) |
r(x) |
||
Q |
|
(x) |
|
|
m |
||
|
|
|
|
-
правильная дробь. q(x)-многочлен - легко интегрируется, надо научится интегрировать правильную рациональную дробь.
Q (x) b |
b x ...... b xm |
b 0 |
*********************** |
||
m |
0 |
1 |
m |
m |
|
40
