1.2 Движение электронов в атоме

Каждый атом или молекула может находиться в том или другом энергетическом состоянии. Иначе говоря, их внутренняя энергия квантована.

Взаимодействие частиц в квантовой механике характеризуют потенциальной энергией, формула которой заимствуется из классической механики. Например, потенциальная энергия заряженной частицы (например, электрона с зарядом минус q) в электрическом поле другой заряженной частицы (например, ядра атома водорода c зарядом плюс q) выражается формулой

,

(1.12)

Эту формулу и переносят в квантовую механику как формулу, характеризующую электрическое взаимодействие двух заряженных частиц.

В этом случае уравнение Шрёдингера примет вид:

,

(1.13)

Уравнение в частных производных (1.13) имеет множество решений. В каждой конкретной задаче из этого множества следует выбрать одно решение, отвечающее условиям задачи.

Геометрический образ, соответствующий и представляющий область наиболее вероятного пребывания электрона в атоме, называют атомной орбиталью данного электронного состояния. Кстати, из-за неопределенности координат нельзя говорить и о траектории электрона, в частности об орбитах электронов в атомах.

Для описания электронной системы, будь то атом, молекула или кристалл необходимо знать все её возможные квантовые состояния, характеризуемые энергетическим спектром системы (кристалла, атома). Если электронная система находится в равновесии и не подвергается никаким внешним воздействием, то находящиеся в ней электроны должны занимать состояния с минимальной энергией.

Решения уравнения Шрёдингера существуют только для волновых функций, характеризуемых набором целых чисел (которые называют квантовыми): n, l, m и соответствующих им дискретных значений энергий.

Главное квантовое число n может принимать любые целые положительные значения от 1 до ∞. Оно определяет величину энергии и влияет на размеры атомной орбитали – пространства, в котором велика вероятность нахождения электрона. С увеличением n расстояние между энергетическими уровнями и энергия связи электронов с ядрами уменьшается, значение энергетического зазора между уровнями падает.

	(1.14)
	(1.15)

Здесь Z – порядковый номер элемента в таблице Д.И. Менделеева.

Орбитальное квантовое число l определяет форму орбитали. Значение орбитального числа l=(n-1)= 0, 1, 2, 3, … , (n-1). Также вводят буквенные обозначения: 0-s, 1-p, 2-d, 3-f.

Магнитное квантовое число характеризует величину магнитного поля, создаваемого при вращении электрона вокруг ядра. Поэтому значение магнитного квантового числа m связано со значением орбитального квантового числа и изменяется от –l до + l, а всего число может принимать (2l + 1) значение, включая нулевое. Например, для l = 2: m = -2, -1, 0, 1, 2.

Сколько электронов может находиться на одной орбите? Вольфганг Паули в 1925 г. сформулировал принцип запрета: на любой атомной орбите может находиться не более двух электронов. Если бы этого не наблюдалось, все электроны в сложных атомах перешли бы на самый нижний энергетический уровень.

В том же 1925 г. голландец Ральф Кронинг и независимо Джордж Уленбек и Самюэль Гаудсмит предположили, что электрон вращается вокруг собственной оси. Внутренний момент импульса, связанный с этим вращением, назвали спином (от англ. spin – вращение), а момент, связанный с вращением вокруг ядра – орбитальным моментом. Но какая ось у электрона – материальной точки? Там не менее, существенно, что электрон помимо координат и импульса характеризуется вектором спина, спин, подобно заряду, - внутренняя характеристика электрона, в классической теории аналогичного понятия быть не может. Спиновое число s =+½. Спин – это одно из проявлений принципа тождественности частиц, который применительно к электронам звучит так: все электроны Вселенной неразличимы. В квантовой теории сама постановка вопроса: что в этой точке находится электрон №8, не имеет смысла. Электроны, как и фотоны, можно изучать лишь в совокупности.

В 1940 г. тот же Паули выдвинул теорему, согласно которой для частиц с полуцелым спином (фермионов) выполняется принцип запрета (на одной орбитали находится не более 2s+1 частиц).

У фотона, глюона (осуществляет обмен между кварками) s =1 – целое число, в одном состоянии может находиться любое число частиц.

Свое название – фермионы, частицы с полуцелым спином (электроны, дырки) получили по имени итальянского физика Энрико Ферми. Частицы с целым спином (включая нуль) – бозоны, по имени индийского ученого Шатьендраната Бозе.

Схема заполнения атомных оболочек отражена в периодической таблице элементов Менделеева: порядковый номер элемента Z соответствует числу электронов атома, номер периода, показывает значение главного квантового числа внешней оболочки атома (n = 1, 2, 3, 4, 5, 6, 7). Группа, в которой находится элемент, указывает число электронов, находящихся на внешней оболочке, для которой главное квантовое число соответствует номеру периода.

Электрону, находящемуся в атоме, можно сообщить энергию, достаточную для того чтобы он не только перешел на более высокий возбужденный уровень, характеризующийся следующим главным квантовым числом n, но и стал свободным. Атом при этом превращается в положительно заряженный ион. Соответствующую энергию называют энергией ионизации атома.
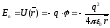