
- •1 Движение электрона в кристалле. Уравнение Шрёдингера, волновая функция
- •1.2 Движение электронов в атоме
- •1.3 Зонная теория твердого тела
- •Глава 2. Электропроводность полупроводников
- •2.1 Собственные и легированные полупроводники. Уравнение электронейтральности
- •2.2 Статистика электронов и дырок
- •2.2.1 Заполнение электронами зон вырожденного полупроводника
- •2.2.1 Заполнение электронами и дырками зон невырожденного полупроводника
- •2.2 Положение уровня Ферми и расчет концентрации носителей
- •2.2.1 Донорный полупроводник
- •2.3 Электропроводность полупроводников
- •2.3.1 Электронная проводимость
- •2.3.2 Дырочная проводимость
- •2.3.3 Собственная проводимость
- •Глава 3. Неравновесные электронные процессы
- •3.4 Диффузионный и дрейфовый токи
- •3.2. Неравновесные носители в электрическом поле
- •3.2.1. Уравнение непрерывности тока
- •5 Контакт электронного и дырочного полупроводников
- •5.1 Возникновение потенциального барьера. Контактная разность потенциалов.
- •5.2 Вольтамперная характеристика p-n-перехода
- •5.3 Температурные зависимости вах pn-перехода
- •5.3 Влияние генерационно-рекомбинационных процессов на вах pn-перехода.
- •5.4 Барьерная емкость pn-перехода
- •5.5 Диффузионная емкость pn-перехода
- •5.6 Пробой pn-перехода
- •5.6.1 Лавинный пробой pn-перехода
- •5.6.2 Туннельный (полевой, зинеровский) пробой pn-перехода
- •5.6.3 Тепловой пробой pn-перехода
- •5.7 Влияние сопротивления базы на вах pn-перехода. Полупроводниковый диод
- •5.8 Выпрямление на полупроводниковом диоде
- •5.8.2 Переходные процессы в полупроводниковых диодах
- •5.9 Полупроводниковые диоды
- •5.9.1 Выпрямительные диоды
- •5.9.2 Стабилитроны
- •5.9.3 Туннельные диоды
- •6 Биполярные транзисторы
- •6.1 Включение транзистора по схеме с общей базой
- •6.1.1 Статические вольт-амперные характеристики транзистора, включенного по схеме с общей базой
- •6.1.2 Усиление транзистора, включенного по схеме с общей базой
- •6.2 Включение транзистора по схеме с общим эмиттером
- •6.2.1 Статические вольт-амперные характеристики транзистора, включенные по схеме с общим эмиттером
- •6.3 Включение транзистора по схеме с общим коллектором
- •6.4. Дифференциальные параметры биполярного транзистора
- •6.4.1 Температурная зависимость параметров биполярных транзисторов
- •6.5 Работа транзистора в импульсном режиме
- •7 Тиристоры
- •7.1 Вольт-амперная характеристика тиристора
- •7.2 Типы тиристоров
- •8 Униполярные транзисторы
- •8.1 Полевой транзистор с управляющим pn- переходом (птуп)
- •8.1.1 Вольт-амперные характеристики птуп
- •Мдп–структура
- •1. Идеальная мдп-структура
- •2 Вольт-амперные характеристики мдп-транзистора
- •8.2.2 Схемы включения мдп-транзистора
- •4.2. Барьер на границе металла с полупроводником (барьер Шоттки)
- •4.2.1 Выпрямление тока на контакте металла с полупроводником
- •Фотоэлектрические полупроводниковые приборы
- •7.2. Полупроводниковые источники оптического излучения
- •10 Классификация интегральных микросхем
- •10.2 Условные обозначения микросхем
- •10.3 Элементы микросхем
- •10.4 Технология изготовления микросхем
- •10.4.1 Корпуса микросхем
1 Движение электрона в кристалле. Уравнение Шрёдингера, волновая функция
Все окружающие нас тела состоят из элементарных частиц (атомов) или из групп определенным образом объединенных атомов (молекул). Любая молекула состоит из совокупности электронов и атомных ядер, движение и взаимное расположение которых определяют значение внутренней энергии молекулы.
В
1924 г. французский физик Луи де Бройль
предположил, что любая частица, в том
числе и электрон, обладает волновыми
свойствами с длиной волны
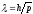 ,
гдеh
= 6,62·10-34
Дж·с=4,5·10-15
эВ·с – постоянная Планка;
,
гдеh
= 6,62·10-34
Дж·с=4,5·10-15
эВ·с – постоянная Планка;
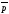 –
импульс электрона. Такую волну стали
называтьволной
де Бройля.
–
импульс электрона. Такую волну стали
называтьволной
де Бройля.
Можно
ввести понятие волнового
числа, то
есть числа волн, укладывающихся на 2 см:
см: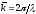 =
=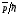 ,
где
,
где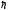 =
= = 1,054 10-34 Дж
с – приведенная постоянная Планка или
постоянная Дирака.
= 1,054 10-34 Дж
с – приведенная постоянная Планка или
постоянная Дирака.
Тогда
можно связать импульс с волновым
вектором:
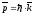 ,
что и сделал де Бройль. В этом случае
,
что и сделал де Бройль. В этом случае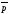 называют квазиимпульсом электрона.
называют квазиимпульсом электрона.
Кинетическая
энергия свободного электрона
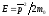 =
= ,
где
,
где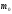 =9,1
10-31 кг
– масса свободного электрона.
=9,1
10-31 кг
– масса свободного электрона.
В
1926 г. австрийский физик Эрвин Шрёдингер
вывел уравнение для волн де Бройля.
Волна, связанная с отдельной частицей
описывается
волновой функцией
 ,
то есть зависящей от координат и времени.
,
то есть зависящей от координат и времени.
|
|
(1.1) |
В
левой части – скорость изменения
волновой функции, умноженная на мнимую
единицу (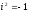 )
и приведенную постоянную Планка. В
правой –оператор
Гамильтона
Ĥ,
действующий
на волновую функцию. Оператор полной
энергии (гамильтониан) Ĥ
получается
из выражения
)
и приведенную постоянную Планка. В
правой –оператор
Гамильтона
Ĥ,
действующий
на волновую функцию. Оператор полной
энергии (гамильтониан) Ĥ
получается
из выражения
|
|
(1.2) |
где E – собственная энергия частицы (системы частиц).
Энергия
частицы массой
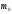 имеет две составляющие – кинетическую
и потенциальную:
имеет две составляющие – кинетическую
и потенциальную:
|
|
(1.3) |
Кинетическая
энергия
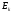 =
=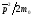 .
Если заменить в правой части уравнения
величину импульса
.
Если заменить в правой части уравнения
величину импульса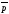 на так называемый оператор импульса,
на так называемый оператор импульса,
 ,где
,где
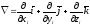 -
оператор Гамильтона или набла- оператор,
получим:
-
оператор Гамильтона или набла- оператор,
получим:
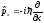 ,
,
 ,
,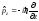 .
.
Тогда уравнение (1.2) можно переписать в виде:
|
|
(1.4) |
-
уравнение Шредингера для свободной
частицы.
Здесь
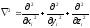 -
оператор Лапласа.
-
оператор Лапласа.
Решение такого уравнения для частицы, движущейся по оси x имеет вид:
|
|
(1.5) |
т.е. волновые функции свободной частицы есть плоские волны.
В любой момент времени t, состояние квантовой частицы задается двумя величинами: координатами (радиусом-вектором) и импульсом:
|
|
(1.6) |
Учитывая,
что
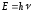 =
=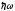 - энергия свободного электрона,
- энергия свободного электрона,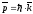 - импульс свободного электрона, можно
записать уравнение для волновой функции
в следующем виде:
- импульс свободного электрона, можно
записать уравнение для волновой функции
в следующем виде:
|
|
(1.7) |
Здесь

 - циклическая частота. Это - комплексная
синусоида.Групповая
скорость
волнового пакета
- циклическая частота. Это - комплексная
синусоида.Групповая
скорость
волнового пакета
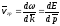 .
.
Если
нам известна волновая функция, то из
нее можно получить энергию, продифференцировав
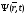 по времени
один раз и квадрат импульса продифференцировав
по времени
один раз и квадрат импульса продифференцировав
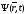 по координате
дважды:
по координате
дважды:
|
|
(1.8) |
В
самом деле, из найденных формул выразим
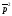 иE,
подставим их в уравнение Шредингера,
тогда получим тождество:
иE,
подставим их в уравнение Шредингера,
тогда получим тождество:
|
|
(1.9) |
Но
как определить саму волновую функцию?
Тем более, что в соответствии с соотношением
неопределенностей немецкого физика
Вернера Гейзенберга, выведенного им в
1927 г. координату и импульс любой
микрочастицы нельзя измерить точно
одновременно:
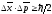 (для одномерного движения, чем точнее
значение координаты, тем менее точно
можно измерить значение импульса).
Максимум, что можно сделать – это
определить три координаты или три
компоненты импульса, а затем из уравнения
Шрёдингера вычислить волновую функцию
в какой угодно последующий момент
времени. То есть при решении конкретных
задач уравнение Шредингера должно быть
дополнено заданием начальных условий:
для момента времениt=0,
т.е. нужно задать функцию
(для одномерного движения, чем точнее
значение координаты, тем менее точно
можно измерить значение импульса).
Максимум, что можно сделать – это
определить три координаты или три
компоненты импульса, а затем из уравнения
Шрёдингера вычислить волновую функцию
в какой угодно последующий момент
времени. То есть при решении конкретных
задач уравнение Шредингера должно быть
дополнено заданием начальных условий:
для момента времениt=0,
т.е. нужно задать функцию
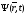 =
=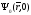 .
.
Так
что такое волновая функция? В 1926 г.
немецкий физик Макс Борн предложил, что
волновая функция
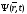 физического смысла не имеет, но
определяет
вероятность пребывания электрона в
заданной точке. В тех областях, где
амплитуда волны больше, обнаружение
электрона более вероятно, то есть |
физического смысла не имеет, но
определяет
вероятность пребывания электрона в
заданной точке. В тех областях, где
амплитуда волны больше, обнаружение
электрона более вероятно, то есть |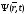 |2
dV
– вероятность
обнаружить данную частицу в объеме dV.
|2
dV
– вероятность
обнаружить данную частицу в объеме dV.
|
|
(1.10) |
здесь
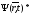 - комплексно-сопряженная с функцией
- комплексно-сопряженная с функцией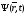 .
.
|
|
(1.11) |

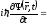 Ĥ
Ĥ
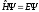 ,
,
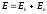 .
. ,
,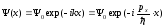 ,
,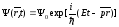 ,
,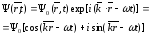 ,
,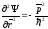 ,
,
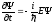
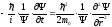 .
.
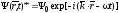 .
.