- •Глава 1. Математическая формулировка задачи непрерывной оптимизации в конечномерном пространстве
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения
- •Глава 12. Задачи оптимального управления и методы их приближенного решения
- •Глава 1. Математическая формулировка задачи оптимального проектирования.
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации.
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения.
- •Глава 4. Методы поиска локального минимума одномерных функций.
- •Глава 5. Методы поиска глобального минимума одномерных функций.
- •Глава 6. Многомерная локальная безусловная оптимизация. Детерминированные прямые методы.
- •Глава 7. Многомерная локальная безусловная оптимизация. Детерминированные методы первого и второго порядков.
- •1. Постановка задачи.
- •2. Итерационная формула.
- •Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска (прямые методы).
- •Глава 9. Многомерная локальная условная оптимизация.
- •Глава 10. Многомерная глобальная условная оптимизация.
- •Глава 11. Задачи многокритериальной оптимизации и методы их решения.
- •Глава 12. Задачи оптимального управления и методы их приближенного решения.
Глава 7. Многомерная локальная безусловная оптимизация. Детерминированные методы первого и второго порядков.
7.1 Метод наискорейшего спуска. Метод дробления шага
Рассматривается
следующая многомерная задача
локальной безусловной оптимизации:
найти минимумкритерия
оптимальности
![]() (
(![]() ),
определенного в
),
определенного в
![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве
![]() ,
,
|
|
(1) |
Положим,
что функция
![]() (
(![]() )
всюду дифференцируема в
)
всюду дифференцируема в
![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве
![]() .
.
Направление
спуска в градиентных
методах оптимизациисовпадает с
направлением антиградиента минимизируемой
функции
![]() (
(![]() ).
Итерационная формула градиентных
методов оптимизации имеет вид
).
Итерационная формула градиентных
методов оптимизации имеет вид
|
|
(2) |
Здесь
![]() -
длина шага на
-
длина шага на
![]() -ой
итерации в направлении
-ой
итерации в направлении
![]() ,
где
,
где
|
|
(3) |
единичный
вектор направления антиградиента
функции
![]() (
(![]() )
в точке
)
в точке
![]() ,
,
![]() -
некоторая векторная норма, например,
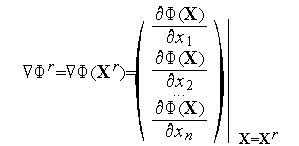
евклидова. Напомним, что градиент функции
-
некоторая векторная норма, например,
евклидова. Напомним, что градиент функции
![]() (
(![]() )
в точке
)
в точке
![]() есть
значение вектора частных производных
этой функции в точке
есть
значение вектора частных производных
этой функции в точке
![]() :
:
Различные
градиентные
методы оптимизацииотличаются между
собой правилами выбора длины шага
![]() .
.
Градиентный метод наискорейшего спуска.
Градиентный
метод наискорейшего спускав качестве
длины шага
![]() использует
величину, при которой достигается
минимум функции
использует
величину, при которой достигается
минимум функции
![]() (
(![]() )
в направлении
)
в направлении
![]() :
:
|
|
(4) |
Задача (2) есть одномерная задача локальной безусловной оптимизации, которая может быть решена рассмотренными в главе 4 методами, например,методом Паулла(см. параграф 4.7).
Схема метода:
Задаем начальную точку
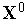 и
полагаем счетчик числа итераций
и
полагаем счетчик числа итераций
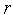 =0.
=0.По формуле (3) вычисляем компоненты вектора
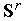 .
.Каким-либо методом решаем одномерную задачу безусловной оптимизации(4) – определяем точку
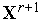 .
.Вычисляем величину
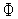 (
(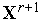 )
- значение функции
)
- значение функции
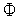 (
(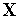 )
в точке
)
в точке
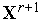 .
.Проверяем условие окончания поиска (см. ниже). Если условие окончания поиска выполнено, то полагаем
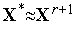 и
завершаем итерации. Иначе – полагаем
и
завершаем итерации. Иначе – полагаем
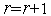 ,
переходим к п. 2
,
переходим к п. 2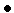
В качестве критерия окончания поиска можно использоваться одно из стандартных условий окончания итераций
|
|
(5) |
|
|
(6) |
В качестве критерия окончания поиска можно использоваться также условие
|
|
(7) |
где
![]() -
константа, определяющая требуемую
точность решения по градиенту функции
-
константа, определяющая требуемую
точность решения по градиенту функции
![]() (
(![]() ).
).
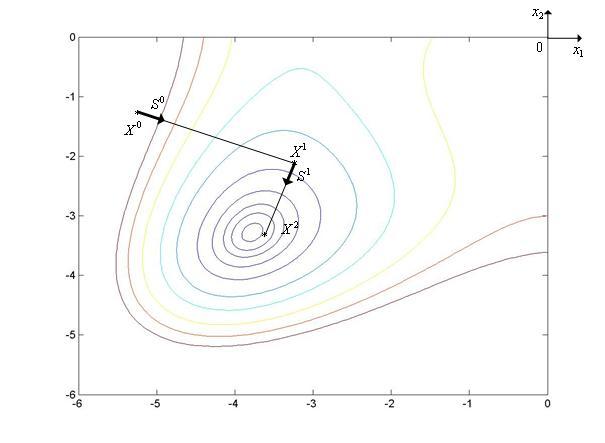
Градиентный метод наискорейшего спускаиллюстрирует рис. 1, на котором показан фрагмент линий уровняфункции Химмельблау.
|
|
Рис. 1. Траектория поиска минимума функции Химмельблау градиентным методом наискорейшего спуска.
Градиентный метод с дроблением шага
В
градиентном
методе с дроблением шагаточка
![]() определяется
по формуле
определяется
по формуле
|
|
(8) |
где
величина шага
![]() находится
из условия
находится
из условия
|
|
(9) |
Схема метода:
Задаем начальную точку
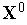 ,
начальную величину шага
,
начальную величину шага
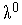 и
коэффициент дробления шага
и
коэффициент дробления шага
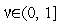 .
Полагаем счетчик числа итераций
.
Полагаем счетчик числа итераций
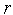 =0.
=0.По формуле (8) вычисляем компоненты вектора
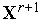 .
.Вычисляем величину
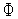 (
(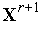 )
- значение функции
)
- значение функции
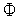 (
(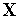 )
в точке
)
в точке
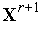 .
.Если условие (9) выполнено, то переходим к следующему пункту. Иначе – переходим к пункту 6.
Полагаем
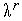 =
=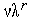 и переходим к пункту 2.
и переходим к пункту 2.Проверяем условие окончания поиска (см. ниже). Если условие окончания поиска выполнено, то полагаем
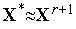 ,
и завершаем итерации. Иначе – полагаем
,
и завершаем итерации. Иначе – полагаем
 =
=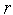 +1
переходим к п. 2
+1
переходим к п. 2
В качестве критерия окончания поиска можно использоваться условия (5) – (7).
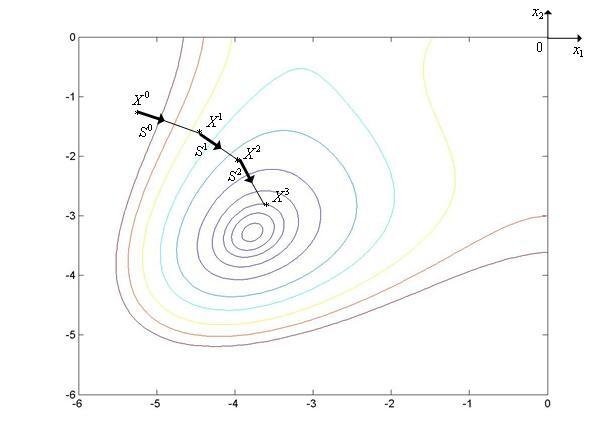
Градиентный метод дробления шага иллюстрирует рис. 2, на котором показан фрагмент линий уровня функции Химмельблау.
|
|
Рис. 2. Траектория поиска минимума функции Химмельблау градиентным методом дробления шага.
Пример 1