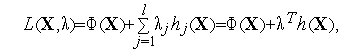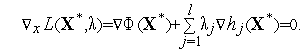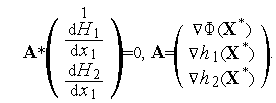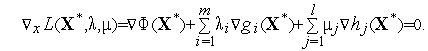- •Глава 1. Математическая формулировка задачи непрерывной оптимизации в конечномерном пространстве
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения
- •Глава 12. Задачи оптимального управления и методы их приближенного решения
- •Глава 1. Математическая формулировка задачи оптимального проектирования.
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации.
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения.
- •Глава 4. Методы поиска локального минимума одномерных функций.
- •Глава 5. Методы поиска глобального минимума одномерных функций.
- •Глава 6. Многомерная локальная безусловная оптимизация. Детерминированные прямые методы.
- •Глава 7. Многомерная локальная безусловная оптимизация. Детерминированные методы первого и второго порядков.
- •1. Постановка задачи.
- •2. Итерационная формула.
- •Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска (прямые методы).
- •Глава 9. Многомерная локальная условная оптимизация.
- •Глава 10. Многомерная глобальная условная оптимизация.
- •Глава 11. Задачи многокритериальной оптимизации и методы их решения.
- •Глава 12. Задачи оптимального управления и методы их приближенного решения.
Глава 2. Условия существования минимума в детерминированных задачах оптимизации.
2.1 Одномерная задача оптимизации
Рассмотрим
задачу поиска минимума одномерной
функции
![]() (
(![]() ),
определенной на интервале
),
определенной на интервале
![]() :
:
![]()
Как
известно из курса математического
анализа, внутренние точки локального
и глобального минимума функции
![]() (
(![]() )
являются стационарными
точками критерия оптимальности
)
являются стационарными
точками критерия оптимальности
![]() (
(![]() )
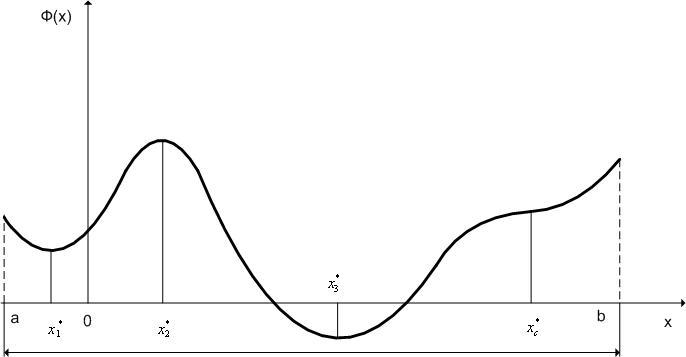
(см. рис. 1) или, что то же самое, решениями
уравнения
)
(см. рис. 1) или, что то же самое, решениями
уравнения
|
|
(1) |
|
|
Рис. 1. Локальные минимумы(x1*,x3*), локальный максимум (x2*) и точка перегиба (xc*) функции Φ(x).
Но,
решениями уравнения (1) являются не
только точки минимума, но и точки
максимума и точки перегиба функции
![]() (
(![]() )
(см. рис. 1). Следовательно, уравнение
(1) является только необходимым условием
минимума, но не является достаточным
условием.
)
(см. рис. 1). Следовательно, уравнение
(1) является только необходимым условием
минимума, но не является достаточным
условием.
Если
существует вторая производная функции
![]() (
(![]() ),
то для отыскания достаточных условий
минимума
),
то для отыскания достаточных условий
минимума
![]() (
(![]() )
можно привлечь эту производную. Из курса
математического анализа известно, что
если в точке
)
можно привлечь эту производную. Из курса
математического анализа известно, что
если в точке
![]() значение
первой производной функции
значение
первой производной функции
![]() (
(![]() )
равно нулю, а второй производной –
положительно, то в этой точке функция
)
равно нулю, а второй производной –
положительно, то в этой точке функция
![]() (
(![]() )
имеет минимум (локальный или глобальный).
)
имеет минимум (локальный или глобальный).
Таким образом, имеем следующую теорему:
Теорема
1.
Если функция
![]() (
(![]() )
определена и дважды непрерывно
дифференцируема на интервале [
)
определена и дважды непрерывно
дифференцируема на интервале [![]() ,
,![]() ],
то необходимыми и достаточными условиями
минимума этой функции в точке
],
то необходимыми и достаточными условиями
минимума этой функции в точке
![]() являются
условия
являются
условия
![]()
Приведем
доказательство справедливости последнего
условия. Для этого рассмотрим разложение
функции
![]() (
(![]() )
в ряд Тейлора в окрестности точки
)
в ряд Тейлора в окрестности точки
![]() :
:
|
|
(2) |
Здесь
![]() –
некоторая достаточно малая величина.
–
некоторая достаточно малая величина.
Для
того, что в точке
![]() достигался
минимум функции
достигался
минимум функции
![]() (
(![]() ),
необходимо, чтобы разность
),
необходимо, чтобы разность
![]() была
положительной. Поскольку
была
положительной. Поскольку
![]() ,
то из (2) следует, что для выполнения
этого условия необходимо, чтобы имело
место неравенство
,
то из (2) следует, что для выполнения
этого условия необходимо, чтобы имело
место неравенство
![]()
![]()
Точками,
в которых функция
![]() (
(![]() )
принимает наименьшее на интервале
)
принимает наименьшее на интервале
![]() значение,
могут быть либо ее стационарные точки,
лежащие внутри интервала
значение,
могут быть либо ее стационарные точки,
лежащие внутри интервала
![]() ,
либо ее точки недифференцируемости
(критические
точки критерия оптимальности), к
которым следует отнести также концы
интервала
,
либо ее точки недифференцируемости
(критические
точки критерия оптимальности), к
которым следует отнести также концы
интервала
![]() .
.
Поэтому
точку, в которой функция
![]() принимает
наименьшее на интервале
принимает
наименьшее на интервале
![]() значение,
нужно искать, сравнивая значения этой
функции во всех стационарных и критических
точках.
значение,
нужно искать, сравнивая значения этой
функции во всех стационарных и критических
точках.
2.2 Многомерная задача безусловной оптимизации
Многие
методы решения многомерной задачи
нелинейного программированияоснованы
на сведении этой задачи кзадаче
безусловной оптимизации. Поэтому
рассмотрим
![]() -мерную
задачу
оптимизации без ограничений
-мерную
задачу
оптимизации без ограничений
|
|
(1) |
По
аналогии с одномерной задачей, для того,
чтобы точка
![]() являлась
минимумом функции
являлась
минимумом функции
![]() (
(![]() )
необходимо выполнение условия
стационарности функции
)
необходимо выполнение условия
стационарности функции
![]() (
(![]() )
в точке
)
в точке
![]() или,
что то же самое, необходимо, чтобы точка
или,
что то же самое, необходимо, чтобы точка
![]() была
стационарной
точкой функции
была
стационарной
точкой функции
![]() (
(![]() ):
):
|
|
(2) |
Положим,
что функции
![]() (
(![]() )
дважды непрерывно дифференцируема в
окрестности точки
)
дважды непрерывно дифференцируема в
окрестности точки
![]() .
Для поиска достаточного условия
достижения этой функцией в точке
.
Для поиска достаточного условия
достижения этой функцией в точке
![]() минимума,
разложим
минимума,
разложим
![]() (
(![]() )
в окрестности точки
)
в окрестности точки
![]() в
ряд Тейлора:
в
ряд Тейлора:
|
|
(3) |
Здесь
![]() -мерный
вектор-столбец достаточно малых величин
-мерный
вектор-столбец достаточно малых величин
![]() ,
,
![]() –
–
![]() -матрица
Гессе.
-матрица
Гессе.
По
аналогии с одномерной задачей, для того,
что в точке
![]() достигался
минимум функции
достигался
минимум функции
![]() (
(![]() ),
необходимо, чтобы разность
),
необходимо, чтобы разность
![]() была
положительной. Поскольку
была
положительной. Поскольку
![]() ,
то из (3) следует, что для выполнения
этого условия необходимо, чтобы матрица
Гессе
,
то из (3) следует, что для выполнения
этого условия необходимо, чтобы матрица
Гессе
![]() (
(![]() )
была положительно определена в точке
)
была положительно определена в точке
![]() .
.
Таким образом, справедлива
Теорема
1.
Если функция
![]() (
(![]() )
дважды непрерывно дифференцируема в
окрестности точки
)
дважды непрерывно дифференцируема в
окрестности точки
![]() Rn,
то необходимыми и достаточными условиями
минимума этой функция в точке
Rn,
то необходимыми и достаточными условиями
минимума этой функция в точке
![]() являются
условия:
являются
условия:
|
|
(4) |
![]() (
(![]() )
- положительно определена
)
- положительно определена![]()
Таким образом, теорема 1 определяет необходимые и достаточные условия минимума в многомерная задача безусловной оптимизации.
Заметим,
что условие
![]() (
(![]() )=0
является только необходимым
условием минимума в многомерной задаче
безусловной оптимизации.
)=0
является только необходимым
условием минимума в многомерной задаче
безусловной оптимизации.
По
аналогии с одномерной задачей точками,
в которых функция
![]() (
(![]() )
достигает своего наименьшего значения,
могут быть либо ее стационарные
точки функции, либокритические
точки функции(точки недифференцируемости).
)
достигает своего наименьшего значения,
могут быть либо ее стационарные
точки функции, либокритические
точки функции(точки недифференцируемости).
Поэтому
так же, как в одномерной задаче, точку,
в которой функция
![]() (
(![]() )
принимает наименьшее значение нужно
искать, сравнивая значения этой функции
во всех стационарных и критических
точках.
)
принимает наименьшее значение нужно
искать, сравнивая значения этой функции
во всех стационарных и критических
точках.
2.3 Задача выпуклого программирования
Рассмотрим
![]() -мерную
задачу
выпуклого программирования
-мерную
задачу
выпуклого программирования![]()
![]() (
(![]() )
– выпуклая
функция,
)
– выпуклая
функция,
![]() –
выпуклое не пустое ограниченное и
замкнутое множество
допустимых значений вектора варьируемых
переменных. Напомним, что по определению
выпуклая функция является непрерывной.
–
выпуклое не пустое ограниченное и
замкнутое множество
допустимых значений вектора варьируемых
переменных. Напомним, что по определению
выпуклая функция является непрерывной.
Во
внутренних
точках множества допустимых значений
![]() функция
функция
![]() (
(![]() )
достигает минимального значения в
точках, которые являются ее либо
стационарными
точками функции, либокритическими
точками функции. Однако функция может
достигать своего наименьшего значения
и вграничных
точках
области определения
)
достигает минимального значения в
точках, которые являются ее либо
стационарными
точками функции, либокритическими
точками функции. Однако функция может
достигать своего наименьшего значения
и вграничных
точках
области определения
![]() .
.
Важные свойства задачи выпуклого программированияопределяют две следующие теоремы.
Теорема
1.
Если внутренняя точка
![]() множества
множества
![]() является
точкой локального минимума в задаче
выпуклого программирования, то в этой
точке функция
является
точкой локального минимума в задаче
выпуклого программирования, то в этой
точке функция
![]() достигает
глобального минимума.
достигает
глобального минимума.
Доказательство.
Положим, что в точке
![]() функция
функция
![]() не
достигает наименьшего во множестве
не
достигает наименьшего во множестве
![]() значения.
Тогда существует точка
значения.
Тогда существует точка
![]() ,
для которой
,
для которой
![]() .
Рассмотрим сечение
.
Рассмотрим сечение
![]() .
Функция
.
Функция
![]() (
(![]() )
достигает в точке
)
достигает в точке
![]() =0
наибольшее значение. Действительно,
поскольку
=0
наибольшее значение. Действительно,
поскольку
![]()
Это
значит, что существует окрестность
![]() точки
точки
![]() и
некоторое
и
некоторое
![]() такие,
что
такие,
что
![]() .
Но тогда
.
Но тогда
![]() ,
что противоречит условию теоремы
,
что противоречит условию теоремы
Из теоремы следует, что во всех точках локального минимума выпуклая функцияимеете одинаковые значения.
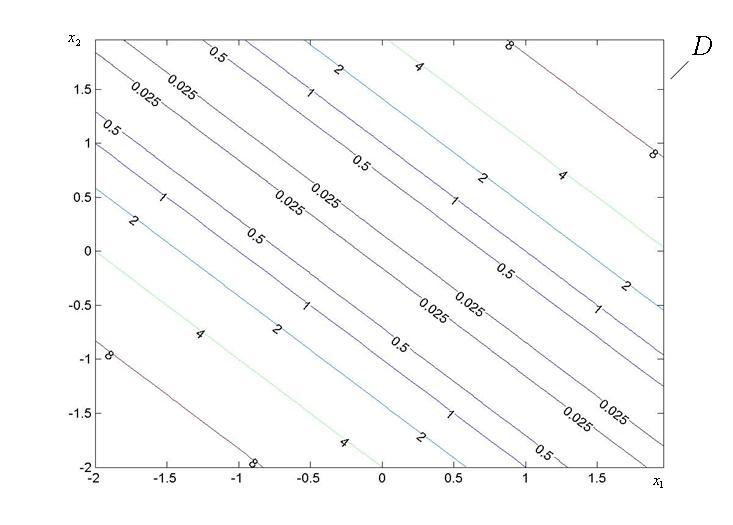
Пример 1
Рассмотрим
не строго выпуклую квадратичную функцию
![]() ,
определенную в области
,
определенную в области
![]() =
=![]() (см. рис. 1). Все локальные минимумы
этой функции равны нулю и расположены
на прямой -
(см. рис. 1). Все локальные минимумы
этой функции равны нулю и расположены
на прямой -![]() +
+![]() =0
.
=0
.
MATLAB-программа:
x=-2:0.06:2;
y=x;
[X,Y]=meshgrid(x);
Z=(X+Y).^2;
V=[0.025,0.5,1,2,4,8];
[C,h]=contour(X,Y,Z,V);
clabel(C,h);
|
|
Рис. 1. К прим. 1
Теорема
2.
Функция
![]() (
(![]() ),
строго
выпуклая функциянавыпуклом
множестве, имеет в этом множестве не
более одной точки минимума (глобального)
),
строго
выпуклая функциянавыпуклом
множестве, имеет в этом множестве не
более одной точки минимума (глобального)![]()
Условие существования решения задачи выпуклого программированиядает следующая теорема.
Теорема
3.
Пусть функция
![]() (
(![]() )
выпукла на выпуклом
множестве
)
выпукла на выпуклом
множестве
![]() и
дифференцируема в точке
и
дифференцируема в точке
![]() Тогда
для того чтобы эта точка была точкой
минимума функции
Тогда
для того чтобы эта точка была точкой
минимума функции
![]() (
(![]() ),
необходимо и достаточно, чтобы для любой
точки
),
необходимо и достаточно, чтобы для любой
точки
![]() выполнялось
неравенство
выполнялось
неравенство
|
|
(1) |
Необходимость.
Рассмотрим сечение
![]() функции
функции
![]() (
(![]() ).
Функция
).
Функция
![]() (
(![]() )
определена на отрезке [0,1], имеет в точке
)
определена на отрезке [0,1], имеет в точке
![]() =0
локальный минимум и дифференцируема в
этой точке. Следовательно
=0
локальный минимум и дифференцируема в
этой точке. Следовательно
![]() (равенство
нулю имеет место в том случае, когда
точка
(равенство
нулю имеет место в том случае, когда
точка
![]() является
внутренней точкой множества
является
внутренней точкой множества
![]() ).
По правилу дифференцирования сложной
функции
).
По правилу дифференцирования сложной
функции
![]()
Достаточность.
Пусть в точке
![]() выполнено
неравенство (1). Рассмотрим сечение
выполнено
неравенство (1). Рассмотрим сечение
![]() функции
функции
![]() (
(![]() ),
где
),
где
![]() –
произвольная точка из множества
–
произвольная точка из множества
![]() .
Поскольку
.
Поскольку
![]() (
(![]() )
выпукла во множестве
)
выпукла во множестве
![]() ,
то функция
,
то функция
![]() (
(![]() )
также выпукла на отрезке [0,1]. Кроме того,
из неравенства (1) следует, что
)
также выпукла на отрезке [0,1]. Кроме того,
из неравенства (1) следует, что
![]() (0)
(0)![]() 0.
Это означает, что
0.
Это означает, что
![]() (
(![]() )
- неубывающая отрезке [0,1] функция, т.е.
)
- неубывающая отрезке [0,1] функция, т.е.
![]() (0)
(0)![]() (1).
Последнее неравенство означает, что
(1).
Последнее неравенство означает, что
![]() и
в точке
и
в точке
![]() функция
функция
![]() (
(![]() )
принимает наименьшее в области
)
принимает наименьшее в области
![]() значение
значение![]()
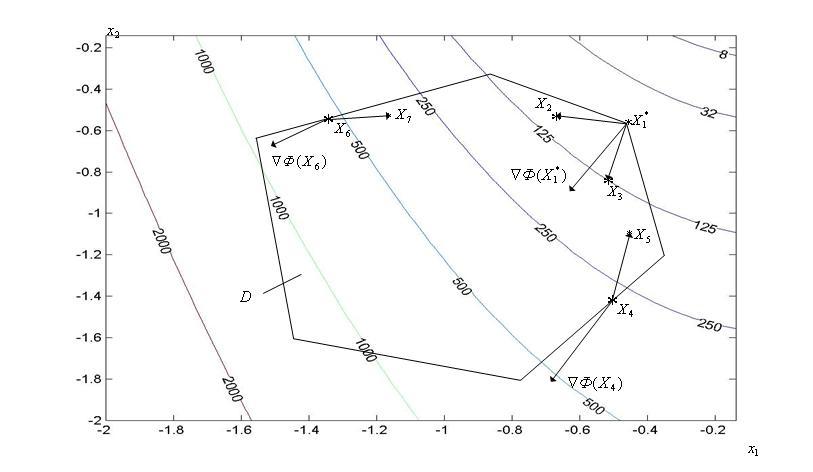
Теорему 3 иллюстрирует рис. 2, линии уровня на котором получены с помощью следующей MATLAB-программы:
x=-2:0.06:-0.1;
y=x;
[X,Y]=meshgrid(x);
Z=100.*(Y-X.^2).^2+(1-X).^2;
V=[2,8,32,125,250,500,1000,2000];
contour(X,Y,Z,V);
[C,h]=contour(X,Y,Z,V);
clabel(C,h);
Точка![]() на рис.рис. 2 является точкой локального
минимума, поскольку не существует такой
точки
на рис.рис. 2 является точкой локального
минимума, поскольку не существует такой
точки
![]() ,
что скалярное произведение (
,
что скалярное произведение (![]() (
(![]() ),(
),(![]() -
-![]() ))
отрицательно. Точка
))
отрицательно. Точка
![]() ,
например, не является точкой локального
минимума, так как существуют такие точки
,
например, не является точкой локального
минимума, так как существуют такие точки
![]() ,
что скалярное произведение (
,
что скалярное произведение (![]() (
(![]() ),(
),(![]() -
-![]() ))
отрицательно.
))
отрицательно.
|
|
Рис. 2. К теореме 3.
Заметим,
что если точка
![]() является
внутренней точкой множества
является
внутренней точкой множества
![]() ,
то условие (1) эквивалентно условию
,
то условие (1) эквивалентно условию
![]() .
Таким образом, условие (1) можно
рассматривать как обобщение необходимого
условия минимума в многомерной задаче
безусловной оптимизации.
.
Таким образом, условие (1) можно
рассматривать как обобщение необходимого
условия минимума в многомерной задаче
безусловной оптимизации.
2.4 Задача нелинейного программирования с ограничениями типа равенств
Рассмотрим
![]() -мерную
задачу
нелинейного программирования
-мерную
задачу
нелинейного программирования
|
|
(1) |
где
|
|
(2) |
-не пустое, ограниченное замкнутое множество.
Нам понадобятся далее понятия множителей Лагранжаифункции Лагранжа.Функция Лагранжадля задачи (1) с ограничениями (2) определяется формулой
|
|
(3) |
где
![]() -
-
![]() -вектор
множителей
Лагранжа.
-вектор
множителей
Лагранжа.
Нам
понадобится также понятие условия
регулярности ограничивающих функций.
Если точка
![]() ,
то условие линейной независимости
векторов
,
то условие линейной независимости
векторов
![]() называется
условием регулярности задачи (1), (2) в
точке
называется
условием регулярности задачи (1), (2) в
точке
![]() .
Данное условие означает, в частности,
что количество ограничивающих
функций, проходящих через точку
.
Данное условие означает, в частности,
что количество ограничивающих
функций, проходящих через точку
![]() ,
не может быть больше размерности вектора
варьируемых параметров, т.е. должно
быть выполнено неравенство
,
не может быть больше размерности вектора
варьируемых параметров, т.е. должно
быть выполнено неравенство
![]() .
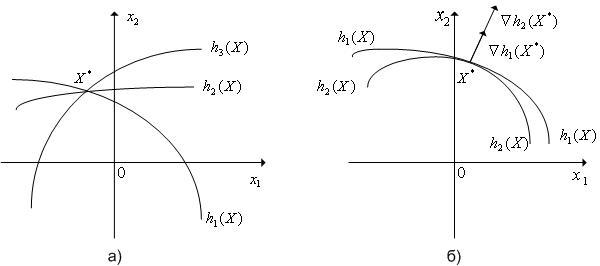
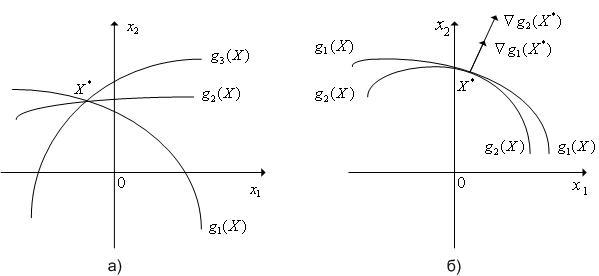
Например, на рис. 1 в ситуации (а)
количество ограничивающих функций,
проходящих через точку
.
Например, на рис. 1 в ситуации (а)
количество ограничивающих функций,
проходящих через точку
![]() ,
превышает размерность вектора варьируемых
параметров, в ситуации (б) в точке
,
превышает размерность вектора варьируемых
параметров, в ситуации (б) в точке
![]() градиенты
градиенты
![]() (
(![]() ),
),
![]() (
(![]() )
ограничивающих функций коллениарны.
)
ограничивающих функций коллениарны.
|
|
Рис. 1. Ситуации, в которых в двумерном случае (n=2) не выполняется условие регулярности системы функций h(X) в точке X*.
Исключительно важное место в теории и практике решения задач нелинейного программирования с ограничениями типа равенствзанимает следующая теорема (правило Лагранжа для задачи оптимизации с ограничениями типа равенств).
Теорема
1.
Пусть функция
![]() и
функции
и
функции
![]() имеют
непрерывные частные производные в
некоторой окрестности точки
имеют
непрерывные частные производные в
некоторой окрестности точки
![]() и
пусть эта точка является точкой локального
минимума функции
и
пусть эта точка является точкой локального
минимума функции
![]() при
условии
при
условии
![]() .
Пусть, кроме того, выполняется условие
регулярности системы функций
.
Пусть, кроме того, выполняется условие
регулярности системы функций
![]() в
точке
в
точке
![]() .
Тогда существуют такие множители
Лагранжа
.
Тогда существуют такие множители
Лагранжа
![]() ,
,![]() [1,
[1,![]() ],
не
все из которых равные нулю одновременно,
что для функции
Лагранжа
],
не
все из которых равные нулю одновременно,
что для функции
Лагранжа
![]() точка
точка
![]() является
стационарной
точкой функции, т.е.
является
стационарной
точкой функции, т.е.
|
|
(4) |
Доказательство
теоремы приведем для одного частного
случая. Пусть
![]() =3,
т.е. минимизируемая функция
=3,
т.е. минимизируемая функция
![]() ,
и пусть заданы два ограничения типа
равенств
,
и пусть заданы два ограничения типа
равенств
|
|
(5) |
Ограничения
(5) определяют область допустимых значений
![]() ,
которая представляет собой некоторую
кривую в пространстве
,
которая представляет собой некоторую
кривую в пространстве
![]() ,
являющуюся результатом пересечения
поверхностей
,
являющуюся результатом пересечения
поверхностей
![]() ,
,
![]() .
Допустим, что функция
.
Допустим, что функция
![]() (
(![]() )
имеет точку локального минимума
)
имеет точку локального минимума
![]() в
области
в
области
![]() .
Допустим также, что выполнены условия
теоремы 1, т.е. функции
.
Допустим также, что выполнены условия
теоремы 1, т.е. функции
![]() (
(![]() ),
),
![]() имеют
непрерывные частные производные в
некоторой окрестности точки
имеют
непрерывные частные производные в
некоторой окрестности точки
![]() и
градиенты функций
и
градиенты функций
![]() в
этой точке линейно независимы. Положим,
кроме того, что из равенств (5) переменные
в
этой точке линейно независимы. Положим,
кроме того, что из равенств (5) переменные
![]() ,
,
![]() можно
выразить через переменную
можно
выразить через переменную
![]() в
виде
в
виде
|
|
(6) |
Подставив
выражения (6) в выражение для функции
![]() (
(![]() ),
преобразуем исходную задачу к следующей
задаче
оптимизации без ограничений, которая
содержит только одну переменную
),
преобразуем исходную задачу к следующей
задаче
оптимизации без ограничений, которая
содержит только одну переменную
![]() :
:
|
|
(7) |
Поскольку
функция
![]() (
(![]() )
имеет точку минимума
)
имеет точку минимума
![]() ,
производная по
,
производная по
![]() функции
функции
![]() в
точке
в
точке
![]() равна
нулю:
равна
нулю:
|
|
(8) |
Дифференцируя
по
![]() выражения
(5), получим
выражения
(5), получим
|
|
(9) |
Запишем уравнения (8), (9) в виде матричного уравнения
|
|
(10) |
Поскольку
вектор
![]() не
нулевой, то равенство (10) возможно лишь
в том случае, когда
не
нулевой, то равенство (10) возможно лишь
в том случае, когда
![]() .
Но это возможно лишь в том случае, когда
вектора-строки матрицы
.
Но это возможно лишь в том случае, когда
вектора-строки матрицы
![]() линейно
зависимы. Значит, существуют такие
скаляры
линейно
зависимы. Значит, существуют такие
скаляры
![]() ,
не все равные нулю, что
,
не все равные нулю, что
|
|
(11) |
В
выражении (11) скаляр a не может быть равен
нулю, поскольку противное означало бы
линейную зависимость векторов
![]() ,
,
![]() что
противоречит условию теоремы. Поэтому
после деления на
что
противоречит условию теоремы. Поэтому
после деления на
![]() из
(11) получим
из
(11) получим
![]()
Таким
образом, для рассматриваемого частного
случая справедливость теоремы доказана![]()
Отметим,
что теорема 1 не требует знакоопределенности
(т.е. положительности или отрицательности)
множителей
Лагранжа
![]() .
Теорема требуется лишь того, чтобы не
все из этих множителей равнялись нулю
одновременно.
.
Теорема требуется лишь того, чтобы не
все из этих множителей равнялись нулю
одновременно.
Пример 1
Рассмотрим
в качестве минимизируемой функции
![]() (
(![]() )
функцию
Розенброка
)
функцию
Розенброка
![]() (
(![]() =2).
Положим, что имеется только одно
ограничение типа равенств, которое
задается с помощью функции
=2).
Положим, что имеется только одно
ограничение типа равенств, которое
задается с помощью функции
![]() (
(![]() )=
)=![]() +
+![]() +0.2=0.
Легко видеть, что градиенты функций
+0.2=0.
Легко видеть, что градиенты функций
![]() (
(![]() ),
),
![]() (
(![]() )
равны, соответственно
)
равны, соответственно
![]()
![]()
Задачу иллюстрирует рис. 2, линии уровня функции Розенброкана котором получены с помощью следующей MATLAB-программы:
x=-2:0.06:0;
y=x;
[X,Y]=meshgrid(x);
Z=100.*(Y-X.^2).^2+(1-X).^2;
V=[2,8,32,125,250,500,1000,2000];
contour(X,Y,Z,V);
[C,h]=contour(X,Y,Z,V);
clabel(C,h);
|
В
точках
|
Рис. 2. K прим. 1.
Теорема 1 означает, что в ее условиях вместо задачи условной оптимизации(1), (2) можно решатьзадачу безусловной оптимизации
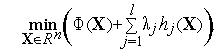
Необходимым
условием существования локального
минимума этой задачи в некоторой точке
![]() является
условие
является
условие
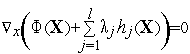 (см.
Теорему 2.1).
(см.
Теорему 2.1).
Широко известна другая форма теоремы 1, которую мы сформулируем в виде следствия этой теоремы.
Следствие.
В условиях теоремы 1 существуют такие
множители
Лагранжа
![]() ,
не
все из которых равные нулю одновременно,
что имеют место следующие равенства:
,
не
все из которых равные нулю одновременно,
что имеют место следующие равенства:
|
|
(12) |
|
|
(13) |
Здесь
равенство (12) повторяет равенство (4), а
справедливость равенства (13) следует
из того факта, что по условиям теоремы
точка
![]() удовлетворяет
всем ограничениям, т.е.
удовлетворяет
всем ограничениям, т.е.
![]() .
.
Заметим,
что из (13) следует справедливость еще
одного полезного равенства
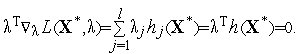
2.5 Теорема Куна-Таккера для задачи нелинейного программирования с ограничениями типа неравенств
Рассмотрим задачу нелинейного программирования
|
|
(1) |
где
![]() (
(![]() )
– произвольная функция,
)
– произвольная функция,
![]()
не пустое, ограниченное замкнутое множество.
Нам понадобятся далее понятия множителей Лагранжаи функции Лагранжа длязадачи нелинейного программирования с ограничениями типа неравенств.Функция Лагранжадля задачи (1) с ограничениями (2) определяется формулой
|
|
(2) |
где
![]() -
-
![]() -вектор
множителей
Лагранжа.
-вектор
множителей
Лагранжа.
Нам
понадобятся также понятия активных и
неактивных ограничений. В точке локального
минимума задачи (1), (2) каждое из ограничений
![]() выполняется
либо в виде равенства
выполняется
либо в виде равенства
![]() ,
либо в виде неравенства
,
либо в виде неравенства
![]() .
Ограничения первого вида называются
активными
ограничениями. Остальные ограничения
называютсянеактивными
ограничениями.
.
Ограничения первого вида называются
активными
ограничениями. Остальные ограничения
называютсянеактивными
ограничениями.
Кроме
того, нам понадобится также понятие
условия регулярности для задачи
нелинейного программирования с
ограничениями типа неравенств. Если
точка
![]() и
ограничения
и
ограничения
![]() активны,
то условие линейной независимости
векторов называется условием
регулярности ограничивающих функций
активны,
то условие линейной независимости
векторов называется условием
регулярности ограничивающих функций
![]() в
точке
в
точке
![]() .
Это условие означает, что, например, при
.
Это условие означает, что, например, при
![]() =2
количество ограничивающих
функций, проходящих через точку
=2
количество ограничивающих
функций, проходящих через точку
![]() ,
не должно превышать 2 и в точке
,
не должно превышать 2 и в точке
![]() векторы
векторы
![]() (
(![]() ),
),
![]() (
(![]() )
не должны быть коллениарны Например,
на рис. 1 в ситуации (а) количество
ограничивающих функций, проходящих
через точку
)
не должны быть коллениарны Например,
на рис. 1 в ситуации (а) количество
ограничивающих функций, проходящих
через точку
![]() ,
превышает размерность вектора
варьируемых параметров, в ситуации
(б) в точке
,
превышает размерность вектора
варьируемых параметров, в ситуации
(б) в точке
![]() градиенты
градиенты
![]() (
(![]() ),
),
![]() (
(![]() )
ограничивающих функций коллениарны.
)
ограничивающих функций коллениарны.
|
|
Рис. 1. Ситуации, в которых не выполняется условие регулярности двумерной задачи.
Исключительно большое значение в теории и практике решения задач нелинейного программированияимеет следующая теорема (теорема Куна-Таккера для задачи условной оптимизации с ограничениями типа неравенств).
Теорема
1 (Куна-Таккера).
Пусть функция
![]() и
функции
и
функции
![]() имеют
непрерывные частные производные в
некоторой окрестности точки
имеют
непрерывные частные производные в
некоторой окрестности точки
![]() и
пусть эта точка является точкой локального
минимума функции
и
пусть эта точка является точкой локального
минимума функции
![]() при
ограничениях
при
ограничениях
![]() ,
удовлетворяющих в точке
,
удовлетворяющих в точке
![]() условию
регулярности ограничивающих функций.
Тогда существуют такие неотрицательныемножители
Лагранжа
условию
регулярности ограничивающих функций.
Тогда существуют такие неотрицательныемножители
Лагранжа
![]() ,
что для функции
Лагранжа
,
что для функции
Лагранжа
![]() точка
точка
![]() является
стационарной
точкой функции, т.е.
является
стационарной
точкой функции, т.е.
|
|
(3) |
Заметим,
что в отличие от правила множителей
Лагранжа, теорема 1 требует
знакоопределенностимножителей
Лагранжа
![]() .
Отметим также, что теорема не запрещает
того, чтобы все множители
Лагранжа
.
Отметим также, что теорема не запрещает
того, чтобы все множители
Лагранжа
![]() были
равны нулю.
были
равны нулю.
Поясним смысл теоремы на примере.
Пример 1
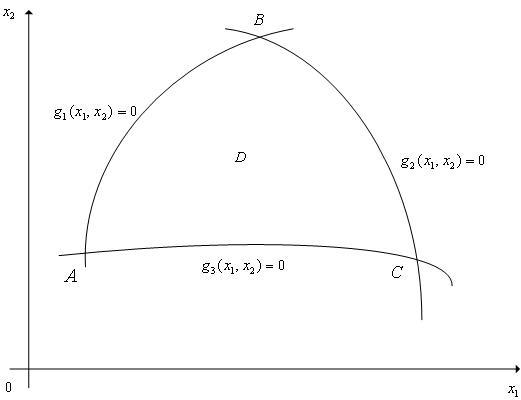
Рассмотрим
двумерную (![]() =2)
задачу
нелинейного программирования(1), (2),
в которой область допустимых значений
=2)
задачу
нелинейного программирования(1), (2),
в которой область допустимых значений
![]() задается
тремя ограничивающими
функциями, т.е.
задается
тремя ограничивающими
функциями, т.е.
![]() .
Положим, что множество
.
Положим, что множество
![]() имеет
вид, представленный на рис. 2.
имеет
вид, представленный на рис. 2.
|
|
Рис. 2. К прим. 1.
Для
всех граничных точек области
![]() ,
очевидно, выполняются условия
регулярности ограничивающих функций.
,
очевидно, выполняются условия
регулярности ограничивающих функций.
Если
точка
![]() находится
внутри множества
находится
внутри множества
![]() (т.е.
является стационарной
точкой функции
(т.е.
является стационарной
точкой функции
![]() )),
то теорема будет справедлива, если
положить все множители
Лагранжа
)),
то теорема будет справедлива, если
положить все множители
Лагранжа
![]() равными
нулю.
равными
нулю.
Пусть
теперь точка
![]() находится
на одной из дуг, например, на дуге AB, т.е.
пусть ограничение
находится
на одной из дуг, например, на дуге AB, т.е.
пусть ограничение
![]() является
активным
ограничением, а остальные ограничения
–неактивными
ограничениями. Тогда в этой точке
является
активным
ограничением, а остальные ограничения
–неактивными
ограничениями. Тогда в этой точке
![]() и
справедливость теоремы вытекает из
правила множителей
Лагранжадля задачи с ограничениями
типа равенств, если положить
и
справедливость теоремы вытекает из
правила множителей
Лагранжадля задачи с ограничениями
типа равенств, если положить
![]() .
.
Пусть,
наконец, точка
![]() находится
в одной из угловых точек множества
находится
в одной из угловых точек множества
![]() ,
например, в точке
,
например, в точке
![]() ,
т.е. пусть ограничения
,
т.е. пусть ограничения
![]() (
(![]() )
)![]() 0,
0,
![]() (
(![]() )
)![]() 0
являются активными
ограничениями, а ограничение
0
являются активными
ограничениями, а ограничение
![]() -
неактивным
ограничением. Тогда можно положить
-
неактивным
ограничением. Тогда можно положить
![]() и
справедливость теоремы вытекает из
правила множителей
Лагранжадля задачи с ограничениями
типа равенств
и
справедливость теоремы вытекает из
правила множителей
Лагранжадля задачи с ограничениями
типа равенств![]()
Теорема
1 означает, что в ее условиях вместо
задачи
условной оптимизации(1), (2) можно
решатьзадачу
безусловной оптимизации![]()
Необходимым
условием существования локального
минимума этой задачи в некоторой точке
![]() является
условие
является
условие
![]() .
(см. Теорему 2.1).
.
(см. Теорему 2.1).
Широко известна другая форма теоремы 1, которую мы сформулируем в виде следствия этой теоремы.
Следствие.
В условиях теоремы 1 существуют такие
неотрицательные множители
Лагранжа
![]() ,
что имеют место следующие равенства:
,
что имеют место следующие равенства:
|
|
(4) |
|
|
(5) |
Здесь
равенство (5) повторяет равенство (4), а
справедливость равенства (6) следует из
того факта, что по условиям теоремы
точка
![]() удовлетворяет
всем ограничениям, т.е.
удовлетворяет
всем ограничениям, т.е.
![]() /
/
Заметим,
что из (6) следует справедливость еще
одного полезного равенства
![]()
2.6 Теорема Куна-Таккера для общей задачи нелинейного программирования
Рассмотрим общую задачу нелинейного программирования
|
|
(1) |
где
![]() –
произвольная функция,
–
произвольная функция,
|
|
(2) |
не пустое ограниченное замкнутое множество.
Нам
понадобятся далее понятия множителей
Лагранжаифункции
Лагранжадля общейзадачи
нелинейного программирования.Функция
Лагранжа для задачи (1) с ограничениями
(2) определяется формулой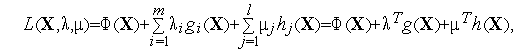
где
![]() ,
,
![]() -
-
![]() -и
-и
![]() -
векторы множителей
Лагранжа, соответственно.
-
векторы множителей
Лагранжа, соответственно.
Нам
понадобится также понятие условий
регулярности для общей задачи
нелинейного программирования. Если
точка
![]() и
ограничения
и
ограничения
![]() являются
активными
ограничениями, то условие линейной
независимости векторов
являются
активными
ограничениями, то условие линейной
независимости векторов
![]() ,
а также условие линейной независимости
векторов
,
а также условие линейной независимости
векторов
![]() называются
условиями
регулярности ограничивающих функцийв точке
называются
условиями
регулярности ограничивающих функцийв точке
![]() .
Смысл условий регулярности раскрыт в
предыдущих параграфах.
.
Смысл условий регулярности раскрыт в
предыдущих параграфах.
Теорема
1 (теорема
Куна-Таккера). Пусть функции
![]() ,
,
![]() ,
,
![]() имеют
непрерывные частные производные в
некоторой окрестности точки
имеют
непрерывные частные производные в
некоторой окрестности точки
![]() и
пусть эта точка является точкой локального
минимума функции
и
пусть эта точка является точкой локального
минимума функции
![]() .
Пусть, кроме того, выполняются условия
регулярности ограничивающих функций
.
Пусть, кроме того, выполняются условия
регулярности ограничивающих функций
![]() ,
,
![]() в
точке
в
точке
![]() .
Тогда существуют такие множители
Лагранжа
.
Тогда существуют такие множители
Лагранжа
![]() ,
,
![]() ,
не все из которых равные нулю одновременно,
что для функции
Лагранжа
,
не все из которых равные нулю одновременно,
что для функции
Лагранжа
![]() точка
точка
![]() является
стационарной
точкой функции, т.е.
является
стационарной
точкой функции, т.е.
|
|
(3) |
Теорема
1 означает, что в ее условиях вместо
задачи
условной оптимизации(1), (2) можно
решатьзадачу
безусловной оптимизации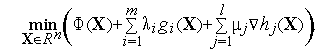
Необходимым
условием существования локального
минимума этой задачи в некоторой точке
![]() является
условие
является
условие
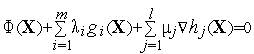 (см.
Теорему 2.1).
(см.
Теорему 2.1).
2.7 Аналитическое решение многомерных задач нелинейного программирования
Ограничимся рассмотрением задачи нелинейного программирования с ограничениями типа неравенств
|
|
(1) |
где
![]() (
(![]() )
– произвольная функция,
)
– произвольная функция,
|
|
(2) |
не пустое, ограниченное замкнутое множество.
Рассмотрим
прямое решение задачи
![]() ,
,
![]() (без
использования теоремы
Куна-Таккера), а также решение этой
задачи на основе использованиятеоремы
Куна-Таккера
(без
использования теоремы
Куна-Таккера), а также решение этой
задачи на основе использованиятеоремы
Куна-Таккера
Прямое решение (без использования теоремы Куна-Таккера).
Общая схема прямого решения задачи нелинейного программирования:
Из условия
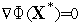 определяем
все стационарные
точки функции
определяем
все стационарные
точки функции
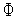
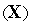 в
области
в
области
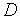 ;
;Определяем все критически точки функции(точки не дифференцируемости) функции
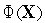 в
области
в
области
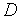 ;
;Для каждой из границ области
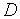 (ограничивающих
функций) решаем соответствующую
задачу на условный минимум:
(ограничивающих
функций) решаем соответствующую
задачу на условный минимум:
из уравнения
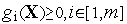 выражаем
выражаем
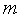 переменных
через остальные
переменных
через остальные
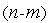 переменных
и подставляем их в выражение для функции
переменных
и подставляем их в выражение для функции
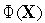 ;
;вместо исходной задачи условной оптимизацииполучаемзадачу безусловной оптимизации
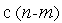 переменными;
переменными;
решаем эту задачу – находим стационарные точки полученной функции, лежащие на соответствующей границе области
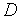 ;.
;.
Решаем
задачу, аналогичную задаче, рассмотренной
в п.3, для каждого из множеств, которое
определяется пересечением границ
области
![]() ;
;
Во
всех отобранных точках вычисляем
значения функции
![]() и
выбираем ту (или те), в которой значение
функции наименьшее
и
выбираем ту (или те), в которой значение
функции наименьшее![]()
Заметим,
что в общем случае такой подход трудно
реализовать на практике, поскольку
далеко не всегда удается разрешить
уравнения
![]() относительно
указанных переменных.
относительно
указанных переменных.
Решение с использованием теоремы Куна-Таккера.
Общая схема решения задачи нелинейного программирования с использованием теоремы Куна-Таккера:
Записываем функцию Лагранжа
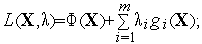
(3)
Находим градиенты
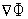 (
(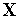 ),
),
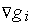 (
(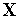 ),
),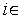 [1,
[1,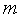 ]
функций
]
функций
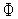 (
(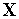 ),
),
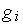 (
(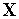 ),
),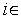 [1,
[1,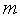 ];
];Находим стационарные точки функции Лагранжа, т.е. точки, в которых градиент этой функции равен нулю:
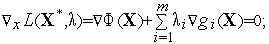
(4)
Находим точки, в которых нарушаются условия регулярности ограничивающих функций.
Во всех стационарных точках функции, а также точках нарушенияусловий регулярности ограничивающих функцийвычисляем значения функции
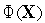 и
выбираем ту (или те), в которой значение
функции наименьшее
и
выбираем ту (или те), в которой значение
функции наименьшее
Аналитическое решение задачи НП. Тест 1
Пусть дана двумерная задача нелинейного программирования с ограничениями типа неравенств
|
|
(1) |
где
![]() ,
,
|
|
(2) |
1. Дайте определение задачи нелинейного программирования(1), (2).
2. Изобразите на рисунке область допустимых значений вектора варьируемых параметров, формируемую ограничениями (2).
3. Найдите аналитически решение этой задачи без использования теоремы Куна-Таккераи изобразите его на рисунке.
Ответ
1.
Задача (1), (2) является задачей
выпуклого программирования: множество
![]() есть
выпуклый многогранник, а функция
есть
выпуклый многогранник, а функция
![]() (
(![]() )
- квадратичная.
)
- квадратичная.
2. Область допустимых значений вектора варьируемых параметров, формируемая ограничениями (2), имеет вид, представленный на рис. 1.
|
|
Рис. 1.
3. Аналитическое решение задачи нелинейного программирования (1), (2) без использования теоремы Куна-Таккерасостоит из следующих шагов.
Определяем стационарные точки функции
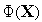 в
области
в
области
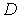 .
.
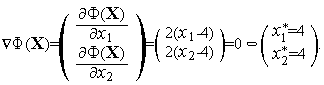 Обозначим
Обозначим
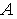 найденную
стационарную
точку функции
найденную
стационарную
точку функции
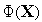 .
Легко видеть (см. рис. 1), что точка
.
Легко видеть (см. рис. 1), что точка
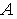 не
принадлежит множеству
не
принадлежит множеству
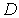 и
должна быть исключена из дальнейшего
рассмотрения.
и
должна быть исключена из дальнейшего
рассмотрения.Определяем критические точки функции
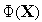 в
области
в
области
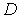 .
.
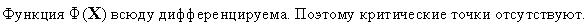
Для каждой из границ области
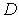 решаем
соответствующую задачу на условный
минимум:
решаем
соответствующую задачу на условный
минимум:
Граница
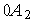 .
Решаем задачу
.
Решаем задачу
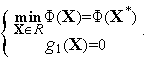 Из
условия
Из
условия
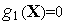 имеем
имеем
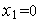 .
Подставив это значение
.
Подставив это значение
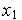 в
выражение для
в
выражение для
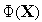 ,
получим
,
получим
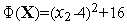 .
Минимум этой функции достигается в
точке
.
Минимум этой функции достигается в
точке
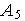 с
координатами
с
координатами
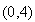 :
: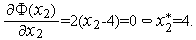
Граница
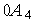 .
Решаем задачу
.
Решаем задачу
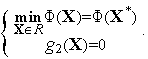 Аналогично
предыдущему имеем точку
Аналогично
предыдущему имеем точку
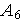 с
координатами
с
координатами
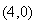 .
.Граница
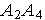 .
Решаем задачу
.
Решаем задачу
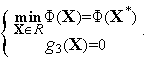 Из
условия
Из
условия
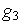 (
(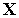 )=0
имеем
)=0
имеем
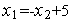 .
Подставив это значение
.
Подставив это значение
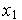 в
выражение для функции
в
выражение для функции
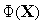 ,
получим
,
получим
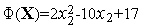 .
Минимум этой функции достигается в
точке
.
Минимум этой функции достигается в
точке
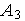 с
координатами
с
координатами
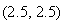 :
:
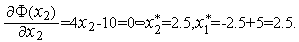
Пересечением
границ области
![]() являются
точки
являются
точки
![]()
Значения
функции
![]() в
отобранных точках приведены в табл. 1.
в
отобранных точках приведены в табл. 1.
Таблица 1
|
Точка |
|
|
|
|
|
|
|
Координаты |
(0,0) |
(0,5) |
(2.5,2.5) |
(5,0) |
(0,4) |
(4,0) |
|
Значение
|
32 |
17 |
4.5 |
17 |
16 |
16 |
Из
табл. 1 следует, что искомое минимальное
значение
![]() достигается
в точке
достигается
в точке
![]() и
равно
и
равно
![]() .
.
Аналитическое решение задачи НП. Тест 2
Пусть дана двумерная задача нелинейного программирования с ограничениями типа неравенств
|
|
(1) |
где
![]() ,
,
|
|
(2) |
1. Изобразите на рисунке область допустимых значений вектора варьируемых параметров, формируемую ограничениями (2).
2. Найдите аналитически решение этой задачи с использованием теоремы Куна-Таккераи изобразите его на рисунке.
Ответ
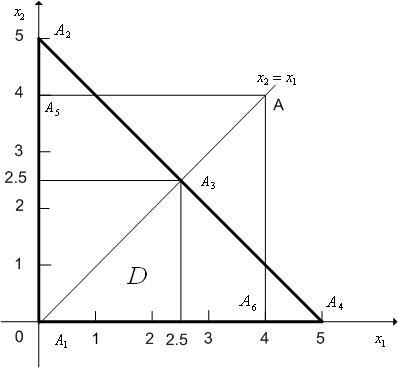
1. Область допустимых значений вектора варьируемых параметров, формируемая ограничениями (2), имеет вид, представленный на рис. 1.
|
|
Рис. 1.
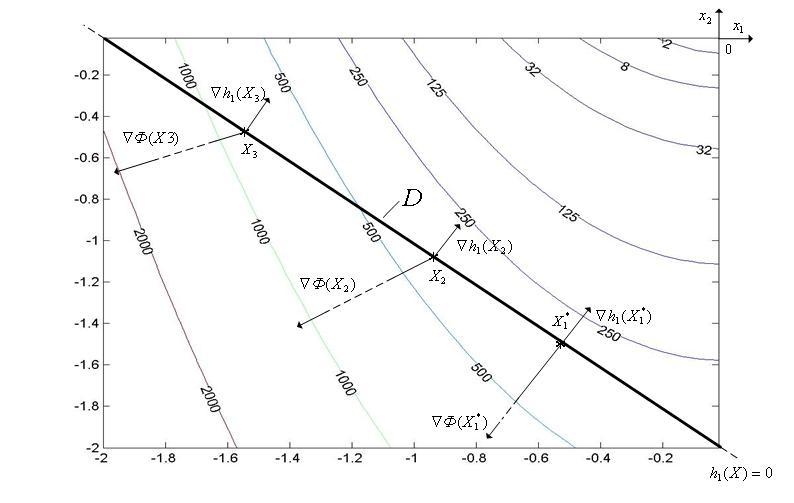
2. Аналитическое решение задачи нелинейного программирования(1),(2) с использованиемтеоремы Куна-Таккерасостоит из следующих шагов.
Записываем функцию Лагранжа
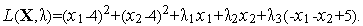
Находим градиенты функций
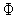 (
(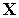 ),
),
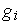 (
(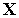 ),
),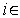 [1,3]:
[1,3]:
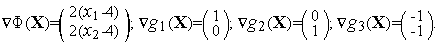
Записываем необходимое условие минимума функции Лагранжа:
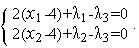
(3)
а). Положим, что ни одно из ограничений не является активным ограничением(точка лежит внутри области
 ).
В этом случае можно положить
).
В этом случае можно положить
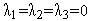 (напомним,
что теорема
Куна-Таккеране запрещает этого).
Тогда из (3) имеемстационарную
точку функции
(напомним,
что теорема
Куна-Таккеране запрещает этого).
Тогда из (3) имеемстационарную
точку функции
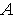 с
координатами
с
координатами
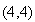 .
Точка лежит вне области
.
Точка лежит вне области
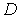 и
из рассмотрения исключается.
и
из рассмотрения исключается. б). Пусть активным является ограничение
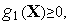 т.е.
пусть
т.е.
пусть
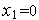 .
Тогда можно положить
.
Тогда можно положить
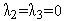 .
При этом из (9) следует
.
При этом из (9) следует
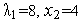 .
Таким образом, имеем стационарную
точку функции
.
Таким образом, имеем стационарную
точку функции
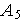 с
координатами
с
координатами
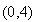 .
.в). Пусть активным является ограничение
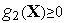 ,
т.е. пусть
,
т.е. пусть
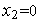 .
Тогда можно положить
.
Тогда можно положить
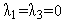 .
При этом из (3) следует
.
При этом из (3) следует
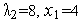 .
Таким образом, имеем стационарную
точку функции
.
Таким образом, имеем стационарную
точку функции
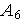 с
координатами
с
координатами
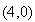 .
.г). Пусть активным является ограничение
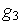 (
(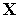 )
)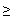 0,
т.е. пусть
0,
т.е. пусть
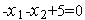 .
Тогда можно положить
.
Тогда можно положить
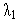 =
=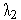 =0.
При этом из (3) следует система
=0.
При этом из (3) следует система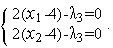
(4)
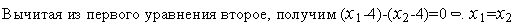

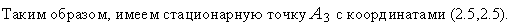
д) Пусть активными являются ограничения
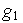 (
(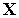 )
)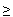 0,
0,
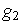 (
(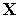 )
)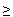 0,
т.е. пусть
0,
т.е. пусть
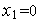 ,
,
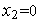 .
Тогда можно положить
.
Тогда можно положить
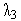 =0.
При этом из (3) следует
=0.
При этом из (3) следует
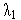 =8,
=8,
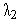 =8.
Таким образом, имеем стационарную
точку функции
=8.
Таким образом, имеем стационарную
точку функции
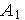 с
координатами
с
координатами
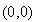 .
.е) Аналогично получаем стационарную точку
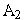 с
координатами
с
координатами
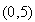 .
.ж) Аналогично получаем стационарную точку
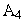 с
координатами
с
координатами
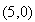 .
.
Легко видеть, что точки, в которых нарушаются условия регулярности ограничивающих функций, отсутствуют.
Значения
функции
![]() (
(![]() )
в отобранных точках приведены в табл. 1.
)
в отобранных точках приведены в табл. 1.
Таблица 1
|
Точка |
|
|
|
|
|
|
|
Координаты |
(0,0) |
(0,5) |
(2.5,2.5) |
(5,0) |
(0,4) |
(4,0) |
|
Значение
|
32 |
17 |
4.5 |
17 |
16 |
16 |
Из
табл. 1 следует, что искомое минимальное
значение
![]() достигается
в точке
достигается
в точке
![]() и
равно 4.5.
и
равно 4.5.