- •Глава 1. Математическая формулировка задачи непрерывной оптимизации в конечномерном пространстве
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения
- •Глава 12. Задачи оптимального управления и методы их приближенного решения
- •Глава 1. Математическая формулировка задачи оптимального проектирования.
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации.
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения.
- •Глава 4. Методы поиска локального минимума одномерных функций.
- •Глава 5. Методы поиска глобального минимума одномерных функций.
- •Глава 6. Многомерная локальная безусловная оптимизация. Детерминированные прямые методы.
- •Глава 7. Многомерная локальная безусловная оптимизация. Детерминированные методы первого и второго порядков.
- •1. Постановка задачи.
- •2. Итерационная формула.
- •Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска (прямые методы).
- •Глава 9. Многомерная локальная условная оптимизация.
- •Глава 10. Многомерная глобальная условная оптимизация.
- •Глава 11. Задачи многокритериальной оптимизации и методы их решения.
- •Глава 12. Задачи оптимального управления и методы их приближенного решения.
Глава 3. Классификация поисковых методов оптимизации и методология их сравнения.
3.1 Классификация методов решения детерминированных задач оптимизации
Особенность
задач оптимизации в САПР состоит в том,
что вычисление значения критерия
оптимальностии значенийограничивающих
функцийпри фиксированных значениях
параметров
![]() может
требовать больших затрат компьютерного
времени. В связи с этим возникает проблема
решения задачи оптимизации при наименьшем
числе испытаний.
может
требовать больших затрат компьютерного
времени. В связи с этим возникает проблема
решения задачи оптимизации при наименьшем
числе испытаний.
Рассмотрим для простоты записи только ограничении типа неравенств:
![]()
Испытаниемназывается операция однократного
вычисления функций
![]()
![]() и,
быть может, их производных, в некоторой
точке
и,
быть может, их производных, в некоторой
точке
![]() .
.
Далее
будем говорить, что детерминированная
задача оптимизациирешается с помощьюпоискового
метода оптимизации, если используется
следующая процедура поиска оптимального
решения
![]() :
:
по очереди при
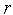 =0,1,2,…,
=0,1,2,…,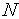 -1
производятся испытанияв точках
-1
производятся испытанияв точках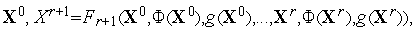
(1)
где
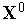 —
начальное приближение;
—
начальное приближение;в качестве решения задачи берется вектор
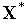 ,
который находится из условия
,
который находится из условия
-
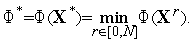
(2)
Классификация по наличию или отсутствию ограничений на вектор варьируемых параметров.
Метод поиска, ориентированный на решение задач безусловной оптимизации, называетсяметодом безусловной оптимизации. Аналогично, метод поиска, ориентированный на решениезадач условной оптимизации, называетсяметодом условной оптимизации.
Классификация по размерности вектора X.
Если
в формулах (1), (2)
![]() есть
скаляр, то метод поиска называется
одномерным
методом поиска; если
есть
скаляр, то метод поиска называется
одномерным
методом поиска; если
![]() есть
вектор (
есть
вектор (![]() >1),
то метод поиска называется
многопараметрическим
методом поиска.
>1),
то метод поиска называется
многопараметрическим
методом поиска.
Классификация по характеру искомого решения.
Если
метод поиска гарантирует отыскание
только локального минимума функции
![]() (
(![]() ),
то метод называется методом
локального поиска. Если делается
попытка отыскать глобальный минимум
),
то метод называется методом
локального поиска. Если делается
попытка отыскать глобальный минимум
![]() (
(![]() ),
то метод называется методом
глобального поиска. Сразу отметим,
что удовлетворительных с точки зрения
вычислительной эффективности методов
глобального поиска не существует.
),
то метод называется методом
глобального поиска. Сразу отметим,
что удовлетворительных с точки зрения
вычислительной эффективности методов
глобального поиска не существует.
Классификация по характеру функции Fr.
Если
функции
![]() ,
,
![]() являются
детерминированными, то метод поиска
называется детерминированным
методом поиска. Если функции
являются
детерминированными, то метод поиска
называется детерминированным
методом поиска. Если функции
![]() содержат
случайные параметры, то метод поиска
называется стохастическим
методом поиска.
содержат
случайные параметры, то метод поиска
называется стохастическим
методом поиска.
Методы пассивного и последовательного поиска.
Если
все точки
![]() ,
,
![]() =0,1,2,…,
=0,1,2,…,![]() назначаются заранее (до проведения
испытаний),
то метод поиска называетсяпассивным
методом поиска. Если точка
назначаются заранее (до проведения
испытаний),
то метод поиска называетсяпассивным
методом поиска. Если точка
![]() определяется
на основе всей или части информации об
испытаниях в предыдущих точках, то метод
называется последовательным
методом поиска.
определяется
на основе всей или части информации об
испытаниях в предыдущих точках, то метод
называется последовательным
методом поиска.
Классификация по количеству предыдущих учитываемых шагов.
Если
при вычислении координат точки
![]() учитывается
информация только об одном (предыдущем)
испытании,
то метод поиска называетсяодношаговым
методом поиска.
учитывается
информация только об одном (предыдущем)
испытании,
то метод поиска называетсяодношаговым
методом поиска.
Схема
одношагового последовательного
метода поиска:![]()
Если
при вычислении координат точки
![]() учитывается
информация о
учитывается
информация о
![]() >1
предыдущих испытаниях,
то метод поиска называетсямногошаговым
методом поиска(конкретнее,
>1
предыдущих испытаниях,
то метод поиска называетсямногошаговым
методом поиска(конкретнее,
![]() -шаговым).
-шаговым).
Классификация по виду функций Fr.
Если
функции
![]() на
всех
на
всех
![]() шагах
одинаковы, то метод поиска называется
итерационным
методом поиска.
шагах
одинаковы, то метод поиска называется
итерационным
методом поиска.
Схема
одношагового итерационного метода
последовательного поиска:
![]()
Если
функции
![]() различны
на различных шагах поиска, то метод
называется не
итерационным методом поиска.
различны
на различных шагах поиска, то метод
называется не
итерационным методом поиска.
Классификация по "близости" точек соседних точек, в которых производятся испытания.
Если
точка
![]() принадлежит
некоторой малой окрестности точки
принадлежит
некоторой малой окрестности точки
![]() ,
т.е.
,
т.е.
![]() ,
то метод поиска называется локальным
методом поиска. Если точка
,
то метод поиска называется локальным
методом поиска. Если точка
![]() может
принадлежать любой точки множества
может
принадлежать любой точки множества
![]() ,
т.е.
,
т.е.
![]() ,
то метод поиска называется нелокальным
методом поиска.
,
то метод поиска называется нелокальным
методом поиска.
Классификация по порядку используемых производных.
Если
при вычислении значений функции
![]() производные
не используются, то метод поиска
называется прямым
методом поискаилиметодом
поиска нулевого порядка. Если при
этом используются производные
производные
не используются, то метод поиска
называется прямым
методом поискаилиметодом
поиска нулевого порядка. Если при
этом используются производные
![]() -го
порядка, то метод поиска называется
методом
поиска k-го порядка. Метод поиска
первого порядка называется такжеградиентным
методом поиска.
-го
порядка, то метод поиска называется
методом
поиска k-го порядка. Метод поиска
первого порядка называется такжеградиентным
методом поиска.
Способ
выбора начальной точки
![]() и
конкретная совокупность функций
и
конкретная совокупность функций
![]() называются
алгоритмом
поисковой оптимизации. Таким образом,
понятие алгоритма является более частным
по сравнению с понятием метода (одному
и тому же методу могут соответствовать
различные алгоритмы).
называются
алгоритмом
поисковой оптимизации. Таким образом,
понятие алгоритма является более частным
по сравнению с понятием метода (одному
и тому же методу могут соответствовать
различные алгоритмы).
Важной проблемой при построении методов решения задач оптимизации является проблема выбора условия окончания поиска (критерия окончания поиска). Простейшими, но широко используемыми в вычислительной практике, являются следующие критерии окончания поиска:
|
|
(3) |
где
![]() —
константа, определяющая требуемую
точность решения по
—
константа, определяющая требуемую
точность решения по
![]() ;
;
|
|
(4) |
где
![]() —
константа, определяющая требуемую
точность решения по
—
константа, определяющая требуемую
точность решения по
![]() .
Здесь
.
Здесь
![]() —
некоторая векторная норма (например,
евклидова).
—
некоторая векторная норма (например,
евклидова).
Будем далее условия окончания поиска (3), (4) называть стандартными условиями окончания поиска(стандартными критериями окончания поиска).
Итерационная формула метода решения детерминированной задачи НП. Тест 1
Пусть итерационная формула некоторого метода решения детерминированных задач оптимизацииимеет следующий вид:
![]() =
=![]() (
(![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),
![]() ,
,![]() (
(![]() ),g(
),g(![]() )).
Дайте определение этого метода.
)).
Дайте определение этого метода.
Ответ
Итерационная
формула
![]() =
=![]() (
(![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),
![]() ,
,![]() (
(![]() ),g(
),g(![]() ))
определяет двухшаговый итерационный
метод последовательного поиска.
))
определяет двухшаговый итерационный
метод последовательного поиска.
Итерационная формула метода решения детерминированной задачи НП. Тест 2
Запишите общий вид итерационной формулы для трехшагового итерационного метода последовательного поиска решения детерминированных задач оптимизации.
Ответ
В общем случае итерационная формула для трехшагового итерационного метода последовательного поиска имеет следующий вид:
![]() =
=![]() (
(![]() ,
,![]() (
(![]() ),
),![]() (
(![]() ),
),
![]() ,
,![]() (
(![]() ),g(
),g(![]() )
)
![]() ,
,![]() (
(![]() ),g(
),g(![]() )).
)).
3.2 Наилучшие алгоритмы оптимизации
Конкретную детерминированную задачу оптимизацииможно решить различными алгоритмами. Отсюда возникают вопросы:
какой алгоритм выбрать?
какой алгоритм является «наилучшим»?
Ответ
на эти вопросы возможен только в том
случае, когда определен класс функций
![]() ,
которому принадлежит критерий
оптимальности
,
которому принадлежит критерий
оптимальности
![]() .
Без определения этого класса ответить
на поставленные вопросы невозможно –
нет алгоритма, наилучшего для всех
возможных функций
.
Без определения этого класса ответить
на поставленные вопросы невозможно –
нет алгоритма, наилучшего для всех
возможных функций
![]()
Примеры классов функций:
класс функций с ограниченным числом минимумов;
класс функций, с ограниченными некоторой величиной первыми частными производными;
класс выпуклых функций.
Множество
рассматриваемых алгоритмов оптимизации
обозначим {![]() }.
}.
Для
формальной постановки задачи определения
наилучшего алгоритма из множества
![]() на
классе функций
на
классе функций
![]() необходимо
еще ввести критерий
качества алгоритма оптимизации.
Обозначим этот критерий
необходимо
еще ввести критерий
качества алгоритма оптимизации.
Обозначим этот критерий
![]() ,
где
,
где
![]() ,
,
![]() .
Положим, что оптимальным является
наименьшее значение этого критерия.
.
Положим, что оптимальным является
наименьшее значение этого критерия.
Для
построения критерия качества алгоритма
на всем классе функций
![]() можно
воспользоваться
можно
воспользоваться
принципом гарантированного результата:
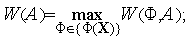
некоторым средним значением критерия качества алгоритма на классе функций
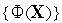 .
.
Если
критерий качества алгоритма на классе
функций
![]() тем
или иным образом определен, то задача
отыскания наилучшего
алгоритма оптимизациина этом классе
функций формально может быть записана
в следующем виде:
тем
или иным образом определен, то задача
отыскания наилучшего
алгоритма оптимизациина этом классе
функций формально может быть записана
в следующем виде:
|
|
(1) |
Теоретическое решение задачи (1) возможно только для алгоритмов поиска минимума одномерных унимодальных функций. В более сложных случаях сравнениеалгоритмов поисковой оптимизациии выбор из них наилучшего производится на основе экспериментального тестирования.
3.3 Экспериментальное тестирование алгоритмов оптимизации
В
качестве критерия
качества алгоритма оптимизации
![]() обычно
рассматривают затраты времени на поиск.
Эти затраты складываются
обычно
рассматривают затраты времени на поиск.
Эти затраты складываются
из затрат на испытания
из затрат на нахождение точек
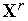 по
информации о предыдущих испытаниях(можно сказать – из затрат на вычисления
значений функции
по
информации о предыдущих испытаниях(можно сказать – из затрат на вычисления
значений функции
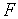 ).
).
Поскольку
в задачах САПР последние затраты много
меньше первых, в качестве критерия
качества алгоритма оптимизацииA
можно использовать количествоиспытаний
![]() ,
необходимых для нахождения минимума
функции
,
необходимых для нахождения минимума
функции
![]() с
заданной точностью
с
заданной точностью
![]() при
начальном приближении
при
начальном приближении
![]() .
.
Для
корректного сравнения эффективности
различных алгоритмов, экспериментальное
тестирование алгоритмов оптимизациинеобходимо выполнять при одинаковых
значениях заданной точности решения
![]() .
Поэтому будем в качестве критерия
качества алгоритма оптимизации
.
Поэтому будем в качестве критерия
качества алгоритма оптимизации
![]() на
классе функций {
на
классе функций {![]() (
(![]() )}
использовать критерий
)}
использовать критерий
![]() .
.
При
заданной точности решения эффективность
любого алгоритма
поисковой оптимизациизависит от
начального приближения
![]() .
Поэтому при экспериментальном тестировании
обычно критерий
.
Поэтому при экспериментальном тестировании
обычно критерий
![]() усредняют
по множеству
допустимых значений вектора варьируемых
параметров
усредняют
по множеству
допустимых значений вектора варьируемых
параметров
![]() .
Обозначим такой критерий
.
Обозначим такой критерий
![]() .
.
Точность
решения задачи оптимизации определяется
используемым условием окончания поиска.
При экспериментальном тестировании в
качестве такого условия обычно используют
одно из двух следующих условий:
![]()
где
![]() -
значение функции
-
значение функции
![]() (
(![]() )
в точке истинного минимума;
)
в точке истинного минимума;
![]()
где
![]() -
точка истинного минимума функции
-
точка истинного минимума функции
![]() (
(![]() ),
),
![]() *
*![]() - некоторая векторная норма.
- некоторая векторная норма.
Заметим,
что эти условия накладывают на класс
тестовых функций дополнительное
требование: у этих функций априори
должно быть известно положение истинного
минимума
![]() .
.
Первоначально
в качестве тестовых функций использовали
одну или несколько наиболее «трудных»
тестовых функций (многоэкстремальных,
овражных и т.п.). В настоящее время для
оценки качества алгоритмов
поисковой оптимизацииобычно используют
среднее значение критерия
![]() на
классе функций
на
классе функций
![]() .
Обозначим такой критерий через
.
Обозначим такой критерий через![]() .
.
Тогда формально задачу поиска наилучшего алгоритма оптимизацииможно записать в следующем виде:
|
|
(1) |
Особенности задачи (1):
высокая дисперсия оценки
 ;
;функция
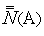 может
оказаться многоэкстремальной;
может
оказаться многоэкстремальной;может оказаться, что при некоторых
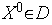 решение
задачи минимизации затягивается сверх
допустимого времени.
решение
задачи минимизации затягивается сверх
допустимого времени.
Последняя
особенность приводит к тому, что кроме
критерия
![]() приходится
использовать еще вероятность локализации
минимума функции
приходится
использовать еще вероятность локализации
минимума функции
![]() за
допустимое количество испытаний
за
допустимое количество испытаний
![]() .
Таким образом, вообще говоря, задача
экспериментального тестирования
является задачей
многокритериальной оптимизации(точнее, задачей двухкритериальной
оптимизации).
.
Таким образом, вообще говоря, задача
экспериментального тестирования
является задачей
многокритериальной оптимизации(точнее, задачей двухкритериальной
оптимизации).
Сделаем следующие предположения:
множество тестируемых алгоритмов {
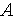 }
состоит из
}
состоит из
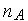 алгоритмов
алгоритмов
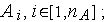
при тестировании алгоритма
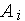 ,
,
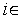 [1,
[1,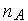 ]
используется совокупность
]
используется совокупность
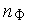 тестовых
функций
тестовых
функций
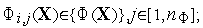
при тестировании алгоритма
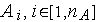 с
помощью функции
с
помощью функции
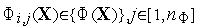 используется
используется
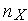 начальных
приближений вектора
варьируемых параметров
начальных
приближений вектора
варьируемых параметров
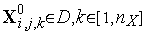 .
.
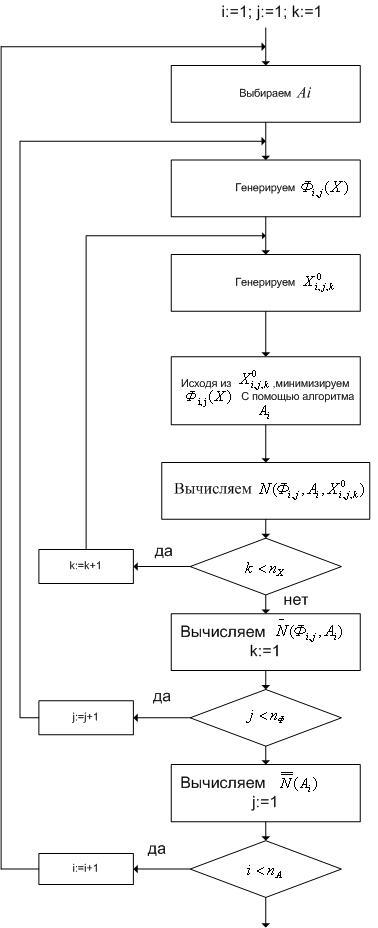
В сделанных предположениях общую схему экспериментального тестирования алгоритмов оптимизацииможно представить в следующем виде (см. рис. 1).
|
|
Рис. 1. Общая схема экспериментального тестирования алгоритмов поисковой оптимизации.
Заметим,
что для получения статистически
достоверных оценок значений
![]() ,
,
![]() ,
величины
,
величины
![]() ,
,
![]() должны
быть достаточно велики.
должны
быть достаточно велики.
3.4 Классы тестовых функций
Класс одномерных унимодальных функций.
Положим,
что
![]() .
Покроем интервал
.
Покроем интервал
![]() сеткой
с
сеткой
с
![]() узлам
и обозначим
узлам
и обозначим
![]() .
.
Положим,
что необходимо построить одномерную
унимодальную функцию, минимум которой
находится в узле
![]() ,
т.е. в точке
,
т.е. в точке
![]() .Тогда
для генерации такой функций может быть
использован следующий алгоритм построения
тестовых одномерных унимодальных
функций.
.Тогда
для генерации такой функций может быть
использован следующий алгоритм построения
тестовых одномерных унимодальных
функций.
Генерируем дискретную случайную величину
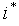 ,
равномерно распределенную на множестве
0,1,2,…,
,
равномерно распределенную на множестве
0,1,2,…,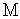 .
.
Генерируем случайные числа
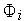 по
рекуррентной формуле
по
рекуррентной формуле
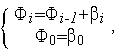 где
где
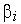 ,
,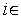 [0,
[0,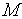 ]
- случайные величины, равномерно
распределенные в интервале
]
- случайные величины, равномерно
распределенные в интервале
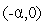 ,
если
,
если
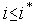 ,
и в интервале (
,
и в интервале (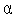 ,0),
если
,0),
если
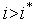 .
Здесь
.
Здесь
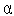 -
некоторая константа, определяющая
максимальную скорость изменения искомой
функции.
-
некоторая константа, определяющая
максимальную скорость изменения искомой
функции.Для получения функции
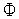 (
(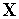 )
используем линейную интерполяцию
полученных значений
)
используем линейную интерполяцию
полученных значений
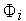 ,
,
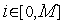 .
Минимум полученной функции
.
Минимум полученной функции
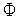 (
(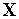 )
достигается в точке
)
достигается в точке
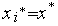 .
.
Класс одномерных многоэкстремальных функций.
Положим,
то область допустимых значений
![]() есть
интервал [
есть
интервал [![]() ,
,![]() ].
С помощью линейного преобразования
].
С помощью линейного преобразования
![]()
сведем
этот интервал к интервалу [0,1]. Тогда в
качестве тестовых одномерных
многоэкстремальных функций можно
использовать тригонометрические
полиномы некоторой степени
![]() (отрезки
ряда Фурье):
(отрезки
ряда Фурье):
|
|
(1) |
Здесь
![]() ,
,
![]() ,
,
![]() ,
,
![]() =[1,
=[1,![]() ]
случайные величины с некоторыми законами
распределения.
]
случайные величины с некоторыми законами
распределения.
Таким образом, алгоритм генерации тестовых одномерных многоэкстремальных функцийсостоит в генерации указанных случайных величин и использовании формулы (1).
Класс многоэкстремальных функций нескольких переменных.
В простейшем случае алгоритм генерации многоэкстремальных функций нескольких переменныхможно построить на основе использования совокупности s квадратичных функций, каждая из которых в общем случае дает локальный минимум искомой функции:
|
|
(2) |
где квадратичная функция
|
|
(3) |
Здесь
![]() –
размерность вектора
варьируемых параметров
–
размерность вектора
варьируемых параметров
![]() ,
,
![]() –
точка
–
точка
![]() -го
локального минимума глубиной
-го
локального минимума глубиной
![]() ;
постоянные
;
постоянные
![]() ,
,
![]() ,
,
![]() -
случайные величины с некоторыми законами
распределения.
-
случайные величины с некоторыми законами
распределения.
Генерация тестовых функций. Тест 1
Пусть
![]() =[0,1],
=[0,1],
![]() =1,
=1,
![]() =10
и пусть имеются следующие значения
случайных величин
=10
и пусть имеются следующие значения
случайных величин
![]() :
:
 =4;
=4;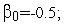
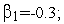
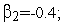
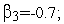
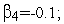
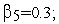

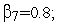

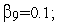
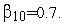
Используя рекуррентную формулу
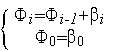
и линейную интерполяцию, изобразить на рисунке график соответствующей одномерной унимодальной функции.
Ответ
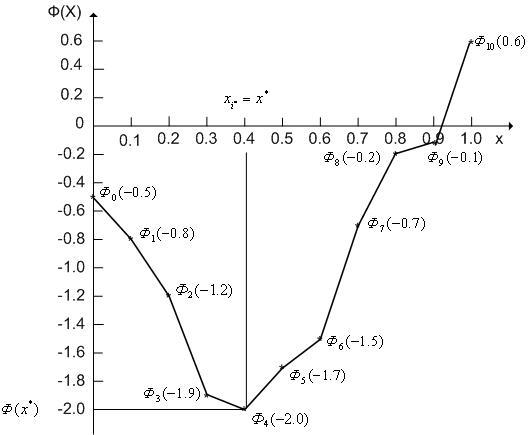
Искомая
одномерная
унимодальная функция
![]() (
(![]() )
имеет вид, представленный на рис. 1.
)
имеет вид, представленный на рис. 1.
|
|
Рис. 1.
Генерация тестовых функций. Тест 2
С
помощью алгоритма
генерации многоэкстремальных функций
нескольких переменныхтребуется на
интервале
![]() выполнить
генерацию трехэкстремальной функции
одной переменной (
выполнить
генерацию трехэкстремальной функции
одной переменной (![]() значениями
величин
значениями
величин
![]() ,
,
![]() ,
,
![]() ,
,
![]() :
:
Таблица 1
|
|
|
|
|
|
1 |
1 |
-6 |
-4 |
|
2 |
1.2 |
0 |
1 |
|
3 |
1.5 |
7 |
7 |
Приведите примерный график этой функции.
Ответ
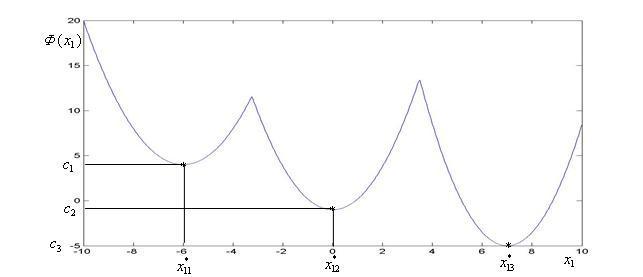
Искомая
функция
![]() (
(![]() )
будут иметь вид, представленный на
рис. 1.
)
будут иметь вид, представленный на
рис. 1.
|
|
Рис. 1.