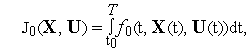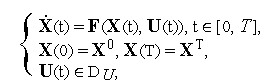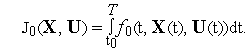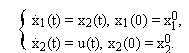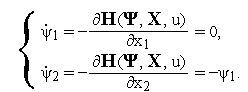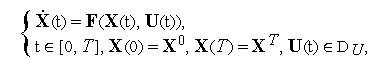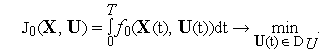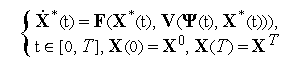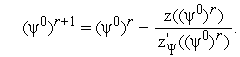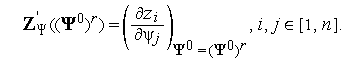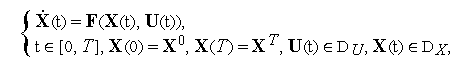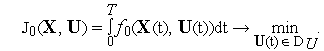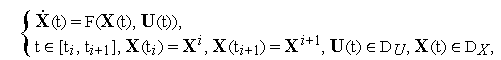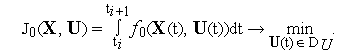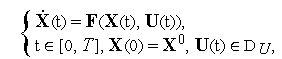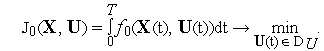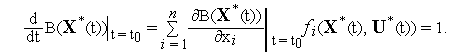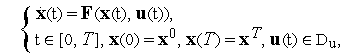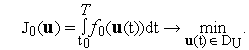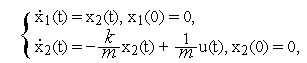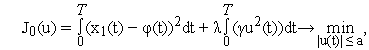- •Глава 1. Математическая формулировка задачи непрерывной оптимизации в конечномерном пространстве
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения
- •Глава 12. Задачи оптимального управления и методы их приближенного решения
- •Глава 1. Математическая формулировка задачи оптимального проектирования.
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации.
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения.
- •Глава 4. Методы поиска локального минимума одномерных функций.
- •Глава 5. Методы поиска глобального минимума одномерных функций.
- •Глава 6. Многомерная локальная безусловная оптимизация. Детерминированные прямые методы.
- •Глава 7. Многомерная локальная безусловная оптимизация. Детерминированные методы первого и второго порядков.
- •1. Постановка задачи.
- •2. Итерационная формула.
- •Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска (прямые методы).
- •Глава 9. Многомерная локальная условная оптимизация.
- •Глава 10. Многомерная глобальная условная оптимизация.
- •Глава 11. Задачи многокритериальной оптимизации и методы их решения.
- •Глава 12. Задачи оптимального управления и методы их приближенного решения.
Глава 12. Задачи оптимального управления и методы их приближенного решения.
12.1 Постановка задачи оптимального управления
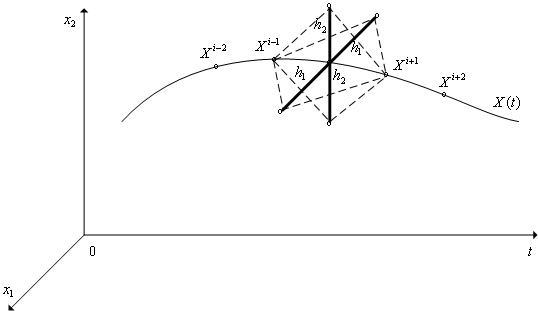
Пусть нестационарная динамическая система описывается системой обыкновенных дифференциальных уравнений (ОДУ)
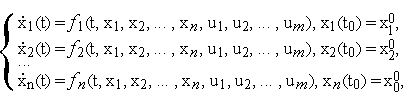
![]()
Здесь
![]() —
—
![]() -вектор
начальных условий,
-вектор
начальных условий,
![]() –
анализируемый период времени (где
величина
–
анализируемый период времени (где
величина
![]() не
обязательно фиксирована!),
не
обязательно фиксирована!),
![]() —
—
![]() -вектор
фазовых переменных системы,
-вектор
фазовых переменных системы,
![]() —
—
![]() —
вектор управления. В той или иной форме
могут быть заданы также условия на конце
траектории системы, например, в виде
—
вектор управления. В той или иной форме
могут быть заданы также условия на конце
траектории системы, например, в виде
![]() .
Заметим, что правильнее было бы последние
условия задавать в виде
.
Заметим, что правильнее было бы последние
условия задавать в виде
![]() ,
где
,
где
![]() —
момент достижения системой состояния
—
момент достижения системой состояния
![]() .
Однако для простоты записи мы будем
использовать первую запись (если не
оговорено противное).
.
Однако для простоты записи мы будем
использовать первую запись (если не
оговорено противное).
Далее будем использовать описание анализируемой динамической системы в векторной форме
|
|
(1) |
Напомним,
что если время
![]() явно
не входит в функцию
явно
не входит в функцию
![]() ,
то динамическая система, описываемая
системой ОДУ (1) называется стационарной.
,
то динамическая система, описываемая
системой ОДУ (1) называется стационарной.
На
вектор
![]() в
общем случае могут быть наложены
ограничения вида
в
общем случае могут быть наложены
ограничения вида
|
|
(2) |
где
![]() –
множество
допустимых значений вектора фазовых
переменных системы,
–
множество
допустимых значений вектора фазовых
переменных системы,
![]() –
некоторое функциональное пространство,
например, пространство
–
некоторое функциональное пространство,
например, пространство
![]() непрерывных
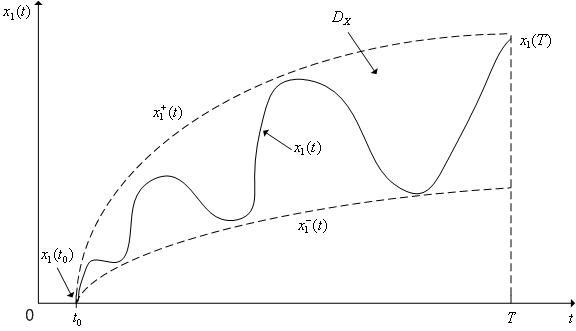
на интервале функций (см. рис. 1).
непрерывных
на интервале функций (см. рис. 1).
На
рис. 1 множество DX
= {x1(t)
| x-1(t)
![]() x1(t)
x1(t)
![]() x+1(t),
t
x+1(t),
t
![]() [t0,
[t0,
![]() ]}
]}
![]() C(0)[t0,
C(0)[t0,
![]() ].
].
|
|
Рис. 1. Пример области допустимых значений вектора фазовых координат для одномерной системы (n = 1).
На
вектор управления
![]() также
обычно накладываются некоторые
ограничения вида
также
обычно накладываются некоторые
ограничения вида
|
|
(3) |
где
![]() –
множество
допустимых управлений,
–
множество
допустимых управлений,
![]() –
некоторое функциональное пространство,
например, пространство
–
некоторое функциональное пространство,
например, пространство
![]() функций
"интегрируемых с квадратом" на
интервале
функций
"интегрируемых с квадратом" на
интервале
![]() (см.
рис. 2).
(см.
рис. 2).
На
рис. 2 множество DU
= {u1(t)
| u-1(t)
![]() u1(t)
u1(t)
![]() u+1(t),
t
u+1(t),
t
![]() [t0,
[t0,
![]() ]}
]}
![]() L2[t0,
L2[t0,
![]() ],
а пространство допустимых управлений
ΩU,
полагается, составляют кусочно-постоянные
функции, имеющие на интервале [t0,
],
а пространство допустимых управлений
ΩU,
полагается, составляют кусочно-постоянные
функции, имеющие на интервале [t0,
![]() ]
конечное число разрывов первого рода.
]
конечное число разрывов первого рода.
|
|
Рис. 2. Пример множества допустимых управлений для системы с одномерным управлением (m = 1).
Примечание 1
Используя
уравнение (1), формально ограничения на
вектор фазовых переменных
![]() можно
пересчитать в ограничения на вектор
управления
можно
пересчитать в ограничения на вектор
управления
![]() .
Однако, задача такого пересчета сложна
и обычно рассматривают и те, и другие
ограничения.
.
Однако, задача такого пересчета сложна
и обычно рассматривают и те, и другие
ограничения.
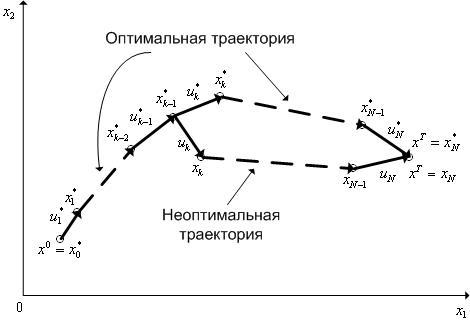
В качестве критерия качества управления(критерий оптимальности управления) взадачах оптимального управленияобычно используют интегральный функционал вида
|
|
(4) |
где
![]() –
некоторая одномерная функция указанных
переменных.
–
некоторая одномерная функция указанных
переменных.
Заметим,
что здесь и далее обозначение функционала
вида
![]() (без
указания зависимости вектор-функций
(без
указания зависимости вектор-функций
![]() от
времени
от
времени
![]() )
означает зависимость
)
означает зависимость
![]() от
этих функций в целом, как элементов
функционального пространства. Часто в
литературе вместо записи
от
этих функций в целом, как элементов
функционального пространства. Часто в
литературе вместо записи
![]() в
том же смысле используют запись
в
том же смысле используют запись
![]() .
.
Итого,
задача
оптимального управления динамической
системойобычно формализуется
следующим образом: найти такой вектор
управления
![]() ,
удовлетворяющий условию (3), который на
решениях системы ОДУ (1) обеспечивает
минимум критерия оптимальности (4) при
выполнении ограничений (2) на вектор
фазовых переменных
,
удовлетворяющий условию (3), который на
решениях системы ОДУ (1) обеспечивает
минимум критерия оптимальности (4) при
выполнении ограничений (2) на вектор
фазовых переменных
![]() .
.
Заметим, что возможны и не интегральные формы функционалов качества управления, например:
![]() ,
где
,
где
![]() –
заданная точка;
–
заданная точка;
![]()
Важным
частным случаем задачи
оптимального управленияявляетсязадача
оптимального быстродействия.Критерий
оптимальности управленияполучается
в этом случае из критерия оптимальности
(4) при
![]() и
имеет вид
и
имеет вид
Постановка задачи оптимального управления. Тест 1
Тело
массой
![]() ,
находящееся в начальный момент времени
,
находящееся в начальный момент времени
![]() в
состоянии покоя в точке с координатой
в
состоянии покоя в точке с координатой
![]() ,
может перемещаться вдоль оси
,
может перемещаться вдоль оси
![]() под
действием силы тяги двигателя, которым
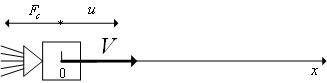
оно снабжено (см. рис. 1).
под
действием силы тяги двигателя, которым
оно снабжено (см. рис. 1).
Максимальная
по величине сила тяги
![]() ,
которую может развить двигатель, равна
,
которую может развить двигатель, равна
![]() .
.
При
движении тела на него действует сила
сопротивления среды
![]() ,
пропорциональная скорости движения
тела
,
пропорциональная скорости движения
тела
![]() ,
т.е.
,
т.е.
![]() ,
где
,
где
![]() –
заданный коэффициент пропорциональности.
–
заданный коэффициент пропорциональности.
Расход
горючего при работе двигателя
пропорционален квадрату развиваемой
им силы тяги, т.е. равен
![]() ,
где
,
где
![]() —
заданная константа.
—
заданная константа.
Необходимо
управлять работой двигателя на промежутке
времени
![]() таким
образом, чтобы при минимальном расходе
горючего закон движения тела (т.е.
зависимость
таким
образом, чтобы при минимальном расходе
горючего закон движения тела (т.е.
зависимость
![]() )
как можно меньше отличался от требуемого
закона движения
)
как можно меньше отличался от требуемого
закона движения
![]() .
.
|
|
Рис. 1.
Формализуйте поставленную задачу в виде задачи оптимального управления динамической системой.
Ответ
Введем обозначения
![]()
Таким
образом, размерность вектора фазовых
переменных системы равна
![]() и
его можно записать в виде
и
его можно записать в виде
![]() .
.
По второму закону Ньютона имеем
![]()
где
![]() –
ускорение тела.
–
ускорение тела.
Итак,
движение тела на интервале времени
![]() описывает
система обыкновенных дифференциальных
уравнений
описывает
система обыкновенных дифференциальных
уравнений
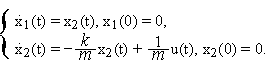
Так
как величина силы тяги в любой момент
времени не может превосходить
![]() ,
имеем ограничение
,
имеем ограничение
![]() .
Т.е. множество
допустимых управленийимеет вид
.
Т.е. множество
допустимых управленийимеет вид
![]()
Ограничения
на вектор фазовых переменных
![]() отсутствуют.
отсутствуют.
Требование
постановки задачи о минимальном отличии
![]() от
от
![]() можно
формализовать различными способами.
Обычно используют метрику функционального
пространства
можно
формализовать различными способами.
Обычно используют метрику функционального
пространства
![]() (гильбертово
пространство)
(гильбертово
пространство)
![]()
Понятно, что минимуму этого функционала соответствует оптимальный случай.
Кроме того, из постановки задачи следует, что необходимо стремиться к минимуму расхода горючего. Для формализации этого требования введем еще один функционал
![]()
Таким образом, в качестве критерия качества управленияможно использовать функционал (двухкритериальная задача!)
![]()
где
![]() –
весовой коэффициент, учитывающий
относительную важность поставленных
целей приближения
–
весовой коэффициент, учитывающий
относительную важность поставленных
целей приближения
![]() к
к
![]() и
экономию горючего
и
экономию горючего
12.2 Принцип максимума Л. С. Понтрягина
Для
простоты записи положим, что
![]() и
рассмотрим стационарную динамическую
систему
и
рассмотрим стационарную динамическую
систему
|
|
(1) |
Требуется
найти управление
![]() ,
которое переводит эту систему из
состояния
,
которое переводит эту систему из
состояния
![]() в
состояние
в
состояние
![]() и
минимизирует критерий
оптимальности управления- функционал
и
минимизирует критерий
оптимальности управления- функционал
|
|
(2) |
Введем
в рассмотрение константу
![]() и
вспомогательную вектор-функцию
и
вспомогательную вектор-функцию
![]() ,
являющуюся решением системы ОДУ
,
являющуюся решением системы ОДУ
![]()
или в векторной форме
![]()
где
|
|
(3) |
гамильтониан
динамической системы (1). Более удобна
другая форма системы обыкновенных
дифференциальных уравнений (ОДУ) для
вспомогательной вектор-функции
![]() :
:
|
|
(4) |
где
![]() -
-
![]() -матрица
частных производных вектор-функции
-матрица
частных производных вектор-функции
![]() по
по
![]() :
:
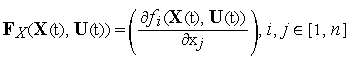
Система ОДУ (4) называется сопряженной системой.
Теорема
1 (принцип
максимума Л.С. Понтрягина). Пусть
![]() –
допустимое управление, переводящее
систему (1) из точки
–
допустимое управление, переводящее
систему (1) из точки
![]() в
точку
в
точку
![]() ,
а
,
а
![]() –
соответствующая фазовая траектория.
Для оптимальности (в смысле минимума
функционала (2)) процесса
–
соответствующая фазовая траектория.
Для оптимальности (в смысле минимума
функционала (2)) процесса
![]() необходимо
существование такой константы
необходимо
существование такой константы
![]() и
такого решения
и
такого решения
![]() системы
ОДУ (5), что вектор- функция
системы
ОДУ (5), что вектор- функция
![]() не
тривиальна и для любого момента времени
не
тривиальна и для любого момента времени
![]() выполняется
условие максимума
выполняется
условие максимума
|
|
(5) |
где
гамильтониан системы
![]() определяется
выражением (4)
определяется
выражением (4)![]()
Не
тривиальность вектор-функции
![]() означает,
что среди величин
означает,
что среди величин
![]() имеется
хотя бы одна тождественно не равная
нулю.
имеется
хотя бы одна тождественно не равная
нулю.
Отметим, что начальные условия для системы ОДУ (5) не заданы, т.е. можно получить только общее решение этой системы.
Примечание 1
Поскольку принцип максимума определяет лишь необходимое условие оптимальности, из того факта, что некоторая траектория удовлетворяет ему, не следует, что она оптимальна. Т.е. принцип максимума дает траектории лишь "подозрительные" на оптимальность. Для определения из их числа оптимальной траектории необходима дополнительная проверка.
Вслед за Федоренко Р.П. назовем систему уравнений (1), (2), (3), (4), (5) П-системой.
Рассмотрим теперь принцип максимума Л.С. Понтрягина для задачи оптимального быстродействия. Напомним, что в этом случаекритерия оптимальности управленияимеет вид (см. параграф 12.1)
|
|
(6) |
Легко видеть, что гамильтониан системы (1) в этом случае равен
|
|
(7) |
Теорема
2 (принцип
максимума Л.С. Понтрягина для задачи
оптимального быстродействия). Пусть
![]() –
допустимое управление, переводящее
систему (1) из точки
–
допустимое управление, переводящее
систему (1) из точки
![]() в
точку
в
точку
![]() ,
а
,
а
![]() –
соответствующая фазовая траектория.
Для оптимальности (в смысле минимума
функционала (6)) процесса
–
соответствующая фазовая траектория.
Для оптимальности (в смысле минимума
функционала (6)) процесса
![]() необходимо
существование такого решения
необходимо
существование такого решения
![]() системы
ОДУ (3), что вектор-функция
системы
ОДУ (3), что вектор-функция
![]() не
тривиальна и для любого момента времени
не
тривиальна и для любого момента времени
![]() и
выполняется условие максимума
и
выполняется условие максимума
|
|
(8) |
где
гамильтониан системы определяется
выражением (7)![]()
Известно множество обобщений принципа максимума Л.С. Понтрягина. Рассмотрим некоторые из них.
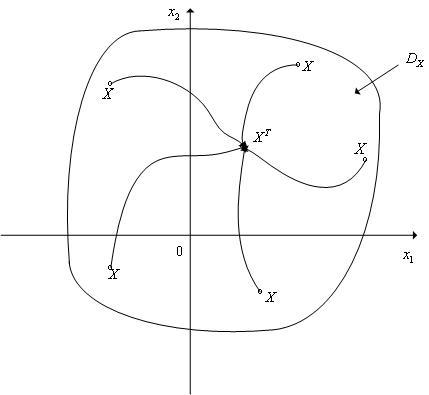
Задача с подвижными концами. Здесь векторы
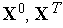 не
фиксированы, а заданы лишь некоторые
гладкие многообразия
не
фиксированы, а заданы лишь некоторые
гладкие многообразия
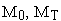 (гладкие
поверхности, расположенные в пространстве
(гладкие
поверхности, расположенные в пространстве
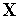 ,
размерность которых меньше
,
размерность которых меньше
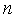 )
такие, что
)
такие, что
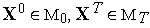 .
.
Дополнительные ограничения на вектор управления. Кроме требования минимизации критерия оптимальности
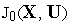 заданы
ограничения вида
заданы
ограничения вида
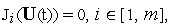 где
где
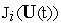 –
некоторые функционалы над
–
некоторые функционалы над
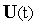 .
.Обобщение для нестационарных динамических систем.
Обобщение для динамических систем с параметрами:
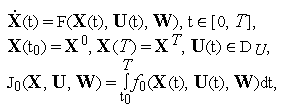 где
где
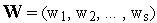 Т
– неизвестный вектор параметров
(констант). Требуется выбрать такой
вектор
Т
– неизвестный вектор параметров
(констант). Требуется выбрать такой
вектор
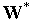 и
такое управление
и
такое управление
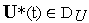 ,
чтобы перевести систему из состояния
,
чтобы перевести систему из состояния
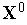 в
состояние
в
состояние
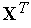 и
минимизировать функционал
и
минимизировать функционал
 .
.
Пример 1
Рассмотрим
материальную точку массой
![]() ,
которая свободно без трения движется
по горизонтальной прямой. Пусть эта
точка снабжена двигателем, развивающим
силу тяги
,
которая свободно без трения движется
по горизонтальной прямой. Пусть эта
точка снабжена двигателем, развивающим
силу тяги
![]() такую,
что
такую,
что
![]() .
.
Введем обозначения
![]()
Таким
образом, для рассматриваемой динамической
системы размерность вектора фазовых
переменных равна
![]() и
этот вектор можно записать в виде
и
этот вектор можно записать в виде
![]() .
.
Аналогично примеру 12.1.1 имеем следующее формальное описание системы (см. рис. 1):
|
|
(9) |
|
|
Рис. 1. К прим. 1.
Поставим
задачу
оптимального быстродействия– задачу
о быстрейшем попадании рассматриваемой
точки в начало координат
![]() из
заданного начального состояния
из
заданного начального состояния
![]() .
Другими словами, поставим задачу перевода
за кратчайшее время материальной точки,
имеющей начальное положение
.
Другими словами, поставим задачу перевода
за кратчайшее время материальной точки,
имеющей начальное положение
![]() и
начальную скорость
и
начальную скорость
![]() ,
в начало координат с нулевой скоростью
(чтобы точка перешла в начало координат
и остановилась там).
,
в начало координат с нулевой скоростью
(чтобы точка перешла в начало координат
и остановилась там).
Гамильтониан (7) системы (9) для задачи оптимального быстродействияимеет вид
![]()
а
система ОДУ для вспомогательной
вектор-функции
![]() —
вид
—
вид
|
|
(10) |
Легко получить явное общее решение системы ОДУ (10)
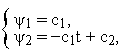
где
![]() —
произвольные постоянные.
—
произвольные постоянные.
Уравнение (8) имеет в данном случае вид
|
|
(11) |
Из
(11) следует, что оптимальное управление
![]() должно
удовлетворять условию
должно
удовлетворять условию
![]()
т.е.
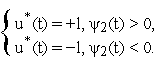
Таким
образом, оптимальное управление
![]() ,
является кусочно-постоянной функцией,
принимающей значения
,
является кусочно-постоянной функцией,
принимающей значения
![]() и
имеющей не более двух интервалов
постоянства (т.к. линейная функция
и
имеющей не более двух интервалов
постоянства (т.к. линейная функция
![]() не
более одного раза меняет знак на отрезке
не
более одного раза меняет знак на отрезке
![]() ).
).
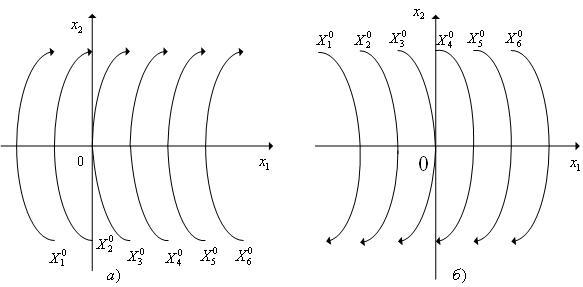
Приведем графическую иллюстрацию полученных результатов.
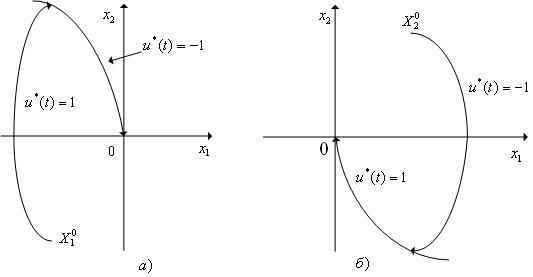
На
отрезке времени, на котором
![]() ,
из (9) последовательно имеем
,
из (9) последовательно имеем
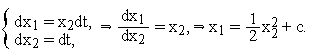
Таким
образом, фазовые траектории, для которых
![]() ,
представляют собой семейство парабол,
соответствующих разным значениям
константы
,
представляют собой семейство парабол,
соответствующих разным значениям
константы
![]() (см.
рис. 2а). По этим параболам фазовые
точки движутся снизу вверх (поскольку
(см.
рис. 2а). По этим параболам фазовые
точки движутся снизу вверх (поскольку
![]() ).
).
Аналогично,
управлению
![]() соответствует
семейство парабол
соответствует
семейство парабол
![]() ,
по которым фазовые точки движутся сверху
вниз (т.к.
,
по которым фазовые точки движутся сверху
вниз (т.к.
![]() )
— см. рис. 2б.
)
— см. рис. 2б.
|
|
Рис. 2. Фазовые траектории системы (9): а – при u*(t)≡1; б – при u*(t)≡-1.
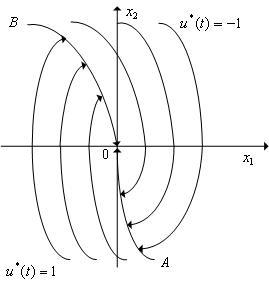
Так
как оптимальное управление
![]() является
кусочно-постоянной функцией, принимающей
значения
является
кусочно-постоянной функцией, принимающей
значения
![]() и
имеющей не более двух интервалов
постоянства, возможны только варианты
оптимальных фазовых траекторий системы,
представленные на рис. 3.
и
имеющей не более двух интервалов
постоянства, возможны только варианты
оптимальных фазовых траекторий системы,
представленные на рис. 3.
|
|
Рис. 3. Варианты фазовых траекторий системы (9).
Т.е. оптимальные фазовые траектории состоят из двух кусков парабол, примыкающих друг к другу. Причем второй из этих кусков лежит на той из парабол, которая проходит через начало координат.
Для произвольных начальных условий имеем следующую картину, представленную на рис. 4.
|
|
Рис. 4. Вид оптимальных фазовых траекторий системы (9).
На
рис. 4 дуга
![]() имеет
уравнение
имеет
уравнение
![]() ,
а дуга
,
а дуга
![]() –
уравнение
–
уравнение
![]() .
.
Итак, согласно принципу максимума Л.С. Понтрягина оптимальные (по быстродействию) фазовые траектории системы (9) могут быть только вида, приведенного на рис. 4.
12.3 Метод решения задачи оптимального управления, использующий П-систему
Рассмотрим задачу оптимального управления
|
|
(1) |
|
|
(2) |
Напомним, что выражения (1), (2) совместно с выражением для соответствующего гамильтониана
|
|
(3) |
сопряженной
системой ОДУ для вспомогательной
вектор-функции
![]()
|
|
(4) |
и условием максимума
|
|
(5) |
образуют П-системузадачи оптимального управления(1), (2).
Наиболее точные и аккуратные методы численного решения задач оптимального управлениясвязаны с решением соответствующихП-систем.
Положим,
что уравнение (5) можно разрешить
относительно
![]() ,
т.е. найти функцию
,
т.е. найти функцию
![]() .
Тогда формально П-система(1), (2), (3), (4) (5) формально сводится к системе
.
Тогда формально П-система(1), (2), (3), (4) (5) формально сводится к системе
![]() уравнений
уравнений
|
|
(6) |
|
|
(7) |
Введем в рассмотрение П-процедуру:
Задаем некоторые начальные условия
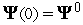 для
функции
для
функции
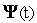 .
.С заданными начальными условиями
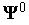 решаем
задачу Коши для сопряженной системы
ОДУ (7) – находим функцию
решаем
задачу Коши для сопряженной системы
ОДУ (7) – находим функцию
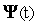 .
.С найденной функцией
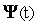 решаем
задачи (6) – отыскиваем оптимальную
фазовую траекторию системы
решаем
задачи (6) – отыскиваем оптимальную
фазовую траекторию системы
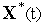 ,
соответствующую начальным условиям
,
соответствующую начальным условиям
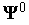 .
.Находим разность
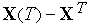 (которая,
очевидно, в общем случае не будет равна
0)
(которая,
очевидно, в общем случае не будет равна
0)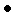
П-процедураустанавливает функциональную зависимость
разности
![]() от
вектора
от
вектора
![]() .
Обозначим эту функциональную зависимость
.
Обозначим эту функциональную зависимость
![]() :
:
|
|
(8) |
|
|
(9) |
Теперь,
формально, решение П-системысводится к решению системы нелинейных
алгебраических уравнений (9): найти
вектор
![]() ,
при котором
,
при котором
![]() или,
что то же самое, при котором
или,
что то же самое, при котором
![]() .
.
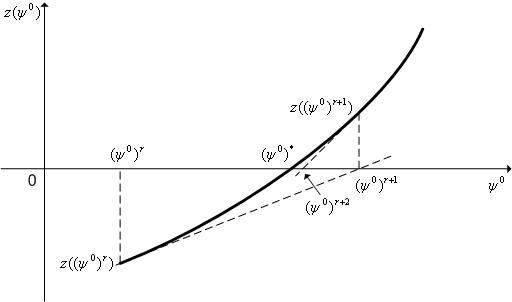
Чаще всего для решения СНАУ (9) используют метод касательных (метод Ньютона). Напомним схему этого метода для одномерного случая (см. параграф 4.8).
Пусть
![]() .
Система (9) при этом имеет вид (см. рис. 1)
.
Система (9) при этом имеет вид (см. рис. 1)
|
|
(10) |
где
![]() —
соответствующие скалярные константы,
а
—
соответствующие скалярные константы,
а
![]() —
скалярные функции.
—
скалярные функции.
|
|
Рис. 1. К схеме метода касательных (метода Ньютона). Одномерный случай (n = 1).
Линейная
функция, аппроксимирующая функцию
![]() в
точке
в
точке
![]() ,
записывается в виде
,
записывается в виде
![]()
Приравняв правую часть этого выражения к нулю, получим итерационную формулу метода касательных
|
|
(11) |
В
многомерном случае
![]() итерационная
формула (11) имеет вид
итерационная
формула (11) имеет вид
|
|
(12) |
где
![]() —
матрица, обратная матрице
—
матрица, обратная матрице
![]() ,
,
|
|
(13) |
Схема метода приближенного решения задачи оптимального управления, использующего П-систему
Полагаем счетчик числа итераций
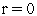 .
.Из каких либо соображений задаем вектор
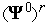 —
начальное значение вектора
—
начальное значение вектора
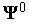 .
.Выполняем П-процедурудля вектора
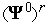 —
вычисляем значение функции
—
вычисляем значение функции
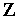 в
точке
в
точке
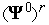 :
:
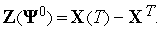
Если условие окончание итераций не выполнено (см. ниже), то по формуле (12) вычисляем следующее приближение к
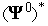 ,
полагаем
,
полагаем
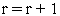 и
переходим к п.3. Иначе переходим к
следующему пункту.
и
переходим к п.3. Иначе переходим к
следующему пункту.В качестве приближения к оптимальному управлению принимаем
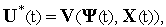 где
где
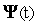 —
решение системы (7) с начальными условиями
—
решение системы (7) с начальными условиями
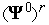
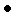
В качестве условия окончания итераций естественно использовать условие
![]()
где
![]() —
некоторая векторная норма, например,
евклидова;
—
некоторая векторная норма, например,
евклидова;
![]() —
требуемая точность выполнения условия
—
требуемая точность выполнения условия
![]() .
.
Рассмотрим в заключение основные трудности, возникающие при решении задачи оптимального управленияданным методом:
Поскольку функция
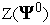 задана
неявно, для вычисления
задана
неявно, для вычисления
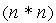 -
матрицы
-
матрицы
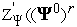 )
приходится использовать численное
дифференцирование. Для этого на каждой
итерации, как минимум, приходится
)
приходится использовать численное
дифференцирование. Для этого на каждой
итерации, как минимум, приходится
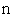 раз
решать задачи Коши (6), (7).
раз
решать задачи Коши (6), (7).Метод Ньютона сходится лишь в достаточно малой окрестности решения. Поэтому на практике приходится использовать различные модификации метода Ньютона, обеспечивающие ускорение сходимости.
Решение уравнения (10) может быть не единственно.
Содержательные соображения для выбора вектора
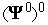 практически
отсутствуют. Иногда для выбора этого
вектора используют приближенное решение
задачи
оптимального управления(1), (2)
каким-либо другим методом, дающим грубое
приближение к
практически
отсутствуют. Иногда для выбора этого
вектора используют приближенное решение
задачи
оптимального управления(1), (2)
каким-либо другим методом, дающим грубое
приближение к
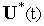 .
.
12.4 Решение задачи оптимального управления методом вариаций в фазовом пространстве
Метод вариаций в фазовом пространстве разработан под руководством Н.Н. Моисеева в ВЦ АН СССР. Имеется несколько вариантов метода. Наиболее развитым является метод локальных вариацийФ.Л. Черноусько.
Рассмотрим задачу оптимального управления
|
|
(1) |
|
|
(2) |
Обратим внимание на то, что в постановке задачи присутствуют кроме ограничений на вектор управления также ограничения на вектор фазовых координат.
Пусть
![]() —
некоторая траектория динамической
системы (1), удовлетворяющая краевым
условиям
—
некоторая траектория динамической
системы (1), удовлетворяющая краевым
условиям
![]() и
фазовым ограничениям
и
фазовым ограничениям
![]() .
Покроем интервал времени
.
Покроем интервал времени
![]() сеткой
с узлами
сеткой
с узлами
![]() и
рассмотрим последовательность точек
и
рассмотрим последовательность точек
![]() ,
которую также будем называть траекторий
системы (1).
,
которую также будем называть траекторий
системы (1).
Элементарной
операциейназывается решение задачи
(1), (2) для интервала
![]() ,
т.е. решение следующей задачи
,
т.е. решение следующей задачи
|
|
(3) |
|
|
(4) |
Обозначим
"цену" элементарной
операции
![]() .
Т.е.
.
Т.е.
![]() —
это значение критерия
качества управления
—
это значение критерия
качества управления
![]() при
оптимальном (в смысле минимума функционала
(4)) переводе системы (1) из состояния
при
оптимальном (в смысле минимума функционала
(4)) переводе системы (1) из состояния
![]() в
состояние
в
состояние
![]() .
.
Заметим,
что в связи с малостью интервала
![]() решать
задачу
оптимального управления(3), (4) не
обязательно очень точно. Это обстоятельство
позволяет во многих случаях достаточно
просто получить ценуэлементарной
операции
решать
задачу
оптимального управления(3), (4) не
обязательно очень точно. Это обстоятельство
позволяет во многих случаях достаточно
просто получить ценуэлементарной
операции
![]() .
.
Во
введенных обозначениях функционал (2)
на траектории
![]() равен
равен
|
|
(5) |
Локальной
вариациейтраектории
![]() (в
фазовом пространстве) называется
траектория, отличающаяся от данной
траектории только значением
(в
фазовом пространстве) называется
траектория, отличающаяся от данной
траектории только значением
![]() в
точке
в
точке
![]() .
Обычно рассматриваются локальные
вариации, в которых точка
.
Обычно рассматриваются локальные
вариации, в которых точка
![]() смещается
только вдоль координатных направлений
(см.рис. 1):
смещается
только вдоль координатных направлений
(см.рис. 1):
![]() .
Здесь
.
Здесь
![]() —
—
![]() -я
компонента вектора
-я
компонента вектора
![]() ,
,
![]() —
—
![]() -й
орт в
-й
орт в
![]() -мерном
пространстве,
-мерном
пространстве,
![]() —
шаг по
—
шаг по
![]() -ой
компоненте фазового вектора.
-ой
компоненте фазового вектора.
|
|
Рис. 1. К определению локальной вариации в фазовом пространстве.
Отметим,
что локальная
вариациятраектории
![]() в
точке
в
точке
![]() приводит
к изменению в сумме (5) только двух
слагаемых —
приводит
к изменению в сумме (5) только двух
слагаемых —
![]() и
и
![]() .
.
Схема метода локальных вариаций.
Из каких либо соображений задаем начальное приближение к оптимальной траектории
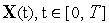 ,
удовлетворяющее краевым условиям
,
удовлетворяющее краевым условиям
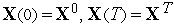 и
фазовым ограничениям
и
фазовым ограничениям
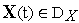 .
Покрываем интервал
.
Покрываем интервал
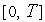 сеткой
с узлами
сеткой
с узлами
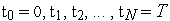 .
Счетчику числа итераций
.
Счетчику числа итераций
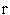 присваиваем
значение
присваиваем
значение
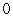 .
.Последовательно для
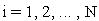 на
интервале
на
интервале
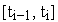 выполняем
элементарную
операциюи определяем ее "цену"
выполняем
элементарную
операциюи определяем ее "цену"
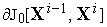 .
.Для каждого
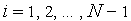 последовательно
для каждого
последовательно
для каждого
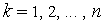 выполняем
следующие действия:
выполняем
следующие действия:
3.1) выполняем локальную вариацию
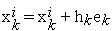 ;
;3.2) если полученная в результате новая точка
 является
допустимой (т.е.
является
допустимой (т.е.
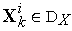 ),
то переходим к следующему пункту.
Иначе переходим к п.3.4;
),
то переходим к следующему пункту.
Иначе переходим к п.3.4;3.3) на интервалах
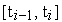 ,
,
 выполняем
элементарные
операциии определяем их "цены"
выполняем
элементарные
операциии определяем их "цены"
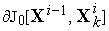 ,
,
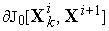 .
Если данная локальная
вариациябыла успешной — привела
к уменьшениюкритерия
качества управления(5)
.
Если данная локальная
вариациябыла успешной — привела
к уменьшениюкритерия
качества управления(5)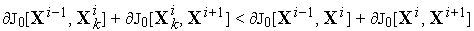 то
полагаем
то
полагаем
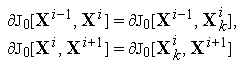 и
переходим к следующему пункту;
и
переходим к следующему пункту;3.4) выполняем локальную вариацию
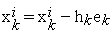 ;
;3.5) если полученная в результате новая точка
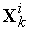 является
допустимой (т.е.
является
допустимой (т.е.
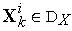 ),
то переходим к следующему пункту.
Иначе, полагаем
),
то переходим к следующему пункту.
Иначе, полагаем
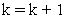 переходим
к п.3.1.
переходим
к п.3.1.3.6) выполняем действия, указанные в п.3.3.
Проверяем
выполнение условия окончания итераций
(см. ниже). Если это условие выполнено,
то в качестве приближения к оптимальной
траектории
![]() принимаем
текущую траекторию
принимаем
текущую траекторию
![]() ,
а в качестве приближения к оптимальному
управлению
,
а в качестве приближения к оптимальному
управлению
![]() —
управления, найденные при выполнении
элементарных
операций, соответствующих траектории
—
управления, найденные при выполнении
элементарных
операций, соответствующих траектории
![]() .
Иначе полагаем
.
Иначе полагаем
![]() и
переходим к п.2
и
переходим к п.2![]()
В качестве условия окончания итераций используется равенство нулю количества удачных локальных вариацийпосле данной итерации.
Действия,
указанные в пункте 3 приведенной схемы
метода
локальных вариаций, будем называть
основным циклом метода локальных
вариаций. Легко видеть, что временная
сложность основного цикла равна
![]() .
.
В изложенном виде метод локальных вариацийобладает рядом серьезных недостатков. Назовем основные из этих недостатков:
Существование тупиковых ситуаций — во множестве локальных вариацийне оказывается удачной не потому, что данная траектория оптимальна, а потому, что исследуются не все возможные вариации траектории, а только чрезвычайно узкое множество соседних с данной.
Медленная сходимость.
Трудность построения элементарной операции.
Указанные недостатки приводят к тому, что в изложенном виде метод локальных вариацийиспользуется редко. В вычислительной практике используются различные модификации метода локальных вариаций — метод дробных шагов, метод бегущей волны, метод трубки и др.
12.5 Решение задачи оптимального управления методом вариаций в пространстве управлений
Метод разработан в ИПМ АН СССР Федоренко Р.П.
Рассмотрим задачу оптимального управления
|
|
(1) |
|
|
(2) |
Обратим
внимание на то, что данная постановка
задачи
оптимального управленияне содержит
граничного условия
![]() и
ограничений на вектор фазовых координат
и
ограничений на вектор фазовых координат
![]() .
Заметим также, что поскольку вектор
фазовых координат
.
Заметим также, что поскольку вектор
фазовых координат
![]() при
фиксированных начальных условиях
при
фиксированных начальных условиях
![]() определятся
только управлением
определятся
только управлением
![]() ,
в число аргументов критерия
качества управления
,
в число аргументов критерия
качества управления
![]() можно
не включать вектор
можно
не включать вектор
![]() .
.
Положим,
что известно некоторое управление
![]() ,
которое мы будем называть невозмущенным
управлением.
,
которое мы будем называть невозмущенным
управлением.
В
рассматриваемом методе существенно
используется производная функционала
![]() .
Если для любых достаточно малых возмущений
.
Если для любых достаточно малых возмущений
![]() невозмущенного
управления
невозмущенного
управления
![]() справедливо
соотношение
справедливо
соотношение
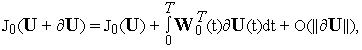
то
![]() называется
функциональной производной в смысле
Фреше функционала
называется
функциональной производной в смысле
Фреше функционала
![]() на
невозмущенной траектории
на
невозмущенной траектории
![]() и
обозначается
и
обозначается
|
|
(3) |
Здесь
![]() —
—
![]() -вектор-столбец,
-вектор-столбец,
![]() —
—
![]() -вектор-строка
(транспонированный вектор
-вектор-строка
(транспонированный вектор
![]() ),
),
![]() —
некоторая векторная норма.
—
некоторая векторная норма.
Техника дифференцирования функционалов, определенных на траекториях динамической системы, достаточно сложна и ее рассмотрение выходит за рамки данного курса. Будем полагать, однако, что мы умеем вычислять функциональные производные (3).
Заметим, что метод вариаций в пространстве управленийприменим и к функционалам, отличным от функционала (2), например, к функционалу вида
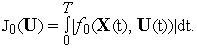
По существу, при этом изменяется лишь техника вычисления функциональных производных.
В
методе
вариаций в пространстве управленийна каждой итерации вариация
![]() управления
управления
![]() определяется
путем минимизации линейной части
приращения функционала
определяется
путем минимизации линейной части
приращения функционала
![]() ,
вызванного этой вариаций:
,
вызванного этой вариаций:
|
|
(4) |
Здесь
![]() —
некоторая малая окрестность невозмущенного
управления
—
некоторая малая окрестность невозмущенного
управления
![]() .
.
Окрестность
![]() имеет
важное технологическое значение –
удачное построение этой окрестности
может значительно повысить вычислительную
эффективность метода. Однако задача
построения этой окрестности однозначного
решения не имеет.
имеет
важное технологическое значение –
удачное построение этой окрестности
может значительно повысить вычислительную
эффективность метода. Однако задача
построения этой окрестности однозначного
решения не имеет.
При
построении множества
![]() следует
учитывать следующие требования:
следует
учитывать следующие требования:
Из того факта, что
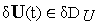 ,
должно следовать, что
,
должно следовать, что
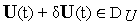 ;
;Множество
 должно
быть достаточно малой окрестностью
траектории
должно
быть достаточно малой окрестностью
траектории
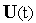 ,
чтобы линейная часть
,
чтобы линейная часть
 приращения
функционала
приращения
функционала
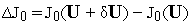 достаточно
точно описывала это приращение;
достаточно
точно описывала это приращение;Множество
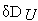 должно
быть достаточно большой окрестностью
траектории
должно
быть достаточно большой окрестностью
траектории
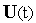 ,
чтобы сходимость управления к оптимальному
управлению не была слишком медленной;
,
чтобы сходимость управления к оптимальному
управлению не была слишком медленной;Множество
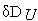 должно
быть полной окрестностью невозмущенного
управления
должно
быть полной окрестностью невозмущенного
управления
 .
Окрестность
.
Окрестность
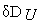 траектории
траектории
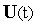 называется
полной, если для любой допустимой
вариации управления
называется
полной, если для любой допустимой
вариации управления
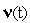 (т.е.
такой вариации, что
(т.е.
такой вариации, что
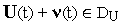 )
существует такое число
)
существует такое число
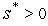 ,
что
,
что
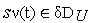 для
всех
для
всех
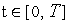 и
для всех
и
для всех
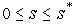 .
Понятие полной окрестности формализует
требование полноты допустимых вариаций
– окрестность
.
Понятие полной окрестности формализует
требование полноты допустимых вариаций
– окрестность
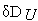 должна
содержать вариации невозмущенного
управления во всех допустимых
направлениях.
должна
содержать вариации невозмущенного
управления во всех допустимых
направлениях.
Общая схема метода вариаций в пространстве управлений.
Из каких либо соображений задаем начальное приближение к оптимальному управлению
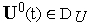 и
полагаем счетчик числа итераций равным
.
и
полагаем счетчик числа итераций равным
.С управлением
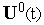 решаем
задачу Коши для системы ОДУ (1) – получаем
фазовую траекторию
решаем
задачу Коши для системы ОДУ (1) – получаем
фазовую траекторию
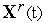 .
.Вычисляем
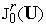 —
значение критерия
качества управления(2) на невозмущенной
траектории
—
значение критерия
качества управления(2) на невозмущенной
траектории
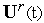 .
.В окрестности невозмущенной траектории
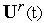 выполняем
линеаризацию задачи – вычисляем
функциональную производную
выполняем
линеаризацию задачи – вычисляем
функциональную производную
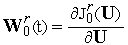 и
определяем окрестность
и
определяем окрестность
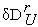 невозмущенной
траектории.
невозмущенной
траектории.Из условия
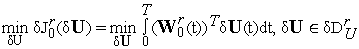
(5)
находим приращение
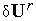 управления
управления
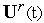 .
.Полагаем
 .
.Если условие окончания итераций выполнено (см. ниже), то в качестве приближения к оптимальному управлению принимаем управление
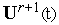 и
заканчиваем вычисления. Иначе – полагаем
и
заканчиваем вычисления. Иначе – полагаем
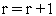 и
переходим к п.2
и
переходим к п.2
В качестве условия окончания итераций естественно принять условие
![]()
где
![]() —
некоторая функциональная норма,
—
некоторая функциональная норма,
![]() заданная
константа.
заданная
константа.
Заметим, что задача (5) может быть сведена к задаче линейного программирования, что является значительным достоинством метода.
12.6 Метод динамического программирования Беллмана
Идею метода динамического программирования Беллманарассмотрим на примерезадачи оптимального быстродействия
|
|
(1) |
|
|
(2) |
Гипотеза
1. Какова бы ни была отличная от
![]() допустимая
точка фазового пространства, существует
оптимальная (в смысле быстродействия)
траектория перехода динамической
системы из точки
допустимая
точка фазового пространства, существует
оптимальная (в смысле быстродействия)
траектория перехода динамической
системы из точки
![]() в
точку
в
точку
![]() (см.
рис. 1)
(см.
рис. 1)
|
|
Рис. 1. К гипотезе 1. (n = 2).
Время,
в течение которого осуществляется
оптимальный переход из точки
![]() в
точку
в
точку
![]() ,
обозначим
,
обозначим
![]() .
.
В
этих терминах гипотеза 1 может быть
сформулирована следующим образом. Для
любой точки
![]() существует
такое управление
существует
такое управление
![]() ,
под действием которого динамическая
система (1) переходит за время, равное
,
под действием которого динамическая
система (1) переходит за время, равное
![]() ,
из точки
,
из точки
![]() в
точку
в
точку
![]() ,
но за время, меньшее, чем
,
но за время, меньшее, чем
![]() ,
перейти из точки
,
перейти из точки
![]() в
точку
в
точку
![]() невозможно.
невозможно.
Гипотеза
2. Функция
![]() непрерывна
и всюду, кроме, быть может, точки
непрерывна
и всюду, кроме, быть может, точки
![]() ,
имеет непрерывные частные производные
,
имеет непрерывные частные производные
![]()
![]()
Пусть
теперь (![]() — оптимальный процесс перехода системы
(1) из состояния
— оптимальный процесс перехода системы
(1) из состояния
![]() в
состояние
в
состояние
![]() и
и
![]() —
отрезок времени, в течение которого
этот переход происходит;
—
отрезок времени, в течение которого
этот переход происходит;
![]() .
Другими словами, положим, что
.
Другими словами, положим, что
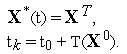
Утверждение
1 (принцип
оптимальности). Если процесс
![]() оптимален,
то процесс
оптимален,
то процесс
![]() также
оптимален.
также
оптимален.
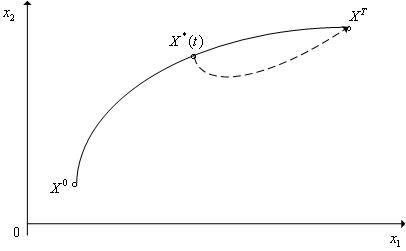
Доказательство
(см. рис. 2). Движение по рассматриваемой
оптимальной траектории от точки
![]() до
точки
до
точки
![]() осуществляется
за время
осуществляется
за время
![]() ,
а движение из точки
,
а движение из точки
![]() до
точки
до
точки
![]() —
в течение времени
—
в течение времени
![]() .
Быстрее, чем за это время из точки
.
Быстрее, чем за это время из точки
![]() попасть
в точку
попасть
в точку
![]() невозможно.
невозможно.
|
|
Рис. 2. К утверждению 1. (n = 2).
Действительно,
если бы такое движение существовало
(пунктир на рис. 2), то переместившись
из точки
![]() в
точку
в
точку
![]() за
время
за
время
![]() ,
а затем из точки
,
а затем из точки
![]() в
точку
в
точку
![]() быстрее,
чем за время
быстрее,
чем за время
![]() ,
мы осуществили бы переход из
,
мы осуществили бы переход из
![]() в
в
![]() за
время, меньшее, чем
за
время, меньшее, чем
![]() ,
что противоречит предположению об
оптимальности процесса
,
что противоречит предположению об
оптимальности процесса
![]()
![]()
Утверждение
2. Если процесс
![]() оптимален,
то справедливо уравнение
оптимален,
то справедливо уравнение
![]()
где
![]() называется
функцией Беллмана.
называется
функцией Беллмана.
Доказательство.
Из принципа
оптимальностиследует, что
![]() есть
время оптимального движения из точки
есть
время оптимального движения из точки
![]() в
точку
в
точку
![]() ,
т.е.
,
т.е.
|
|
(3) |
Заменив
в формуле (3)
![]() на
на
![]() ,
получим
,
получим
![]()
или
|
|
(4) |
Переходя
в формуле (4) к пределу при
![]() ,
получим, что на оптимальной траектории
выполняется равенство
,
получим, что на оптимальной траектории
выполняется равенство
|
|
(5) |
По правилам дифференцирования сложной функции с учетом уравнения (1) из равенства (5) имеем
|
|
(6) |
Из
принципа
оптимальностиследует, что соотношение
(6) верно для любых
![]() .
Таким образом, окончательно имеем
.
Таким образом, окончательно имеем
![]()
![]()
Аналогично утверждению 2 можно доказать справедливость следующего утверждения.
Утверждение
3. Если процесс
![]() оптимален,
то справедливо уравнение
динамического программирования Беллмана
для непрерывной системы
оптимален,
то справедливо уравнение
динамического программирования Беллмана
для непрерывной системы
|
|
(7) |
Методом динамического программирования Беллмананазывается метод решениязадач оптимального управления, использующийпринцип оптимальностиили уравнение динамического программирования Беллмана.
Подчеркнем следующие обстоятельства:
уравнение динамического программирования Беллмана дает необходимое условие минимума;
уравнение динамического программирования Беллмана требует выполнения гипотезы 12.6.2 относительно неизвестной функции Беллмана
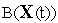 .
Однако, даже в простейших задачах
оптимального управленияфункция
.
Однако, даже в простейших задачах
оптимального управленияфункция
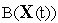 оказывается
не всюду дифференцируемой. По этой
причине при решении задач оптимального
управления методом динамического
программирования уравнение (7) в явном
виде не используется — используется
принцип
оптимальности.
оказывается
не всюду дифференцируемой. По этой
причине при решении задач оптимального
управления методом динамического
программирования уравнение (7) в явном
виде не используется — используется
принцип
оптимальности.
12.7 Решение задачи оптимального управления методом динамического программирования Беллмана
Рассмотрим (только для простоты записи) задачу оптимального управлениядля стационарной динамической системы икритерием оптимальности управления, зависящим только от вектора управления:
|
|
(1) |
|
|
(2) |
Обратим
внимание на то, что, в отличие от того,
как это делалось ранее, для обозначения
![]() фазового
вектора использована маленькая буква
фазового
вектора использована маленькая буква
![]() ,
а для обозначения
,
а для обозначения
![]() вектора
управления – маленькая буква
вектора
управления – маленькая буква
![]() .
.
Покроем
интервал
![]() сеткой
сеткой
![]() с
шагом
с
шагом
![]() (см.
рис. 1).
(см.
рис. 1).
|
|
Рис. 1. Равномерная временная сетка на интервале [0, T].
Систему ОДУ (1) заменим ее конечно-разностным аналогом
|
|
(3) |
а функционал (2) заменим его приближенным значением, вычисленным по формуле прямоугольников
|
|
(4) |
где
![]() есть
есть
![]() -матрица.
-матрица.
Таким образом, задача оптимального управления(1), (2) в дискретной форме имеет вид (3), (4).
Аналогично
матрице
![]() введем
в рассмотрение
введем
в рассмотрение
![]() -матрицу
-матрицу
![]() и
сформулируем принцип
оптимальности(см. параграф 12.6) для
задачи (3), (4).
и
сформулируем принцип
оптимальности(см. параграф 12.6) для
задачи (3), (4).
Утверждение
1 (принцип
оптимальностидля дискретной системы).
Пусть
![]() —
оптимальное управление для задачи
оптимального управления(3), (4) и пусть
—
оптимальное управление для задачи
оптимального управления(3), (4) и пусть
![]() —
соответствующая оптимальная фазовая
траектория. Тогда для любых
—
соответствующая оптимальная фазовая
траектория. Тогда для любых
![]() управление
управление
![]() и
соответствующая траектория
и
соответствующая траектория
![]() будут
оптимальными на интервале времени
будут
оптимальными на интервале времени
![]()
![]()
Другими
словами, если траектория
![]() оптимальна,
то и любая ее завершающая часть,
начинающаяся из точки
оптимальна,
то и любая ее завершающая часть,
начинающаяся из точки
![]() ,
будет оптимальной на последних
,
будет оптимальной на последних
![]() шагах.
А всякая другая траектория из того же
состояния, вообще говоря, не является
оптимальной на этих шагах (см. рис. 2).
шагах.
А всякая другая траектория из того же
состояния, вообще говоря, не является
оптимальной на этих шагах (см. рис. 2).
|
|
Рис. 2. К принципу оптимальности для дискретной системы. n = 2.
Обозначим
значение функционала (4) на завершающих
![]() шагах
шагах
![]()
Тогда
если на завершающих
![]() шагах
управление оптимально, имеет место
равенство
шагах
управление оптимально, имеет место
равенство
|
|
(5) |
где
![]() —
функция Беллмана для дискретной системы
последних
—
функция Беллмана для дискретной системы
последних
![]() шагов
для дискретной задачи
оптимального управления(3), (4).
шагов
для дискретной задачи
оптимального управления(3), (4).
Из
утверждения 1 следует, что на последнем
шаге (когда
![]() )
)
|
|
(6) |
Найдем
рекуррентное соотношение, связывающее
между собой функции
![]() ,
,
![]() .
Положим для этого, что функция
.
Положим для этого, что функция
![]() известна.
Тогда если на
известна.
Тогда если на
![]() -ом
шаге с начальным состоянием
-ом
шаге с начальным состоянием
![]() выбрать
управление
выбрать
управление
![]() ,
то процесс перейдет в состояние
,
то процесс перейдет в состояние
![]() (начальное
для последующих
(начальное
для последующих
![]() шагов).
Если этот переход оптимален, то опять
же из утверждения 1 следует искомое
соотношение
шагов).
Если этот переход оптимален, то опять
же из утверждения 1 следует искомое
соотношение
|
|
(7) |
Уравнения
(6), (7) позволяют последовательно найти
функции
![]() и
называются уравнениями
динамического программирования Беллмана
для дискретной системы(3), (4). Отметим,
что одновременно с нахождением функций
и
называются уравнениями
динамического программирования Беллмана
для дискретной системы(3), (4). Отметим,
что одновременно с нахождением функций
![]() оказываются
определенными и управления
оказываются
определенными и управления
![]() .
Поскольку управление
.
Поскольку управление
![]() зависит
от состояния
зависит
от состояния
![]() ,
это управление называется условно
оптимальным управлением.
,
это управление называется условно
оптимальным управлением.
После
нахождения условно оптимальных управлений
![]() можно
найти искомые управления
можно
найти искомые управления
![]() по
следующей схеме:
по
следующей схеме:
поскольку состояние
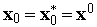 известно,
находим управление
известно,
находим управление
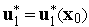 ;
с этим управлением по формуле (3) находим
состояние
;
с этим управлением по формуле (3) находим
состояние
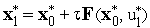 ;
;поскольку состояние
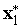 известно,
находим управление
известно,
находим управление
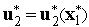 ;
с этим управлением по формуле (3) находим
состояние
;
с этим управлением по формуле (3) находим
состояние
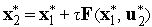 ;
;....
поскольку состояние
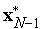 известно,
находим управление
известно,
находим управление
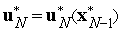 ;
очевидно, что
;
очевидно, что
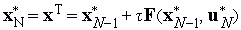 .
.
Схема метода приближённого решения задач оптимального управления методом динамического программирования Беллмана.
Этап 1
Шаг
1. Из условия (6) находим условно оптимальное
управление
![]() и
функцию Беллмана
и
функцию Беллмана
![]() .
.
Шаг
2. Используя результаты предыдущего
шага, из условия (7) находим условно
оптимальное управление
![]() и
функцию Беллмана
и
функцию Беллмана
![]() .
.
...
Шаг
N. Используя результаты предыдущего
шага, из условия (7) находим условно
оптимальное управление
![]() и
функцию Беллмана
и
функцию Беллмана
![]()
![]()
Этап 2.
Шаг
1. Находим управление
![]() и
состояние
и
состояние
![]() ;
;
Шаг
2. Находим управление
![]() и
состояние
и
состояние
![]() ;
;
...
Шаг
N. Находим управление
![]() и
состояние
и
состояние
![]()
![]()
Заметим,
что при приближённом решении задач
оптимального управленияметодом
динамического программирования остается
открытым вопрос о сходимости решения
![]() к
решению
к
решению
![]() исходной
непрерывной задачи оптимального
управления (1), (2).
исходной
непрерывной задачи оптимального
управления (1), (2).
Решение задачи оптимального управления методом динамического программирования Беллмана. Тест 1
Решите методом динамического программирования Беллманаследующуюзадачу оптимального управлениядля дискретной динамической системы (n=1, m=1):
|
|
(1) |
|
|
(2) |
где![]() — символ целой части числа (т.е. множество
— символ целой части числа (т.е. множество
![]() есть
множество целых числе от 0 до 4).
есть
множество целых числе от 0 до 4).
Ответ
Заменим ОДУ (1) его конечно-разностным аналогом
|
|
(3) |
а критерий оптимальности управления(2) — его приближенным значением, вычисленным по формуле прямоугольников
|
|
(4) |
Положим,
что
![]() ,
,
![]() .
.
Обратим
внимание на следующее обстоятельство:
из (3) и условия
![]() следует,
что фазовая переменная
следует,
что фазовая переменная
![]() может
принимать только целочисленные значения
на интервале
может
принимать только целочисленные значения
на интервале
![]() .
.
Этап 1.
Шаг
1 (![]() .
Из условия (4) находим условно оптимальное
управление
.
Из условия (4) находим условно оптимальное
управление
![]() и
функцию Беллмана
и
функцию Беллмана
![]() .
Поскольку, легко видеть,
.
Поскольку, легко видеть,
![]()
![]() и
и
![]() .
Сведем результаты вычисления значений
функции
.
Сведем результаты вычисления значений
функции
![]() в
табл. 1
в
табл. 1
Таблица 1
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
2 |
1 |
0 |
|
|
|
16 |
9 |
4 |
1 |
0 |
Шаг
2 (![]() .
Используя результаты предыдущего шага,
из условия (4) находим условно оптимальное
управление
.
Используя результаты предыдущего шага,
из условия (4) находим условно оптимальное
управление
![]() и
функцию Беллмана
и
функцию Беллмана
![]() .
Сведем результаты вычисления значений
функции
.
Сведем результаты вычисления значений
функции
![]() в
табл. 2, в которой прочерки соответствуют
не допустимым управлениям, а значения
управления и функции Беллмана, выделенные
жирным шрифтом, соответствует оптимальной
траектории.
в
табл. 2, в которой прочерки соответствуют
не допустимым управлениям, а значения
управления и функции Беллмана, выделенные
жирным шрифтом, соответствует оптимальной
траектории.
Таблица 2
|
|
|
|
|
|
|
|
|
|
|
|
- |
- |
- |
- |
|
|
|
|
- |
- |
- |
- |
|
|
|
1 |
|
- |
- |
- |
|
|
|
10 |
|
- |
- |
- |
|
|
|
2 |
1 |
|
- |
- |
|
|
|
8 |
5 |
|
- |
- |
|
|
|
3 |
2 |
1 |
|
- |
|
|
|
10 |
5 |
2 |
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим,
для примера, схему получения значений
![]() ,
,
![]() ,
соответствующих переходу системы из
состояния
,
соответствующих переходу системы из
состояния
![]() в
состояние
в
состояние
![]() .
Из состояния
.
Из состояния
![]() в
состояние
в
состояние
![]() система
переходит под действием управления
система
переходит под действием управления
![]() и
этому переходу соответствует значение
функции Беллмана
и
этому переходу соответствует значение
функции Беллмана
![]() ,
равное
,
равное
![]() (см.
табл. 1). Переход системы из состояния
(см.
табл. 1). Переход системы из состояния
![]() в
состояние
в
состояние
![]() может
быть выполнен только под действием
управления
может
быть выполнен только под действием
управления
![]() .
Поэтому
.
Поэтому
![]() .
.
Шаг
3
![]() .
Используя результаты предыдущего шага,
из условия (4) находим условно оптимальное
управление
.
Используя результаты предыдущего шага,
из условия (4) находим условно оптимальное
управление
![]() и
функцию Беллмана
и
функцию Беллмана
![]() .
Сведем результаты вычисления значений
функции
.
Сведем результаты вычисления значений
функции
![]() в
табл. 3, в которой прочерки соответствуют
не допустимым управлениям, а значения
управления и функции Беллмана, выделенные
жирным шрифтом, соответствует оптимальной
траектории.
в
табл. 3, в которой прочерки соответствуют
не допустимым управлениям, а значения
управления и функции Беллмана, выделенные
жирным шрифтом, соответствует оптимальной
траектории.
Таблица 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
10 |
|
|
|
2 |
|
|
|
8 |
|
|
|
3 |
|
|
|
10 |
|
|
|
|
|
|
|
|
Рассмотрим,
для примера, схему получения значений
![]() ,
,
![]() ,
соответствующих переходу системы из
состояния
,
соответствующих переходу системы из
состояния
![]() в
состояние
в
состояние
![]() .
Из состояния
.
Из состояния
![]() система
может перейти оптимально в состояние
система
может перейти оптимально в состояние
![]() или
в состояние
или
в состояние
![]() Первому
переходу соответствует оптимальное
управление
Первому
переходу соответствует оптимальное
управление
![]() ,
второму переходу – оптимальное управление
,
второму переходу – оптимальное управление
![]() .
Указанным переходам соответствует
значение функции Беллмана
.
Указанным переходам соответствует
значение функции Беллмана
![]() ,
равное
,
равное
![]() (см.
табл. 2). Переход системы из состояния
(см.
табл. 2). Переход системы из состояния
![]() в
состояние
в
состояние
![]() может
быть выполнен только под действием
управления
может
быть выполнен только под действием
управления
![]() .
Поэтому
.
Поэтому
![]() .
.
Этап 2.
Шаг
4. Из табл. 3 следует, что существует
два равноценных (приводящих к значению
функции Беллмана, равному
![]() )
оптимальных управления
)
оптимальных управления
![]() .
По формуле
.
По формуле
![]() находим
соответствующие значения переменной
состояния
находим
соответствующие значения переменной
состояния
![]() :
:
![]()
![]()
Шаг
5. Из табл. 2 следует, что для
![]() существует
два равноценных (приводящих к значению
функции Беллмана, равному
существует
два равноценных (приводящих к значению
функции Беллмана, равному
![]() )
управления
)
управления
![]() ,
,
![]() .
Аналогично, из табл. 2 следует, что
для
.
Аналогично, из табл. 2 следует, что
для
![]() существует
одно оптимальное управление
существует
одно оптимальное управление
![]() .
По формуле
.
По формуле
![]() находим
соответствующие значения переменной
состояния
находим
соответствующие значения переменной
состояния
![]() :
:
![]()
![]()
![]()
Шаг
6. Из табл. 1 следует, что для
![]() существует
одно оптимальное управление
существует
одно оптимальное управление
![]() .
Аналогично, из табл. 1 следует, что
для
.
Аналогично, из табл. 1 следует, что
для
![]() существует
одно оптимальное управление
существует
одно оптимальное управление
![]() .
По формуле
.
По формуле
![]() находим
соответствующие значения переменной
состояния
находим
соответствующие значения переменной
состояния
![]() :
:
![]()
![]() .
.
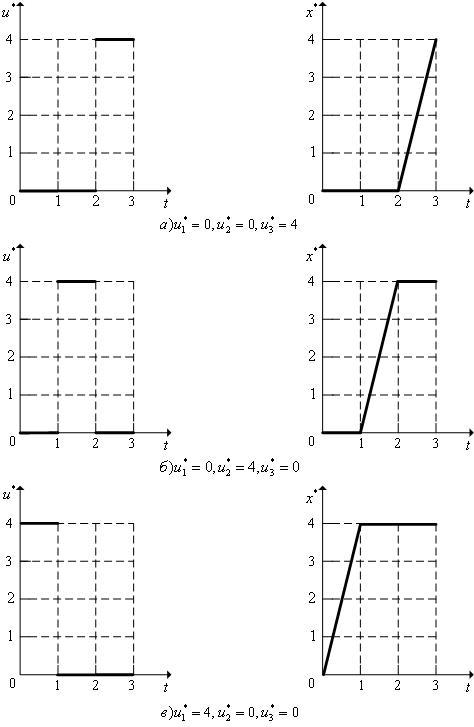
Полученные
оптимальные управления
![]() и
соответствующие оптимальные фазовые
траектории
и
соответствующие оптимальные фазовые
траектории
![]() иллюстрирует
рис. 1.
иллюстрирует
рис. 1.
|
|
Рис. 1.
12.8 Решение задачи оптимального управления методом сведения к задаче нелинейного программирования
Рассмотрим задачу оптимального управления
|
|
(1) |
|
|
(2) |
Обратим
внимание на то, что так же, как в предыдущем
параграфе, для обозначения
![]() фазового
вектора использована маленькая буква
фазового
вектора использована маленькая буква
![]() ,
а для обозначения
,
а для обозначения
![]() вектора
управления – маленькая буква
вектора
управления – маленькая буква
![]() .
.
Метод решения задачи оптимального управления(1), (2) путем сведения этой задачи кзадаче нелинейного программирования(метод сведения к задаче нелинейного программирования) рассматривался (на одном частном примере) в главе 1. Изложим общую схему этого метода.
Покроем
интервал
![]() равномерной
или неравномерной сеткой
равномерной
или неравномерной сеткой
![]() с
шагом
с
шагом
![]() (см.
рис. 1).
(см.
рис. 1).
|
|
Рис. 1. Временная сетка tk, k ∈ [0, N] на интервале [0, T].
Систему ОДУ (1) заменим ее конечно-разностным аналогом
|
|
(3) |
а критерий качества управления(2) заменим его приближенным значением, вычисленным по формуле прямоугольников
|
|
(4) |
где
![]() есть
есть
![]() -матрица.
-матрица.
Дискретная задача оптимального управления(3), (4) представляет собойзадачу нелинейного программирования
|
|
(5) |
где,
в отличие от рассматриваемой ранее
постановки задачи оптимизации,
используется не вектор
варьируемых параметров, а матрица
![]() варьируемых
параметров. Очевидно, что легко перейти
от
варьируемых
параметров. Очевидно, что легко перейти
от
![]() матрицы
варьируемых параметров
матрицы
варьируемых параметров
![]() к
привычному для нас
к
привычному для нас
![]() вектору
варьируемых параметров.
вектору
варьируемых параметров.
Приведем
схему вычисления значений критерия
оптимальности управления
![]() .
Пусть тем или иным способом заданы
значения элементов
.
Пусть тем или иным способом заданы
значения элементов
![]() матрицы
матрицы
![]() .
Тогда для вычисления соответствующего
значения критерия
.
Тогда для вычисления соответствующего
значения критерия
![]() необходимо
выполнить следующие действия:
необходимо
выполнить следующие действия:
при управлениях
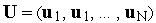 по
формуле (3) последовательно вычисляем
значения компонент вектора
по
формуле (3) последовательно вычисляем
значения компонент вектора
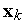 для
для
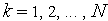 ;
;с найденными векторами
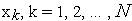 и
управлениями
и
управлениями
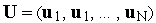 по
формуле (5) вычисляем значение критерия
оптимальности управления
по
формуле (5) вычисляем значение критерия
оптимальности управления
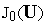 .
.
Задача нелинейного программирования(5) может быть решена рассмотренными ранееметодами условной оптимизации.
Изложенный
метод создает впечатление тривиальности
решения задач
оптимального управления. Действительно,
есть теоремы о том, что решение дискретной
задачи (3), (4) сколь угодно точно (при
![]() )
аппроксимирует решение исходной задачи
(1), (2). Есть теоремы о сходимости методов
оптимизации, с помощью которых может
быть найден минимум (4). Однако всегда
остаются открытыми вопросы: можно ли
данное
)
аппроксимирует решение исходной задачи
(1), (2). Есть теоремы о сходимости методов
оптимизации, с помощью которых может
быть найден минимум (4). Однако всегда
остаются открытыми вопросы: можно ли
данное
![]() считать
достаточно большим?; можно ли ограничиться
данным числом итераций при решении
задачи (4)?. Т.е. необходим тщательный
содержательный контроль результатов.
Иначе легко получить решения, сколь
угодно далекие от действительно
оптимальных решений. В целом, данный
метод (впрочем, как и любой другой) может
быть рекомендован только в комбинации
с другими методами.
считать
достаточно большим?; можно ли ограничиться
данным числом итераций при решении
задачи (4)?. Т.е. необходим тщательный
содержательный контроль результатов.
Иначе легко получить решения, сколь
угодно далекие от действительно
оптимальных решений. В целом, данный
метод (впрочем, как и любой другой) может
быть рекомендован только в комбинации
с другими методами.
Решение задачи оптимального управления путем сведения к задаче нелинейного программирования. Тест 1
Рассмотрим следующую двумерную (n = 2) задачу оптимального управленияс одномерным (m = 1) вектором управления
|
|
(1) |
![]()
|
|
(2) |
где
![]() —
заданные скалярные константы, а
—
заданные скалярные константы, а
![]() —
заданная скалярная функция.
—
заданная скалярная функция.
Сведите эту задачу оптимального управлениякзадаче условной оптимизации.
Ответ
Заменим систему ОДУ (1) ее конечно-разностным аналогом:
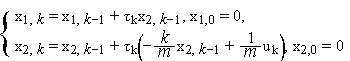
![]()
Заменим критерий качества управления(2) его приближенным значением, вычисленным по формуле прямоугольников:
![]()
где
![]() есть
есть
![]() -вектор
(поскольку
-вектор
(поскольку
![]() —
скалярная функция).
—
скалярная функция).
Таким
образом, задача
оптимального управления(1), (2) сведена
к следующей
![]() -мерной
задаче
условной оптимизации
-мерной
задаче
условной оптимизации
![]()
где
множество
допустимых значений вектора варьируемых
параметров
![]() .
.