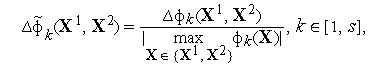- •Глава 1. Математическая формулировка задачи непрерывной оптимизации в конечномерном пространстве
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения
- •Глава 12. Задачи оптимального управления и методы их приближенного решения
- •Глава 1. Математическая формулировка задачи оптимального проектирования.
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации.
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения.
- •Глава 4. Методы поиска локального минимума одномерных функций.
- •Глава 5. Методы поиска глобального минимума одномерных функций.
- •Глава 6. Многомерная локальная безусловная оптимизация. Детерминированные прямые методы.
- •Глава 7. Многомерная локальная безусловная оптимизация. Детерминированные методы первого и второго порядков.
- •1. Постановка задачи.
- •2. Итерационная формула.
- •Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска (прямые методы).
- •Глава 9. Многомерная локальная условная оптимизация.
- •Глава 10. Многомерная глобальная условная оптимизация.
- •Глава 11. Задачи многокритериальной оптимизации и методы их решения.
- •Глава 12. Задачи оптимального управления и методы их приближенного решения.
Глава 11. Задачи многокритериальной оптимизации и методы их решения.
11.1 Постановка задачи многокритериальной оптимизацию. Множество Парето
В
задачах САПР часто возникает задача
обеспечить оптимальность объекта
проектирования одновременно по нескольким
критериям
оптимальности
![]() .
Обычно эти критерии противоречивы и
оптимизация по каждому из них приводит
к различным значениям вектора
варьируемых параметров
.
Обычно эти критерии противоречивы и
оптимизация по каждому из них приводит
к различным значениям вектора
варьируемых параметров
![]() .
Поэтому выделяется отдельный класс
задач
многокритериальной оптимизации.
.
Поэтому выделяется отдельный класс
задач
многокритериальной оптимизации.
Постановка задачи многокритериальной оптимизации.
Будем
называть каждый из скалярных критериев
оптимальности
![]() частным
критерием оптимальности. Совокупностьчастных
критериев оптимальности
частным
критерием оптимальности. Совокупностьчастных
критериев оптимальности
![]() будем
называть векторным
критерием оптимальности. Положим,
что ставится задача минимизации каждого
изчастных
критериев оптимальности ф1(
будем
называть векторным
критерием оптимальности. Положим,
что ставится задача минимизации каждого
изчастных
критериев оптимальности ф1(![]() ),
ф2(
),
ф2(![]() ),
... , фs(
),
... , фs(![]() )
в одной и той же области
допустимых значений
)
в одной и той же области
допустимых значений
![]() .
.
Решение
задачи
многокритериальной оптимизациив
общем случае не является оптимальным
ни для одного изчастных
критериев, а оказывается некоторым
компромиссом для вектора
![]() в
целом.
в
целом.
Задачу многокритериальной оптимизациибудем записывать в виде
|
|
(1) |
где
![]() —
множество
допустимых значений вектора варьируемых
параметров
—
множество
допустимых значений вектора варьируемых
параметров
![]() .
.
Прежде,
чем применить тот или иной метод решения
задачи (1), обычно производят нормализацию
частных критериев, приводя все частные
критерии оптимальности
![]() к
одному масштабу. Чаще всего при этом
используют относительные отклонения
частных
критериевот их минимальных значений:
к
одному масштабу. Чаще всего при этом
используют относительные отклонения
частных
критериевот их минимальных значений:
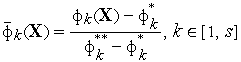
где
![]()
![]() Метод
относится к классу стохастических
методов оптимизации
Метод
относится к классу стохастических
методов оптимизации
Сохраним
за нормализованными частными
критериями оптимальностиобозначения
![]() .
.
Множество Парето.
Введем
понятие пространства
критериев
![]() .
Пространство критериев имеет размерность
.
Пространство критериев имеет размерность
![]() (по
числу частных критериев) и образуется
(по
числу частных критериев) и образуется
![]() ортогональными
осями координат, вдоль которых
откладываются значения частных
критериев оптимальности
ортогональными
осями координат, вдоль которых
откладываются значения частных
критериев оптимальности
![]() .
.
Векторный
критерий оптимальности
![]() выполняет
отображение множества
допустимых значений
выполняет
отображение множества
допустимых значений
![]() в
некоторую область
в
некоторую область
![]() ,
где
,
где
![]() —
пространство
варьируемых параметров(см. рис. 1).
—
пространство
варьируемых параметров(см. рис. 1).
|
|
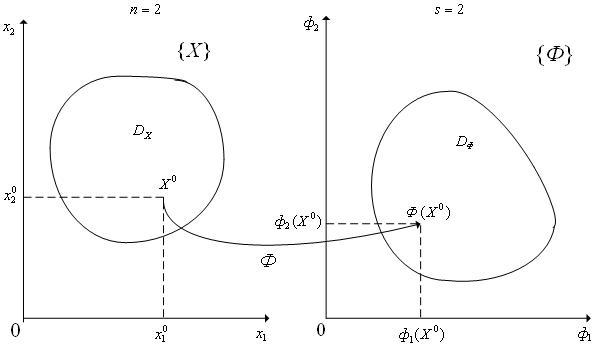
Рис. 1. К отображению векторным критерием оптимальности Φ(X) множества допустимых значений DX пространства варьируемых параметров {X} в область DΦ пространства критериев {Φ}. Случай n=2, s=2.
Введем
на множестве
![]() отношение
предпочтения.
отношение
предпочтения.
Отношение
предпочтения
![]() .
Будем говорить, что вектор
.
Будем говорить, что вектор
![]() предпочтительнее
вектора
предпочтительнее
вектора
![]() ,
и писать
,
и писать
![]() ,
если среди равенств и неравенств
,
если среди равенств и неравенств
![]()
имеется хотя бы одно строгое неравенство (см. рис. 2).
Аналогично
на множестве
![]() введем
отношение
доминирования: будем говорить, чтовекторный
критерий оптимальности
введем
отношение
доминирования: будем говорить, чтовекторный
критерий оптимальности
![]() доминирует
векторный критерий оптимальности
доминирует
векторный критерий оптимальности
![]() ,
и писать
,
и писать
![]() ,
если
,
если
![]() (см.
рис. 2).
(см.
рис. 2).
Примечание 1
Введенные отношение предпочтенияиотношение доминированияявляются транзитивными, т.е.
если
![]() и
и
![]() ,
то
,
то
![]() ;
;
если
![]() )
и
)
и
![]() (
(![]() ,
то
,
то
![]() (
(![]() .
.
|
|
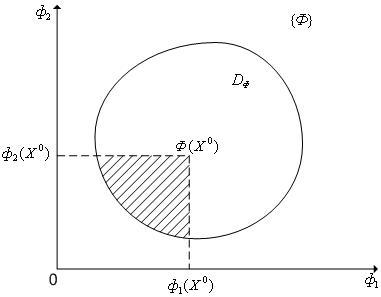
Рис. 2. К понятию отношения предпочтения и отношения доминирования (s = 2). Для всех точек заштрихованной области Ф(X1) ⊳ Ф(X2), т.е. заштрихованной области пространства критериев соответствуют векторы варьируемых параметров X ∈ DФ, для которых X1 ⊱ X2.
Выделим
из множества
![]() подмножество
подмножество
![]() точек,
для которых нет точек, их доминирующих.
Множество
точек,
для которых нет точек, их доминирующих.
Множество
![]() ,
соответствующее
,
соответствующее
![]() ,
называется множеством
Парето(переговорным
множеством,областью
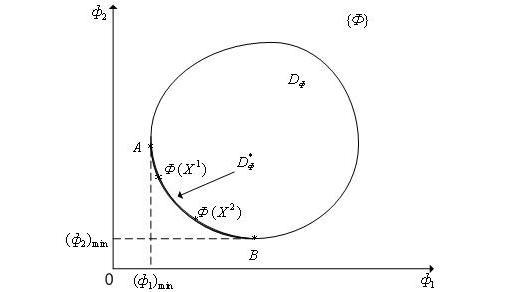
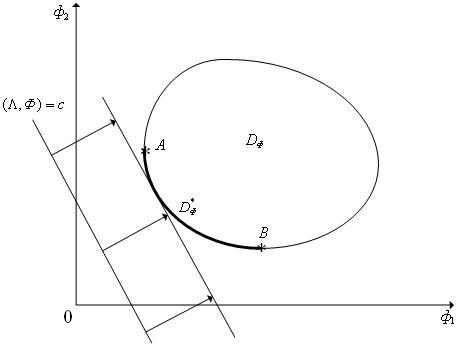
компромисса) — см. рис. 3. Поскольку
множество DФ
на рисунке является выпуклым, то множество
D
,
называется множеством
Парето(переговорным
множеством,областью
компромисса) — см. рис. 3. Поскольку
множество DФ
на рисунке является выпуклым, то множество
D![]() - есть часть границы множества DФ
— дуга AB, в которой точка A соответствует
(ф2)min,
а точка B — (ф1)min.
Среди точек
- есть часть границы множества DФ
— дуга AB, в которой точка A соответствует
(ф2)min,
а точка B — (ф1)min.
Среди точек
![]() (X1)
(X1)
![]() D*Ф,
D*Ф,
![]() (X2)
(X2)
![]() D*Ф
нет более предпочтительных, поскольку
ф1(X1)
> ф1(X2),
но ф2(X1)
> ф2(X2).
D*Ф
нет более предпочтительных, поскольку
ф1(X1)
> ф1(X2),
но ф2(X1)
> ф2(X2).
Таким
образом, если
![]() ,
то
,
то
![]()
Другими словами множество Паретоможно определить как множество, в котором значение любого изчастных критериев оптимальностиможно улучшить только за счет ухудшения других частных критериев – любое из решений, принадлежащее множеству Парето, не может быть улучшено одновременно по всем частным критериям.
|
|
Рис. 3. К определению множества Парето (s = 2).
Пример 1
Пусть
множество
допустимых значений
![]() (см.
рис. 4) и заданы два частных
критерия оптимальности
(см.
рис. 4) и заданы два частных
критерия оптимальности
![]() ,
,
![]() .
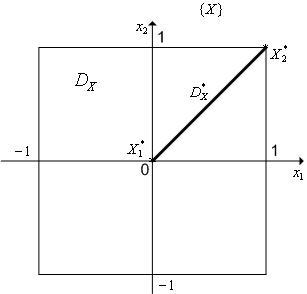
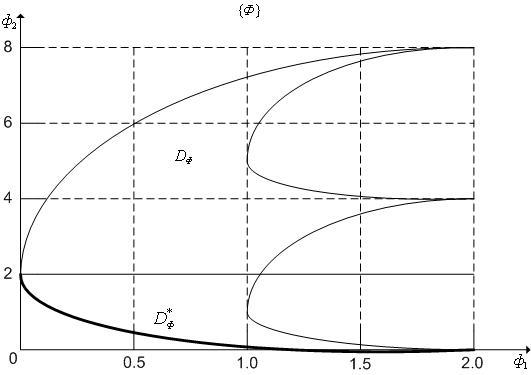
Можно показать, что множество
.
Можно показать, что множество
![]() при
этом имеет вид, представлены на рис. 5,
а множество
Парето
при
этом имеет вид, представлены на рис. 5,
а множество
Парето
![]() представляет
собой отрезок прямой, соединяющий точки
представляет
собой отрезок прямой, соединяющий точки
![]() ,
,
![]() —
см. рис. 4.
—
см. рис. 4.
|
|
Рис. 4. К прим. 1.
|
|
Рис. 5. К прим. 1.
Заметим,
что точки
![]() ,
,
![]() являются
точками минимума частных
критериев оптимальности
являются
точками минимума частных
критериев оптимальности
![]() ,
,
![]() ,
соответственно.
,
соответственно.
Роль множества Паретопри решениизадач многокритериальной оптимизацииопределяется следующей теоремой.
Теорема
1. Если для некоторых весовых множителей
![]() и
вектора
и
вектора
![]() имеет
место равенство
имеет
место равенство
|
|
(2) |
то
вектор
![]() оптимален
по Парето, т.е.
оптимален
по Парето, т.е.
![]() .
.
Доказательство.
Пусть вектор
![]() не
оптимален по Парето. Тогда существует
такой вектор
не
оптимален по Парето. Тогда существует
такой вектор
![]() ,
что
,
что
|
|
(3) |
причем
хотя бы одно из неравенств строгое.
Умножая каждое из неравенств (3) на
![]() и
складывая, получим
и
складывая, получим
![]()
что
противоречит условию теоремы![]()
Теорема
1 доказана для случая неотрицательных
весовых коэффициентов
![]() ,
хотя не содержит этого условия. Однако
доказательство возможно и для произвольных
весовых коэффициентов.
,
хотя не содержит этого условия. Однако
доказательство возможно и для произвольных
весовых коэффициентов.
Теорема показывает, что выбор определенной точки из множества Паретоэквивалентен указанию весов для каждого изчастных критериев оптимальности. На этом факте основано большое количество численных методов решениязадач многокритериальной оптимизации.
Заметим,
что теорема 1 задает лишь необходимое
условие оптимальности по Парето вектора
![]() .
Т.е. из того факта, что точка
.
Т.е. из того факта, что точка
![]() принадлежит
множеству
Парето, не следует, что эта точка
обязательно удовлетворяет условию (2).
принадлежит
множеству
Парето, не следует, что эта точка
обязательно удовлетворяет условию (2).
В
постановке задачи
многокритериальной оптимизации(1)
фиксируется лишьмножество
допустимых значений
![]() и
вектор частных
критериев
и
вектор частных
критериев
![]() .Этой
информации недостаточно для однозначного
решения задачи (1). Указанная информация
позволяет лишь выделить соответствующее
множество
Парето(можно сказать, что решением
задачи многокритериальной оптимизации
в постановке (1) является множество
Парето). Для однозначного решения задачи
(1) нужна дополнительная информация.
.Этой
информации недостаточно для однозначного
решения задачи (1). Указанная информация
позволяет лишь выделить соответствующее
множество
Парето(можно сказать, что решением
задачи многокритериальной оптимизации
в постановке (1) является множество
Парето). Для однозначного решения задачи
(1) нужна дополнительная информация.
Множество Парето. Тест 1
Используя
покрытие множества
допустимых значений вектора варьируемых
параметров
![]() ,
постройте приближенно множество
Паретодля следующей задачи
двухкритериальной оптимизации
,
постройте приближенно множество
Паретодля следующей задачи
двухкритериальной оптимизации
![]() :
:
![]()
![]()
![]() .
.
Изобразите
на рисунках множества
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Ответ
1.
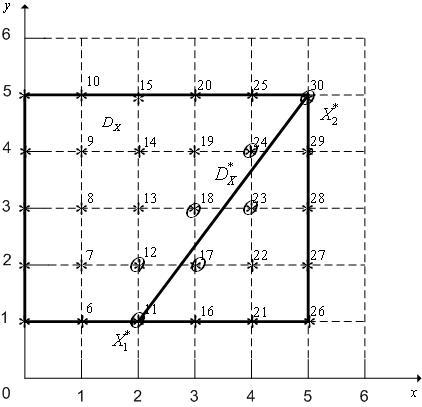
Покрываем множество
![]() равномерной
сеткой с шагом, равным 1 по обеим
координатным направлениям, и пронумеруем
узлы сетки так, как показано на рис. 1
(на рисунке звездочками выделены узлы
сетки, кружками – точки, соответствующие
множеству
равномерной
сеткой с шагом, равным 1 по обеим
координатным направлениям, и пронумеруем
узлы сетки так, как показано на рис. 1
(на рисунке звездочками выделены узлы
сетки, кружками – точки, соответствующие
множеству
![]() ).
).
|
|
Рис. 1.
2.
Вычисляем значения частных
критериев оптимальности
![]() ,
,
![]() в
узлах построенной сетки и заносим их в
табл. 1.
в
узлах построенной сетки и заносим их в
табл. 1.
Таблица 1
|
x |
y |
|
|
Номер узла |
|
0 |
1 |
4 |
41 |
1 |
|
0 |
2 |
5 |
34 |
2 |
|
0 |
3 |
8 |
29 |
3 |
|
0 |
4 |
13 |
26 |
4 |
|
0 |
5 |
20 |
25 |
5 |
|
1 |
1 |
1 |
32 |
6 |
|
1 |
2 |
2 |
25 |
7 |
|
1 |
3 |
5 |
20 |
8 |
|
1 |
4 |
10 |
17 |
9 |
|
1 |
5 |
17 |
16 |
10 |
|
2 |
1 |
0 |
25 |
11 |
|
2 |
2 |
1 |
18 |
12 |
|
2 |
3 |
4 |
13 |
13 |
|
2 |
4 |
9 |
10 |
14 |
|
2 |
5 |
16 |
9 |
15 |
|
3 |
1 |
1 |
20 |
16 |
|
3 |
2 |
2 |
13 |
17 |
|
3 |
3 |
5 |
8 |
18 |
|
3 |
4 |
10 |
5 |
19 |
|
3 |
5 |
17 |
4 |
20 |
|
4 |
1 |
4 |
17 |
21 |
|
4 |
2 |
5 |
10 |
22 |
|
4 |
3 |
8 |
5 |
23 |
|
4 |
4 |
13 |
2 |
24 |
|
4 |
5 |
20 |
1 |
25 |
|
5 |
1 |
9 |
16 |
26 |
|
5 |
2 |
10 |
9 |
27 |
|
5 |
3 |
13 |
4 |
28 |
|
5 |
4 |
18 |
1 |
29 |
|
5 |
5 |
25 |
0 |
30 |
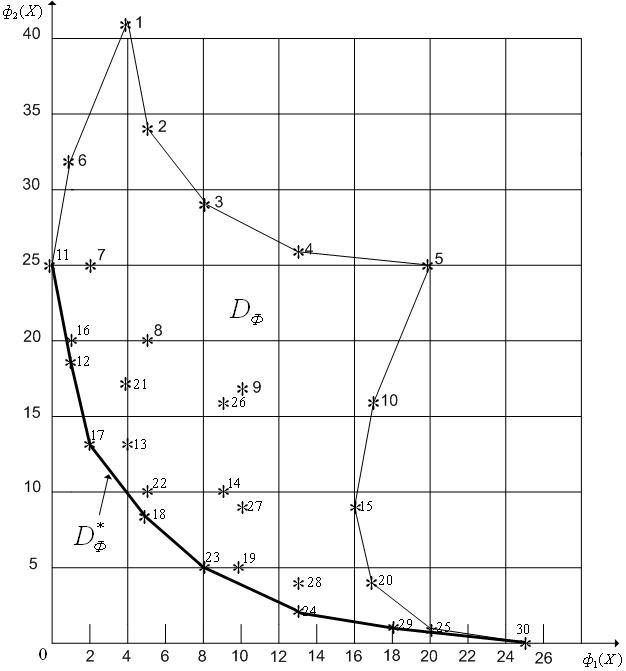
3.
Отображаем вычисленные значения частных
критериев оптимальности
![]() ,
,
![]() в
системе координат
в
системе координат
![]() (см.рис. 2).
(см.рис. 2).
|
|
Рис. 2.
4.
На рис. 2 аппроксимируем границу
множество
![]() ломаной
и выделяем множество
ломаной
и выделяем множество
![]() .
.
5.
Отмечаем точки, соответствующие множеству
![]() ,
на множестве
,
на множестве
![]() и
аппроксимируем полученные точки отрезком
прямой. Этот отрезок прямой и представляет
собой приближение к искомому множеству
Парето(см. рис. 1).
и
аппроксимируем полученные точки отрезком
прямой. Этот отрезок прямой и представляет
собой приближение к искомому множеству
Парето(см. рис. 1).
11.2 Метод весовых множителей решения задачи многокритериальной оптимизации
Рассмотрим задачу многокритериальной оптимизации
|
|
(1) |
где
![]() —
векторный
критерий оптимальности,
—
векторный
критерий оптимальности,
![]() —
частные
критерии оптимальности(скалярные),
—
частные
критерии оптимальности(скалярные),
![]() .-
множество
допустимых значений вектора варьируемых
параметров.
.-
множество
допустимых значений вектора варьируемых
параметров.
Для решения задачи многокритериальной оптимизации(1) широко используются методы, основанные на сведении задачи многокритериальной оптимизации к задаче однокритериальной оптимизации. Рассмотрим один из методов этой группы методов —метод весовых множителей.
В
метод
весовых множителейдополнительной
информацией (относительно информации,
заданной в постановке задачи (1)) является
информация об относительной важностичастных
критериев. Метод требует, чтобы эта
информация была формализована в значениях
весовых множители
![]() .
В этом случае в качестве скалярного
критерия используется критерий
.
В этом случае в качестве скалярного
критерия используется критерий
|
|
(2) |
Т.е. вместо задачи (1) решается многомерная задача условной оптимизациисо скалярнымкритерием оптимальности(2)
|
|
(3) |
Напомним
следующее: из теоремы 1 (см. параграф 1
данной главы) вытекает, что вектор
![]() ,
являющийся решением задачи
условной оптимизации(3), принадлежитмножеству
Паретозадачи (1), а обратное утверждение
неверно — вектор
,
являющийся решением задачи
условной оптимизации(3), принадлежитмножеству
Паретозадачи (1), а обратное утверждение
неверно — вектор
![]() ,
принадлежащий множеству Парето задачи
(1), не обязательно удовлетворяет условию
(3).
,
принадлежащий множеству Парето задачи
(1), не обязательно удовлетворяет условию
(3).
Существуют
различные способы выбора весовых
множители
![]() .
Одним из таких способов является
назначение коэффициентов в зависимости
от относительной важности соответствующих
частных критериев
оптимальности, например, согласно
табл. 1.
.
Одним из таких способов является
назначение коэффициентов в зависимости
от относительной важности соответствующих
частных критериев
оптимальности, например, согласно
табл. 1.
Таблица 1
|
Относительная важность критерия |
Определение относительной важности критериев |
|
1 |
Равная важность |
|
3 |
Умеренное (слабое) превосходство |
|
5 |
Сильное (существенное) превосходство |
|
7 |
Очевидное превосходство |
|
9 |
Абсолютное (подавляющее) превосходство |
|
2,4,6,8 |
Промежуточные решения между двумя соседними оценками |
Шкала относительной важности частных критериев.
Для
того чтобы при выборе весовых множителей
![]() избавиться
от влияния масштабов частных
критериев оптимальности, вметоде
весовых множителейцелесообразно
использовать нормализованные критерии.
избавиться
от влияния масштабов частных
критериев оптимальности, вметоде
весовых множителейцелесообразно
использовать нормализованные критерии.
Дадим
геометрическую интерпретацию метода.
Введем в рассмотрение
![]() вектор
вектор
![]() .
Тогда критерий
оптимальности(2) можно записать в
виде скалярного произведения
.
Тогда критерий
оптимальности(2) можно записать в
виде скалярного произведения
|
|
(4) |
а задачу (3) в виде
|
|
(5) |
Уравнение
![]() ,
где
,
где
![]() —
некоторая константа, определяет в
пространстве
критериев
—
некоторая константа, определяет в
пространстве
критериев
![]() гиперплоскость.
При этом решение задачи (5) можно
интерпретировать как поиск такого
значения
гиперплоскость.
При этом решение задачи (5) можно
интерпретировать как поиск такого
значения
![]() ,
при котором гиперплоскость
,
при котором гиперплоскость
![]() будет
касательной к множеству
будет
касательной к множеству
![]() задачи
(1). Компоненты вектора
задачи
(1). Компоненты вектора
![]() определяют
искомую точку касания этой гиперплоскости
с множеством
определяют
искомую точку касания этой гиперплоскости
с множеством
![]() (см.
рис. 1). На рис. 1 для любой точки
(см.
рис. 1). На рис. 1 для любой точки
![]() множества
множества
![]() (дуга
A,B) найдется вектор весовых множителей
(дуга
A,B) найдется вектор весовых множителей
![]() =
(λ1,
λ2,
... , λs),
при котором эта точка удовлетворяет
условию (5).
=
(λ1,
λ2,
... , λs),
при котором эта точка удовлетворяет
условию (5).
|
|
Рис. 1. Геометрическая интерпретация метода весовых множителей: случай двух критериев; множество DФ выпукло.
Множество
![]() задачи
(1) может быть не выпуклым. В этом случае
не все точки множества
задачи
(1) может быть не выпуклым. В этом случае
не все точки множества
![]() могут
быть достигнуты с помощью изменения
весовых множителей
могут
быть достигнуты с помощью изменения
весовых множителей
![]() (см.
рис. 2). На рис. 2 ни для одной точки
(см.
рис. 2). На рис. 2 ни для одной точки
![]() множества
множества
![]() ,
принадлежащей дуге A1B1,
невозможно найти вектор весовых
множителей
,
принадлежащей дуге A1B1,
невозможно найти вектор весовых
множителей
![]() =
(λ1,
λ2,
... , λs),
при котором эта точка удовлетворяет
условию (5).
=
(λ1,
λ2,
... , λs),
при котором эта точка удовлетворяет
условию (5).
|
|
Рис. 2. Геометрическая интерпретация метода весовых множителей: случай двух критериев; множество DФ не выпукло.
11.3 Метод эпсилон-ограничений решения задачи многокритериальной оптимизации
Рассмотрим задачу многокритериальной оптимизации
|
|
(1) |
где
![]() —
векторный
критерий оптимальности,
—
векторный
критерий оптимальности,
![]() —
частные
критерии оптимальности(скалярные),
—
частные
критерии оптимальности(скалярные),
![]() —
множество
допустимых значений вектора варьируемых
параметров.
—
множество
допустимых значений вектора варьируемых
параметров.
Метод ε-ограниченийотносится к группе методов, основанных на сведениизадачи многокритериальной оптимизациик однокритериальной многомернойзадаче условной оптимизации.
В
метод
ε-ограниченийв качестве скалярногокритерия
оптимальности
![]() используется
самый важный из частных
критериев оптимальности
используется
самый важный из частных
критериев оптимальности
![]() ,
а остальные частные критерии учитываются
с помощью ограничений типа неравенств
вида
,
а остальные частные критерии учитываются
с помощью ограничений типа неравенств
вида
![]() .
.
Дополнительной информацией в методе ε-ограниченийявляется информация о номере самого важного изчастных критериев, а также информация о максимально допустимых значения частных критериев .
Таким
образом, в методе
![]() -ограничений
вместо задачи (1) решается задача
условной оптимизациисо скалярнымкритерием
оптимальности
-ограничений
вместо задачи (1) решается задача
условной оптимизациисо скалярнымкритерием
оптимальности
![]() :
:
|
|
(2) |
где
|
|
(3) |
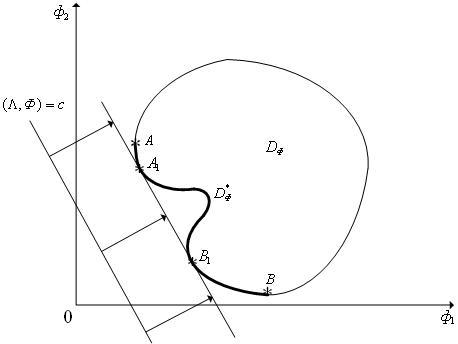
Метод
ε-ограниченийв значительной мере
свободен от указанного выше недостаткаметода
весовых множителейв случае, когда
множество
![]() не
выпукло (см. рис. 1). На рис. 1 точка
A2
в данном методе является доступной.
не
выпукло (см. рис. 1). На рис. 1 точка
A2
в данном методе является доступной.
|
|
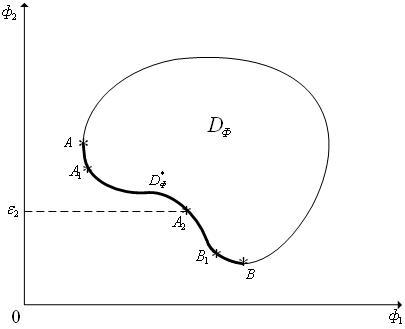
Рис. 1. Геометрическая интерпретация метода ε-ограничений: случай двух критериев; множество DФ не выпукло; самым важным является критерий ф1(X); на критерий ф2(X) наложено ограничение ф2(X) ≤ ε2.
Недостатком
метода
ε-ограниченийявляется трудность
выбора максимально допустимых значениячастных
критериев
![]() ,
которые гарантировали бы достижимость
некоторого решения. Кроме того, жесткость
ограничений
,
которые гарантировали бы достижимость
некоторого решения. Кроме того, жесткость
ограничений
![]() далеко
не всегда адекватна представлениям ЛПР
(лица, принимающего решения) о наилучшем
решении. Отметим также трудность
построения в явном или неявном виде
множества
далеко
не всегда адекватна представлениям ЛПР
(лица, принимающего решения) о наилучшем
решении. Отметим также трудность
построения в явном или неявном виде
множества
![]() .
.
11.4 Метод справедливого компромисса для решения задач многокритериальной оптимизации
Рассмотрим задачу многокритериальной оптимизации
|
|
(1) |
где
![]() —
векторный
критерий оптимальности,
—
векторный
критерий оптимальности,
![]() —
частные
критерии оптимальности(скалярные),
—
частные
критерии оптимальности(скалярные),
![]() —
множество
допустимых значений вектора варьируемых
параметров.
—
множество
допустимых значений вектора варьируемых
параметров.
Положим,
что все частные
критерии
![]() имеют
одинаковую важность!
имеют
одинаковую важность!
Справедливый компромисс.
Справедливым компромиссомбудем называть такой компромисс, при котором относительный уровень снижения качества по одному или несколькимчастным критериямне превосходит относительного уровня повышения качества по остальным частным критериям (меньше или равен).
Для
формализации понятия справедливого
компромиссанам понадобится ввести
отношение превосходства
![]() на
множестве
Парето(не путать сотношением
доминирования
на
множестве
Парето(не путать сотношением
доминирования
![]() ,
используемым при построении множества
Парето!).
,
используемым при построении множества
Парето!).
Пусть
во множестве
Паретозадачи (1) даны две точки
![]() ,
,
![]() и
значения всех частных
критериев оптимальностив них
и
значения всех частных
критериев оптимальностив них
![]() .
Введем меру относительного изменения
(снижения – знак "минус" или
повышения – знак "плюс") качества
решения по каждому из этих критериев
.
Введем меру относительного изменения
(снижения – знак "минус" или
повышения – знак "плюс") качества
решения по каждому из этих критериев
|
|
(2) |
где
![]() —
абсолютные изменения значений частных
критериев оптимальности
—
абсолютные изменения значений частных
критериев оптимальности
![]() при
переходе от решения
при
переходе от решения
![]() к
решению
к
решению
![]() .
Вычислим максимальное снижение качества
решения при переходе от решения
.
Вычислим максимальное снижение качества
решения при переходе от решения
![]() к
решению
к
решению
![]()
|
|
(3) |
Аналогично
вычислим максимальное повышение качества
решения при переходе от решения
![]() к
решению
к
решению
![]()
|
|
(4) |
Будем
говорить, что решение
![]() превосходит
решение
превосходит
решение
![]() ,
и писать
,
и писать
|
|
(5) |
С
другой стороны, будем говорить, что
решение
![]() превосходит
решение
превосходит
решение
![]() ,
и писать
,
и писать
|
|
(6) |
Пример 1
Пусть
заданы четыре частных
критерия оптимальности
![]() ,
,
![]() и
решения
и
решения
![]() принадлежащие
множеству
Паретозадачи (1). Положим, что критерии
принадлежащие
множеству
Паретозадачи (1). Положим, что критерии
![]() в
точках
в
точках
![]() имеют
следующие значения:
имеют
следующие значения:
Таблица 1
|
|
|
|
|
|
|
|
1 |
2 |
3 |
5 |
|
|
3 |
2 |
0 |
4 |
По формулам (2), (3), (4) последовательно имеем
![]()
![]()
![]()
![]()
![]()
![]()
Поскольку
![]() ,
т.е. максимальное относительное повышение
качества решения превышает максимальное
относительное снижение качества решения,
то решение
,
т.е. максимальное относительное повышение
качества решения превышает максимальное
относительное снижение качества решения,
то решение
![]() превосходит
решения
превосходит
решения
![]() :
:
![]() .
.
Таким
образом, дополнительной информацией в
методе
справедливого компромиссаявляется
информация об одинаковой важности всехчастных
критериев
![]() ,
а также информация о справедливом
компромиссе, формализованная отношением
превосходства
,
а также информация о справедливом
компромиссе, формализованная отношением
превосходства
![]() .
.
Упрощенная схема метода справедливого компромисса.
Рассмотрим основные этапы метода справедливого компромисса.
Полагаем счетчик числа итераций
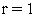 .
.Тем или иным способом выбираем из множества Паретозадачи
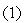 решение
решение
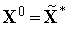 .
.Вычисляем значения всех частных критериев оптимальности
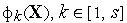 в
точке
в
точке
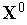 .
.Тем или иным способом выбираем из множества Паретозадачи (1) решение
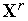 .
.Вычисляем значения всех частных критериев оптимальности
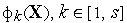 в
точке
в
точке
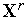 .
.По формулам (2), (3), (4), (5), (6) из числа решений
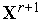 ,
,
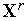 находим
превосходящее решение. Обозначим его
находим
превосходящее решение. Обозначим его
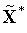 .
.Если условие окончания итераций выполнено (см. ниже), то принимаем точку
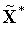 в
качестве приближенного решения задачи
(1) и заканчиваем вычисления. Иначе
полагаем
в
качестве приближенного решения задачи
(1) и заканчиваем вычисления. Иначе
полагаем
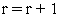 и
переходим к п.3
и
переходим к п.3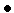
В простейшем случае выбор решений может быть произведен случайным образом. В качестве условия окончания итераций в этом случае может быть использовано достижение заданного количества итераций.
Выбор
решений
![]() может
быть произведен также с помощью полного
перебора узлов какой-либо сетки,
покрывающей множество
может
быть произведен также с помощью полного
перебора узлов какой-либо сетки,
покрывающей множество
![]() .
.
Поскольку метод справедливого компромиссаиспользует относительные изменениячастных критериев оптимальности, этот метод инвариантен к масштабу измерения частных критериев, т.е. не требуется их нормализация.
11.5 Метод приближения к идеальному решению для решения задач многокритериальной оптимизации
Рассмотрим задачу многокритериальной оптимизации
|
|
(1) |
где
![]() —
векторный
критерий оптимальности,
—
векторный
критерий оптимальности,
![]() —
частные
критерии оптимальности(скалярные),
—
частные
критерии оптимальности(скалярные),
![]() —
множество
допустимых значений вектора варьируемых
параметров.
—
множество
допустимых значений вектора варьируемых
параметров.
Метод приближения к идеальному решениюотносится к группе методов, основанных на сведениизадачи многокритериальной оптимизациик задаче однокритериальной оптимизации.
Идеальным
решением задачи многокритериальной
оптимизации(1) называется вектор
![]() ,
где
,
где
![]()
минимальное
значение частного
критерия оптимальности
![]() во
множестве
во
множестве
![]() .
.
Напомним,
что векторы
![]() ,
доставляющие минимумы соответствующим
критериям
оптимальности
,
доставляющие минимумы соответствующим
критериям
оптимальности
![]() ,
вообще говоря, различны.
,
вообще говоря, различны.
Введем в рассмотрение скалярный критерий оптимальности
|
|
(2) |
где
![]() —
некоторая векторная норма, например,
евклидова;
—
некоторая векторная норма, например,
евклидова;
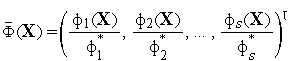 —
нормированный векторный
критерий оптимальности;
—
нормированный векторный
критерий оптимальности;
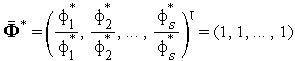 —
нормированное идеальное
решение(единичный
—
нормированное идеальное
решение(единичный
![]() -вектор).
-вектор).
В
методе
приближения к идеальному решениювместо задачи (1) решаетсязадача
условной оптимизациисо скалярнымкритерием
оптимальности
![]()
|
|
(3) |
Заметим,
что если
![]() —
евклидова норма, то критерий
оптимальности
—
евклидова норма, то критерий
оптимальности
![]() является
квадратичной функцией компонент вектора
является
квадратичной функцией компонент вектора
![]() .
Поэтому если, дополнительно, множество
.
Поэтому если, дополнительно, множество
![]() является
выпуклым, то задача (3) представляет
собой задачу
квадратичного программирования. Этот
факт значительно упрощает решение
задачи (3).
является
выпуклым, то задача (3) представляет
собой задачу
квадратичного программирования. Этот
факт значительно упрощает решение
задачи (3).
Дополнительной
информацией в методе
приближения к идеальному решениюявляется информация, заключенная в
способе сворачиваниявекторного
критерия оптимальности
![]() в
скалярный критерий
в
скалярный критерий
![]() .
.
Поскольку метод приближения к идеальному решениюиспользует нормированныечастные критерии оптимальности, этот метод инвариантен к масштабу измерения частных критериев.
11.6 Метод последовательных уступок для решения задач многокритериальной оптимизации
Рассмотрим задачу многокритериальной оптимизации
|
|
(1) |
где
![]() —
векторный
критерий оптимальности,
—
векторный
критерий оптимальности,
![]() —
частные
критерии оптимальности(скалярные),
—
частные
критерии оптимальности(скалярные),
![]() —
множество
допустимых значений вектора варьируемых
параметров.
—
множество
допустимых значений вектора варьируемых
параметров.
В
методе
последовательных уступокпрежде
производится качественный анализ
относительной важностичастных
критериев оптимальности
![]() .
На основании этого анализа частные
критерии располагаются и нумеруются в
порядке убывания важности. Положим, что
главным является критерий
.
На основании этого анализа частные
критерии располагаются и нумеруются в
порядке убывания важности. Положим, что
главным является критерий
![]() ,
следующим по важности – критерий
,
следующим по важности – критерий
![]() ,
затем следуют остальные частные критерии
,
затем следуют остальные частные критерии
![]() .
.
Затем
для каждого из частных
критериев, исключая последний по
важности критерий
![]() ,
назначаются уступки
,
назначаются уступки
![]() —
допустимые, с точки зрения лица,
принимающего решения (ЛПР), увеличения
соответствующих критериев
—
допустимые, с точки зрения лица,
принимающего решения (ЛПР), увеличения
соответствующих критериев
![]() относительно
их оптимальных значений фk(
относительно
их оптимальных значений фk(![]() )=
)=![]() =
=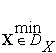 фk(
фk(![]() ).
).
Далее
решается задача минимизации критерия
![]()
|
|
(2) |
и
определяется множества
допустимых значений
![]() —
сужение множества допустимых значений:
—
сужение множества допустимых значений:
|
|
(3) |
Переходим
к следующему по важности критерию
![]() .
Решается задача минимизации критерия
.
Решается задача минимизации критерия
![]()
|
|
(4) |
и
определяется множества
допустимых значений
![]() —
сужение множества допустимых значений:
—
сужение множества допустимых значений:
|
|
(5) |
Т.е.
минимизация критерия
![]() производится
при условии, что значения предыдущего
критерия
производится
при условии, что значения предыдущего
критерия
![]() не
превосходит величины
не
превосходит величины
![]() .
.
И
т.д. до предпоследнего по важности
критерия
![]() .
Решается задача минимизации критерия
.
Решается задача минимизации критерия
![]()
|
|
(6) |
и
определяется множества
допустимых значений
![]() —
сужение множества допустимых значений:
—
сужение множества допустимых значений:
|
|
(7) |
Наконец,
переходим к последнему по важности
критерию
![]() .
Решается задача минимизации критерия
.
Решается задача минимизации критерия
![]()
|
|
(8) |
В
качестве решения задачи (1) принимается
решение
![]() со
значениями частных
критериев
со
значениями частных
критериев
![]() .
.
Достоинством метода последовательных уступокявляется то, что он легко позволяет контролировать, ценой какойуступкив одномчастном критерииприобретается выигрыш в другом частном критерии. Заметим также, что свобода выбора решения, приобретаемая ценой даже незначительных уступок, может оказаться существенной, так как в окрестностях минимума обычно эффективность решений меняется слабо.
Не смотря на идейную простоту метода последовательных уступок, практическое применение этого метода сопряжено со значительными трудностями.
Метод последовательных уступокприменим для решения лишь техзадач многокритериальной оптимизации, в которых всечастные критерииестественным образом упорядочены по степени важности.
Поскольку взаимосвязь частных критериевобычно неизвестна, заранее назначить величиныуступок
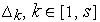 ,
как правило, не удается. Поэтому изучение
взаимосвязи частных критериев и
назначение величин уступки приходится
производить в процессе решения задачи.
Практически, для этого вначале оценивают
взаимосвязь частных критериев
,
как правило, не удается. Поэтому изучение
взаимосвязи частных критериев и
назначение величин уступки приходится
производить в процессе решения задачи.
Практически, для этого вначале оценивают
взаимосвязь частных критериев
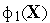 ,
,
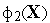 .
Для этого задают несколько величин
уступок
.
Для этого задают несколько величин
уступок
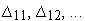 и
определяют соответствующие значения
второго по важности критерия
и
определяют соответствующие значения
второго по важности критерия
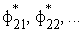 .
На основе анализа этой информации лицо,
принимающее решение, принимает решение
о величине первой уступки
.
На основе анализа этой информации лицо,
принимающее решение, принимает решение
о величине первой уступки
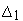 .
Затем аналогично оценивают взаимосвязь
частных критериев
.
Затем аналогично оценивают взаимосвязь
частных критериев
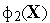 ,
,
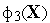 и
назначают величину второй уступки
и
назначают величину второй уступки
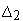 .
И так далее до критериев
.
И так далее до критериев
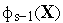 ,
,
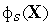 и
уступки
и
уступки
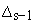 .
Таким образом, фактически приходится
решать каждую из задач (2), (4), (5), (6) не
однократно, как в изложенной схеме, а
многократно.
.
Таким образом, фактически приходится
решать каждую из задач (2), (4), (5), (6) не
однократно, как в изложенной схеме, а
многократно.Изложенная схема метода последовательных уступокпредполагает, что каждыйчастный критерий
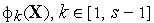 настолько
существенно более важен, чем последующий
частный критерий, что можно ограничиться
учетом только попарных связей критериев
и выбирать величину уступкидля данного критерия с учетом поведения
лишь одного следующего критерия.
настолько
существенно более важен, чем последующий
частный критерий, что можно ограничиться
учетом только попарных связей критериев
и выбирать величину уступкидля данного критерия с учетом поведения
лишь одного следующего критерия.Сложной самостоятельной проблемой является отыскание в явном виде множеств
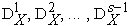 .
.
Дополнительной
информацией в методе
последовательных уступокявляется
информация об относительной важностичастных
критериев
![]() ,
а также информация об уступках
,
а также информация об уступках
![]() .
.