- •Глава 1. Математическая формулировка задачи непрерывной оптимизации в конечномерном пространстве
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения
- •Глава 12. Задачи оптимального управления и методы их приближенного решения
- •Глава 1. Математическая формулировка задачи оптимального проектирования.
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации.
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения.
- •Глава 4. Методы поиска локального минимума одномерных функций.
- •Глава 5. Методы поиска глобального минимума одномерных функций.
- •Глава 6. Многомерная локальная безусловная оптимизация. Детерминированные прямые методы.
- •Глава 7. Многомерная локальная безусловная оптимизация. Детерминированные методы первого и второго порядков.
- •1. Постановка задачи.
- •2. Итерационная формула.
- •Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска (прямые методы).
- •Глава 9. Многомерная локальная условная оптимизация.
- •Глава 10. Многомерная глобальная условная оптимизация.
- •Глава 11. Задачи многокритериальной оптимизации и методы их решения.
- •Глава 12. Задачи оптимального управления и методы их приближенного решения.
Глава 5. Методы поиска глобального минимума одномерных функций.
5.1 Метод перебора. Одномерный метод Монте-Карло
Некоторые методы решения многомерных задач оптимизациитребуют решения одномернойзадачи глобальной оптимизации(или совокупности таких задач).
Рассматривается
следующая одномерная задача
условной глобальной оптимизации):
найти минимум, вообще говоря,многоэкстремальной
функции
![]() (
(![]() ),
определенной в замкнутой области
допустимых значений
),
определенной в замкнутой области
допустимых значений
![]() ,
,
|
|
(1) |
Метод перебора
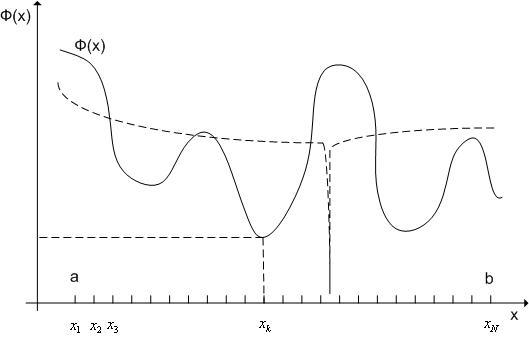
Схема метода перебора(см. рис. 1):
|
|
Рис. 1. К схеме метода перебора.
Покрываем интервал
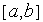 некоторой
сеткой с узлами
некоторой
сеткой с узлами
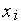 ,
,
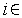 [1,
[1,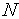 ].
].Производим испытаниев точке
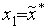 ,
т.е. вычисляем значения
,
т.е. вычисляем значения
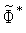 функции
функции
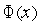 в
этой точке.
в
этой точке.Полагаем
 .
.Производим испытаниев точке
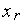 -
вычисляем значение
-
вычисляем значение
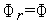 (
(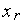 )
функции
)
функции
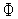 (
(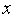 )
в этой точке.
)
в этой точке.Если
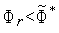 ,
то выполняем присваивания
,
то выполняем присваивания
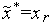 ,
,
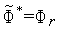 .
.Если
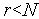 ,
то выполняем присваивание
,
то выполняем присваивание
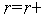 1
и переходим на п.4). Иначе - заканчиваем
вычисления.
1
и переходим на п.4). Иначе - заканчиваем
вычисления.Принимаем
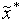 в
качестве приближенного значения точки
глобального минимума функции
в
качестве приближенного значения точки
глобального минимума функции
 (
(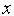 )
на интервале [
)
на интервале [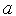 ,
,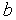 ]
или каким-либо из рассмотренных
одномерных методов
локальной оптимизацииорганизуем в
окрестности точки
]
или каким-либо из рассмотренных
одномерных методов
локальной оптимизацииорганизуем в
окрестности точки
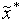 поиск
локального минимума этой функции
поиск
локального минимума этой функции
При
выборе количества узлов сетки
![]() ,
,
![]() [1,
[1,![]() ]
можно исходить из требуемой точности
решения
]
можно исходить из требуемой точности
решения
![]() –
максимальный шаг сетки принять равным
этой величине.
–
максимальный шаг сетки принять равным
этой величине.
Отметим, что метод перебора, как и любой другойметод глобальной оптимизации, при отсутствии априорной информации о свойствах минимизируемой функции не гарантирует нахождение глобального минимума (см. пунктирный график на рис. 1).
Одномерный метод Монте-Карло
Схема одномерного метода Монте-Карло:
Генерируем с помощью какого-либо программного генератора случайных чисел, равномерно распределенных в интервале [
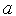 ,
,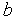 ],
случайное число
],
случайное число
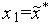 .
.Производим испытаниев точке
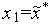 -
вычисляем значения
-
вычисляем значения
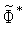 функции
функции
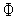 (
(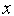 )
в этой точке.
)
в этой точке.Полагаем
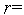 2.
2.Аналогично п. 1) генерируем случайное число
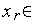 [
[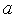 ,
,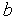 ]
.
]
.Производим испытаниев точке
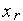 -
вычисляем значение
-
вычисляем значение
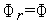 (
(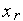 )
функции
)
функции
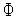 (
(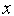 )
в этой точке.
)
в этой точке.Если
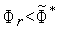 ,
то выполняем присваивания
,
то выполняем присваивания
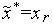 ,
,
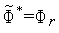 .
.Если
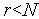 ,
то выполняем присваивание
,
то выполняем присваивание
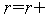 1
и переходим на п. 4). Иначе - заканчиваем
вычисления. Здесь
1
и переходим на п. 4). Иначе - заканчиваем
вычисления. Здесь
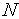 –
количество испытаний.
–
количество испытаний.Принимаем
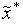 в
качестве приближенного значения точки
глобального минимума функции
в
качестве приближенного значения точки
глобального минимума функции
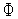 (
(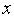 )
на интервале [
)
на интервале [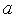 ,
,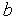 ]
или каким-либо из рассмотренных
одномерных методов
локальной оптимизацииорганизуем в
окрестности точки
]
или каким-либо из рассмотренных
одномерных методов
локальной оптимизацииорганизуем в
окрестности точки
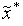 поиск
локального минимума этой функции
поиск
локального минимума этой функции
При
достаточно большом
![]() метода
гарантирует нахождение глобального
минимума с высокой вероятностью.
метода
гарантирует нахождение глобального
минимума с высокой вероятностью.
5.2 Метод выделения интервалов унимодальности
Рассмотрим
одномерную задачу
условной глобальной оптимизации):
найти минимум одномерноймногоэкстремальной
функции
![]() (
(![]() ),
определенной в замкнутой
области
допустимых значений
),
определенной в замкнутой
области
допустимых значений
![]() и
имеющей в этой области конечное число
минимумов,
и
имеющей в этой области конечное число
минимумов,
|
|
(1) |
Метод
выделения интервалов унимодальностифункции
![]() (
(![]() )
требует априорного знания оценки
)
требует априорного знания оценки
![]() 0
минимального расстояния между локальными
минимумами этой функции.
0
минимального расстояния между локальными
минимумами этой функции.
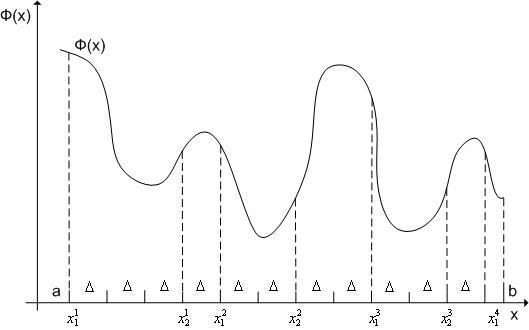
Схема метода (см. рис. 1):
|
|
Рис. 1. К схеме метода выделения интервалов унимодальности.
Полагаем
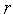 =1.
=1.Если функция
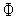 (
(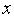 )
в точке
)
в точке
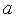 возрастает,
то полагаем
возрастает,
то полагаем
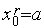 переходим
на п. 4).
переходим
на п. 4).Если функция
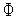 (
(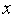 )
в точке
)
в точке
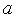 убывает,
то полагаем
убывает,
то полагаем
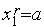 и
переходим на п. 5).
и
переходим на п. 5).Последовательно увеличивая
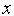 на
величину
на
величину
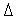 по
формуле
по
формуле
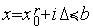 ,
,
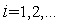 ,
находим первую точку
,
находим первую точку
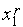 ,
в которой функция
,
в которой функция
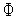 (
(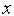 )
убывает. Здесь и далее
)
убывает. Здесь и далее
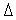 -
величина в несколько раз меньшая
величины
-
величина в несколько раз меньшая
величины
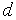 .
.Последовательно увеличивая
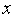 на
величину
на
величину
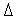 по
формуле
по
формуле
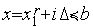 ,
,
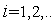 ,
находим первую точку
,
находим первую точку
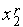 ,
в которой функция
,
в которой функция
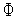 (
(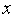 )
возрастает.
)
возрастает.В качестве
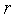 -го
интервала унимодальности принимаем
интервал [
-го
интервала унимодальности принимаем
интервал [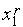 ,
, ].
].Если интервал [
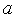 ,
,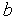 ]
исчерпан, переходим на п.8), иначе полагаем
]
исчерпан, переходим на п.8), иначе полагаем
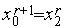 ,
,
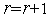 и
переходим на п.4).
и
переходим на п.4).Положим, что общее количество найденных интервалов унимодальности функции
 (
(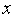 )
равно
)
равно
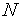 -1.
Каким-либо одномерным методом
локальной оптимизациинаходим
локальный минимум функции
-1.
Каким-либо одномерным методом
локальной оптимизациинаходим
локальный минимум функции
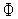 (
(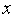 )
в каждом из
)
в каждом из
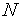 -1
интервалов унимодальности. Обозначим
точки этих минимумов
-1
интервалов унимодальности. Обозначим
точки этих минимумов
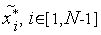 .
Соответствующие значения функции
.
Соответствующие значения функции
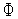 (
(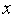 )
обозначим
)
обозначим
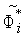 ,
,
 .
Добавим к точкам
.
Добавим к точкам
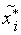 точки
точки
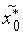 ,
,
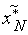 и
вычислим соответствующие значения
и
вычислим соответствующие значения
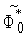 ,
,
 функции
функции
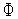 (
(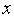 ).
).Найдем минимальную из величин
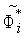 ,
,
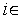 [0,
[0,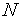 ]
и соответствующее значение аргумента:
]
и соответствующее значение аргумента:
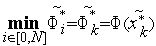 .
.В качестве решения задачи глобальной оптимизации(1) примем точку
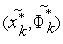
На
рис. 1 интервалами унимодальности
являются интервалы [![]() ,
,
![]() ],
[
],
[![]() ,
,
![]() ],
[
],
[![]() ,
,
![]() ].
].
Для
определения того, возрастает или убывает
в данной точке функция
![]() (
(![]() ),
может использоваться ее первая разность
в этой точке
),
может использоваться ее первая разность
в этой точке
![]() ,
где
,
где
![]() -
некоторая малая величина. А именно, если
-
некоторая малая величина. А именно, если
![]() >0,
то функция возрастает в точке
>0,
то функция возрастает в точке
![]() ;
иначе – убывает. Заметим, что при этом
в каждой точке требуется выполнить
дополнительное испытаниефункции
;
иначе – убывает. Заметим, что при этом
в каждой точке требуется выполнить
дополнительное испытаниефункции
![]() (
(![]() ).
).
Если
функция
![]() (
(![]() )
непрерывно дифференцируема в интервале
[
)
непрерывно дифференцируема в интервале
[![]() ,
,![]() ],
то для определения того, возрастает или
убывает в данной точке эта функция,
можно, очевидно, использовать значения
первой производной функции
],
то для определения того, возрастает или
убывает в данной точке эта функция,
можно, очевидно, использовать значения
первой производной функции
![]() (
(![]() )
в этой точке. А именно, если
)
в этой точке. А именно, если
![]() ,
то в точке
,
то в точке
![]() функция
функция
![]() (
(![]() )
возрастает; в противном случае – убывает.
)
возрастает; в противном случае – убывает.
Замечание
1.
Если априорная оценка
![]() минимального
расстояния между локальными минимумами
функции
минимального
расстояния между локальными минимумами
функции
![]() (
(![]() )
отсутствует, то никаких оснований
полагать, что в интервалах, выделенных
с помощью рассмотренного алгоритма,
функция
)
отсутствует, то никаких оснований
полагать, что в интервалах, выделенных
с помощью рассмотренного алгоритма,
функция
![]() (
(![]() )
является унимодальной
функцией. Пусть, например, функция
)
является унимодальной
функцией. Пусть, например, функция
![]() (
(![]() )
на интервале [
)
на интервале [![]() ,
,![]() ]
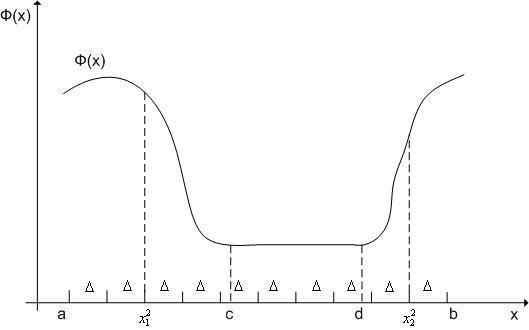
постоянна (см. рис. 2). Если к такой
функции применить алгоритм выделения
интервалов унимодальности с любым
]
постоянна (см. рис. 2). Если к такой
функции применить алгоритм выделения
интервалов унимодальности с любым
![]() >0,
то в качестве интервала унимодальности
будет выделен интервал
>0,
то в качестве интервала унимодальности
будет выделен интервал
![]() ,
на котором функция
,
на котором функция
![]() (
(![]() )
имеет бесконечное количество минимумов,
т.е. не является унимодальной
функцией
)
имеет бесконечное количество минимумов,
т.е. не является унимодальной
функцией
|
|
Рис. 2. К замечанию 1.
5.3 Метод аппроксимирующих моделей
Рассмотрим
одномерную задачу
условной глобальной оптимизации):
найти минимум одномерноймультимодальной
функции
![]() (
(![]() ),
определенной в замкнутой области
допустимых значений
),
определенной в замкнутой области
допустимых значений
![]() :
:
|
|
(1) |
Схема метода
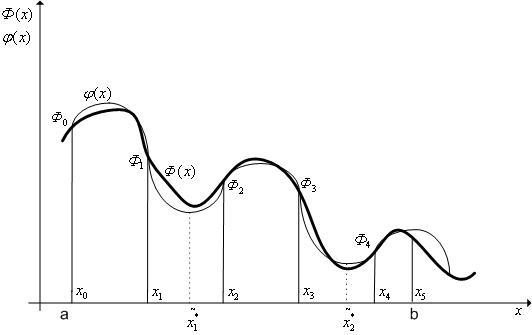
Схема метода аппроксимирующих моделей(см. рис. 1):
Покрываем интервал [
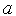 ,
,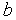 ]
некоторой сеткой с узлами
]
некоторой сеткой с узлами
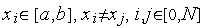 и
производим испытанияв точках
и
производим испытанияв точках
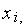
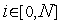 ,
т.е. вычисляем значения функции
,
т.е. вычисляем значения функции
 (
(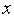 )
в этих точках
)
в этих точках
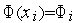 ,
,
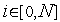 .
.Строим аппроксимирующую функцию
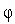 (
(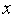 ),
проходящую через точки
),
проходящую через точки
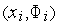 ,
,
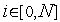 .
Эту функцию принято называть математической
моделью минимизируемой функции
.
Эту функцию принято называть математической
моделью минимизируемой функции
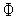 (
(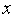 )
или модельной
функцией.
)
или модельной
функцией.Оцениваем адекватность построенной модели
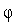 (
(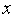 ).
Для этого:
).
Для этого:
производим дополнительные испытанияфункции
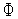 (
(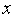 )
в некоторых точках
)
в некоторых точках
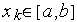 ,
,
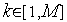 ;
;вычисляем значения модельной функции
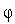 (
(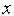 )
и функции
)
и функции
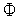 (
(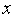 )
в этих точках
)
в этих точках
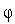 (
(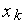 ),
),
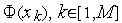 ;
;вычисляем погрешность аппроксимации, например,
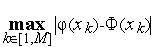 .
.
Если
погрешность аппроксимации превышает
заданную, то по результатам всех
предшествующих испытанийстроим новуюмодельную
функцию
![]() (
(![]() )
и переходим на п. 3).
)
и переходим на п. 3).
Определяем
положение глобального минимума модельной
функции
![]() (
(![]() ),
который или принимается в качестве
глобального минимума функции
),
который или принимается в качестве
глобального минимума функции
![]() (
(![]() ),
или уточняется с помощью какого-либо
метода
локальной оптимизации
),
или уточняется с помощью какого-либо
метода
локальной оптимизации![]()
|
|
Рис. 1. К схеме метода аппроксимирующих моделей. N=5;
На
рис. 1
![]() ,
,
![]() -
точки локального минимума модельной
функции
-
точки локального минимума модельной
функции
![]() (
(![]() );
точка
);
точка
![]() -
приближенное значение точки глобального
минимума функции
-
приближенное значение точки глобального
минимума функции
![]() (
(![]() )
на интервале
)
на интервале
![]() .
.
В
качестве модельных
функций
![]() (
(![]() )
чаще всего используют полиномы и сплайны.
)
чаще всего используют полиномы и сплайны.
Рассмотрим использование в качестве модельной функцииполиномов.
Аппроксимирующий полином Лагранжа
Будем искать аппроксимирующий полином в виде
|
|
(2) |
где
![]() (
(![]() ),
),
![]() -
неизвестные полиномы от
-
неизвестные полиномы от
![]() ,
независящие от аппроксимируемой функции
,
независящие от аппроксимируемой функции
![]() (
(![]() ).
).
Из
того условия, что модельная
функция
![]() (
(![]() )
должна совпадать с аппроксимируемой
функцией
)
должна совпадать с аппроксимируемой
функцией
![]() (
(![]() )
в узлах сетки
)
в узлах сетки
![]() ,
,
![]() [0,
[0,![]() ],
имеем систему из
],
имеем систему из
![]() равенств
равенств
|
|
(3) |
Для
выполнения равенств (3) полиномы
![]() ,
,
![]() ,
очевидно, должны удовлетворять условиям
,
очевидно, должны удовлетворять условиям
|
|
(4) |
или,
другими словами, полином
![]() (
(![]() ),
),
![]() должен
иметь в качестве корней все числа
должен
иметь в качестве корней все числа
![]() ,
,
![]() ,
кроме числа
,
кроме числа
![]() ,
а при
,
а при
![]() должен
иметь значение, равное единице.
должен
иметь значение, равное единице.
Условию
(4) удовлетворяют только полиномы вида
![]() ,
где
,
где
![]() –
неизвестная константа. Найдем эту
константу из условия
–
неизвестная константа. Найдем эту
константу из условия
![]() :
:
![]() ;
;
![]() .
.
Таким образом,
|
|
(5) |
и искомый аппроксимирующий полином определяют выражением
|
|
(6) |
Полином (6) называется аппроксимирующим полиномом Лагранжа.
Использование
аппроксимирующего полинома Лагранжа
(6) в качестве модельной
функцииидейно очень просто, но
обладает существенным недостатком.
Пусть после построения этого полинома
на сетке
![]() ,
,
![]() [0,
[0,![]() ]
и проверке его адекватности выясняется,
что погрешность аппроксимации превышает
заданную. Тогда, в соответствии с
рассмотренной выше схемой метода,
необходимо построить новый полином
Лагранжа на сетке, полученной объединением
сеток
]
и проверке его адекватности выясняется,
что погрешность аппроксимации превышает
заданную. Тогда, в соответствии с
рассмотренной выше схемой метода,
необходимо построить новый полином
Лагранжа на сетке, полученной объединением
сеток
![]() ,
,
![]() ,
что требует пересчета всех посчитанных
ранее функций
,
что требует пересчета всех посчитанных
ранее функций
![]() ,
,
![]() .
От этого недостатка свободна модификация
аппроксимирующего полинома Лагранжа
– аппроксимирующий полином Ньютона.
.
От этого недостатка свободна модификация
аппроксимирующего полинома Лагранжа
– аппроксимирующий полином Ньютона.
Нахождение стационарных точек аппроксимирующего полинома.
После
построения аппроксимирующего полинома
возникает задача нахождения стационарных
точек функции
![]() (
(![]() )
(см. схему метода). Поскольку аппроксимирующий
полином непрерывен и, по крайней мере,
один раз непрерывно дифференцируем,
его стационарные точки удобно искать
как нули первой производной – т.е. как
корни уравнения
)
(см. схему метода). Поскольку аппроксимирующий
полином непрерывен и, по крайней мере,
один раз непрерывно дифференцируем,
его стационарные точки удобно искать
как нули первой производной – т.е. как
корни уравнения
|
|
(7) |
Для
поиска корней уравнения чаще всего
используют метод хорд и метод касательных,
использующие линейную интерполяцию
функции
![]() (
(![]() )
(см. параграф 4.8), а также другие методы.
)
(см. параграф 4.8), а также другие методы.