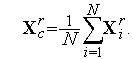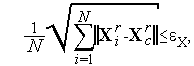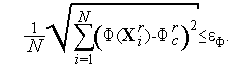- •Глава 1. Математическая формулировка задачи непрерывной оптимизации в конечномерном пространстве
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения
- •Глава 12. Задачи оптимального управления и методы их приближенного решения
- •Глава 1. Математическая формулировка задачи оптимального проектирования.
- •Глава 2. Условия существования минимума в детерминированных задачах оптимизации.
- •Глава 3. Классификация поисковых методов оптимизации и методология их сравнения.
- •Глава 4. Методы поиска локального минимума одномерных функций.
- •Глава 5. Методы поиска глобального минимума одномерных функций.
- •Глава 6. Многомерная локальная безусловная оптимизация. Детерминированные прямые методы.
- •Глава 7. Многомерная локальная безусловная оптимизация. Детерминированные методы первого и второго порядков.
- •1. Постановка задачи.
- •2. Итерационная формула.
- •Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска (прямые методы).
- •Глава 9. Многомерная локальная условная оптимизация.
- •Глава 10. Многомерная глобальная условная оптимизация.
- •Глава 11. Задачи многокритериальной оптимизации и методы их решения.
- •Глава 12. Задачи оптимального управления и методы их приближенного решения.
Глава 8. Многомерная локальная безусловная оптимизация. Методы случайного поиска (прямые методы).
8.1 Метод с возвратом при неудачном шаге. Метод наилучшей пробы
Рассматривается
следующая многомерная задача
локальной безусловной оптимизации:
найти минимумкритерия
оптимальности
![]() (
(![]() ),
определенного в
),
определенного в
![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве
![]() ,
,
|
|
(1) |
При решении задачи (1) методом с возвратом при неудачном шаге(одношаговый метод оптимизации) используется итерационная формула
|
|
(2) |
где
![]() -
величина шага на
-
величина шага на
![]() -ой
итерации,
-ой
итерации,
![]() -
реализация
-
реализация
![]() -мерного
случайного вектора,
-мерного
случайного вектора,
![]() -
некоторая векторная норма. Обычно в
качестве координат вектора
-
некоторая векторная норма. Обычно в
качестве координат вектора
![]() используют
независимые случайные величины,
равномерно распределенные в интервале
используют
независимые случайные величины,
равномерно распределенные в интервале
![]() .
.
Схема метода с возвратом при неудачном шаге.
Задаем начальную точку
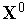 ,
начальную длину шага
,
начальную длину шага
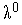 и
полагаем счетчик числа итераций
и
полагаем счетчик числа итераций
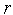 =0.
=0.Задаем начальное значение счетчика числа неудачных попыток
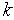 =1.
=1.Получаем реализацию случайных чисел
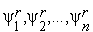 -
компонент вектора
-
компонент вектора
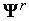 и
по формуле (2) находим пробную точку
и
по формуле (2) находим пробную точку
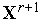 .
.Вычисляем значение
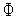 (
(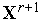 )
функции
)
функции
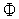 (
(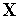 )
в точке
)
в точке
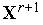 .
.Если
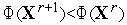 ,
то полагаем
,
то полагаем
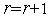 и
переходим к п.3. Иначе – переходим к
п.6.
и
переходим к п.3. Иначе – переходим к
п.6.Полагаем
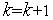 .
Если
.
Если
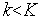 ,
то переходим к п.3. Иначе – переходим к
п.7. Здесь
,
то переходим к п.3. Иначе – переходим к
п.7. Здесь
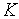 –
предельное количество неудачных попыток
(свободный параметр метода). Рекомендуется
–
предельное количество неудачных попыток
(свободный параметр метода). Рекомендуется
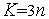 .
.Проверяем условие окончания поиска (см. ниже). Если условие окончания поиска выполнено, то полагаем
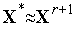 и
завершаем итерации. Иначе – полагаем
и
завершаем итерации. Иначе – полагаем
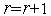 ,
,
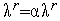 и
переходим к п. 2. Здесь
и
переходим к п. 2. Здесь
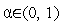 -
коэффициент уменьшения шага (свободный
параметр метода)
-
коэффициент уменьшения шага (свободный
параметр метода)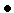
В качестве условия окончания поиска можно использоваться одно из стандартных условий окончания итераций:
|
|
(3) |
где
![]() -
константа, определяющая требуемую
точность решения по
-
константа, определяющая требуемую
точность решения по
![]() ;
;
|
|
(4) |
где
![]() -
константа, определяющая требуемую
точность решения по
-
константа, определяющая требуемую
точность решения по
![]() .
.
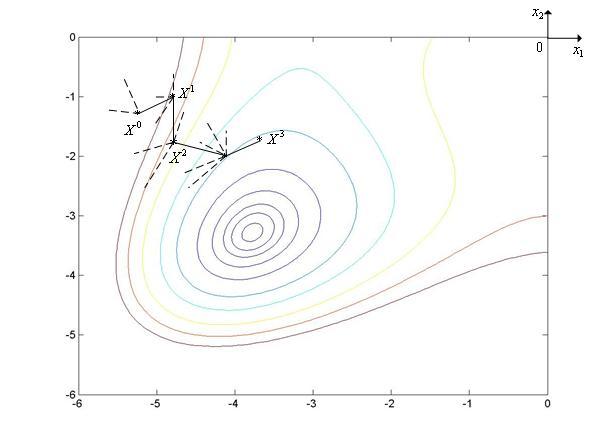
Метод с возвратом при неудачном шагеиллюстрирует рис. 1, на котором показан фрагмент линий уровняфункции Химмельблау.
|
|
Рис. 1. Траектория поиска минимума функции Химмельблау методом с возвратом при неудачном шаге. Пунктиром на рисунке показаны неудачные шаги.
Модификацией метода с возвратом при неудачном шагеявляетсяметод наилучшей пробы(такжеодношаговый метод оптимизации).
Схема метода наилучшей пробы.
Задаем начальную точку
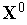 ,
начальную длину шага
,
начальную длину шага
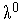 и
полагаем счетчик числа итераций
и
полагаем счетчик числа итераций
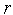 =0.
=0.Генерируем
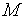 случайных
векторов
случайных
векторов
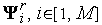 и
по формуле (2) находим пробные точки
и
по формуле (2) находим пробные точки
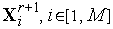
Вычисляем значения
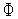 (
(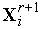 )
функции
)
функции
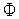 (
(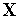 )
в пробных точках
)
в пробных точках
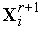 ,
,
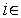 [1,
[1,
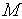 ]
и находим минимальное из этих значений
]
и находим минимальное из этих значений
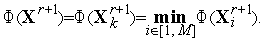
Если
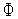 (
(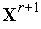 )<
)<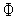 (
(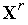 ),
то полагаем
),
то полагаем
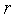 =
=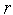 +1
и переходим к п.2. Иначе – переходим к
п.5.
+1
и переходим к п.2. Иначе – переходим к
п.5.Проверяем условие окончания поиска (см. (3), (4)). Если условие окончания поиска выполнено, то полагаем
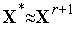 и
завершаем итерации. Иначе – полагаем
и
завершаем итерации. Иначе – полагаем
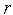 =
=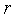 +1,
+1,
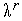 =
=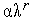 и переходим к п.2. Здесь
и переходим к п.2. Здесь
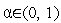 -
коэффициент уменьшения шага (свободный
параметр метода)
-
коэффициент уменьшения шага (свободный
параметр метода)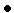
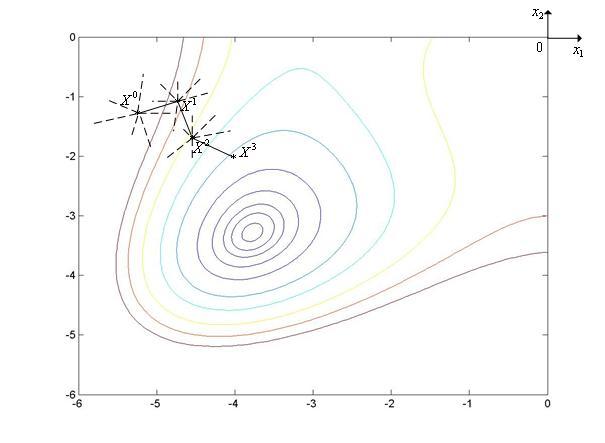
Метод наилучшей пробыиллюстрирует рис. 2, на котором показан фрагмент линий уровняфункции Химмельблау.
|
|
Рис. 2. Траектория поиска минимума функции Химмельблау методом наилучшей пробы. Пунктиром на рисунке показаны неудачные пробы.
8.2 Метод комплексов
Рассматривается
следующая многомерная задача
локальной безусловной оптимизации:
найти минимумкритерия
оптимальности
![]() (
(![]() ),
определенного в
),
определенного в
![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве
![]() ,
,
|
|
(1) |
Комплексомназывается многогранник с
![]() вершинами
(не обязательно выпуклый). Рекомендуется
вершинами
(не обязательно выпуклый). Рекомендуется
![]() .
Вообще говоря, комплексом в комбинаторной
топологии называется геометрическая
фигура, которая может быть разбита на
более элементарные фигуры. В нашем
случае такими элементарными фигурами
являются симплексы. Поэтому, говоря
более строго, в данном параграфе
рассматриваются симплициальные
комплексы.
.
Вообще говоря, комплексом в комбинаторной
топологии называется геометрическая
фигура, которая может быть разбита на
более элементарные фигуры. В нашем
случае такими элементарными фигурами
являются симплексы. Поэтому, говоря
более строго, в данном параграфе
рассматриваются симплициальные
комплексы.
При решении задачи (1) методом комплексов используются следующие операции:
генерация случайного комплекса;
отражение вершины комплекса с растяжением;
сжатие комплекса.
Генерация
случайного комплекса.
В пространстве
![]() координаты
вершин случайного комплекса с
координаты
вершин случайного комплекса с
![]() вершинами
могут быть найдены по формуле
вершинами
могут быть найдены по формуле
|
|
(2) |
где
![]() -
произвольная начальная точка,
-
произвольная начальная точка,
![]() –
номер вершины комплекса,
–
номер вершины комплекса,
![]() -
скаляр, определяющий размеры комплекса,
-
скаляр, определяющий размеры комплекса,
![]() -
реализация
-
реализация
![]() -мерного
случайного вектора,
-мерного
случайного вектора,
![]() -
некоторая векторная норма. Обычно в
качестве координат вектора
-
некоторая векторная норма. Обычно в
качестве координат вектора
![]() используют
независимые случайные величины,
равномерно распределенные в интервале
используют
независимые случайные величины,
равномерно распределенные в интервале
![]()
![]()
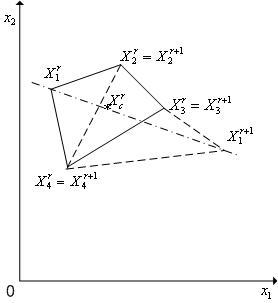
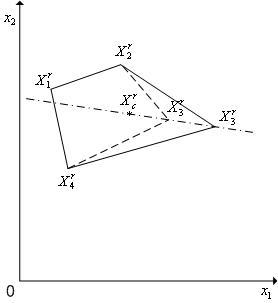
Отражение
вершины комплекса с растяжением.
Положим, что в пространстве
![]() тем
или иным способом задан комплекс
тем
или иным способом задан комплекс
![]() с
с
![]() вершинами
вершинами
![]() ,
и его вершину
,
и его вершину
![]() необходимо
отразить через
центр тяжести комплекса
с растяжением. В новом комплексе
необходимо
отразить через
центр тяжести комплекса
с растяжением. В новом комплексе
![]() все
вершины, кроме
все
вершины, кроме
![]() -ой,
совпадают с соответствующими вершинами
исходного комплекса
-ой,
совпадают с соответствующими вершинами
исходного комплекса
![]() ,
а
,
а
![]() -я
вершина находится на прямой, проходящей
через центр тяжести этого комплекса и
его вершину
-я
вершина находится на прямой, проходящей
через центр тяжести этого комплекса и
его вершину
![]() (см.
рис. 1). Обозначим координаты вершин
нового комплекса
(см.
рис. 1). Обозначим координаты вершин
нового комплекса
![]() .
Тогда имеем
.
Тогда имеем
|
|
(3) |
где
![]() -
коэффициент растяжения комплекса(рекомендуемое значение -
-
коэффициент растяжения комплекса(рекомендуемое значение -
![]() ),
),
![]() -
вектор координат центра тяжести комплекса
-
вектор координат центра тяжести комплекса
![]() :
:
|
|
(4) |
|
|
Рис. 1. Отражение вершины X1r комплекса Cr через центр его тяжести с растяжением. Пунктиром показан новый комплекс Cr+1.
Сжатие
комплекса. Положим, что в пространстве
![]() тем
или иным способом задан комплекс
тем
или иным способом задан комплекс
![]() с
с
![]() вершинами
вершинами
![]() ,
и его вершину
,
и его вершину
![]() необходимо
переместить ближе к центру тяжести
комплекса
необходимо
переместить ближе к центру тяжести
комплекса
![]() -
выполнить сжатие комплекса. В новом
комплексе
-
выполнить сжатие комплекса. В новом
комплексе
![]() все
вершины, кроме
все
вершины, кроме
![]() -ой,
совпадают с соответствующими вершинами
исходного комплекса
-ой,
совпадают с соответствующими вершинами
исходного комплекса
![]() ,
а
,
а
![]() -я
вершина находится на прямой, проходящей
через центр тяжести этого комплекса и
его вершину
-я
вершина находится на прямой, проходящей
через центр тяжести этого комплекса и
его вершину
![]() (см.
рис. 2). Обозначим координаты вершин
нового комплекса
(см.
рис. 2). Обозначим координаты вершин
нового комплекса
![]() ,
,
![]() [1,
[1,
![]() ].
Тогда имеем
].
Тогда имеем
|
|
(5) |
где
![]() -
коэффициент сжатия
комплекса(рекомендуемое значение -
2),
-
коэффициент сжатия
комплекса(рекомендуемое значение -
2),
![]() -
вектор координат центра тяжести комплекса
-
вектор координат центра тяжести комплекса
![]() (см.
(4)).
(см.
(4)).
|
|
Рис. 2. Сжатие комплекса Cr Пунктиром показан новый комплекс Cr.
Схема простейшего варианта метода комплексов.
Задаем начальную точку
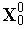 ,
исходя из которой должен быть построен
комплекс
,
исходя из которой должен быть построен
комплекс
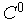 ,
начальное значение величины
,
начальное значение величины
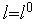 и
полагаем счетчик числа итераций
и
полагаем счетчик числа итераций
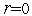 .
.Генерируем
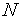 случайных
векторов
случайных
векторов
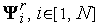 и
по формуле (2) находим координаты
и
по формуле (2) находим координаты
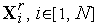 вершин
комплекса
вершин
комплекса
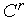 .
.Вычисляем значения
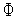 (
(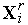 )
функции
)
функции
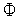 (
(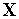 )
во всех вершинах комплекса
)
во всех вершинах комплекса
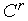 .
.Находим максимальное из значений функции
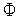 (
(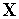 )
в вершинах комплекса
)
в вершинах комплекса
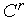

По формулам (3), (4) для комплекса
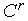 выполняем
отражение
вершины комплекса с растяжением
выполняем
отражение
вершины комплекса с растяжением
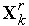 -
получаем вершину
-
получаем вершину
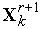 и
новый комплекс
и
новый комплекс
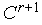 .
.Вычисляем значение
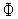 (
(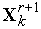 )
функции
)
функции
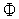 (
(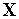 )
в вершине
)
в вершине
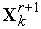 .
.Если
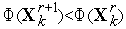 ,
то полагаем
,
то полагаем
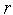 =
=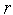 +1
и переходим к п.8. Иначе – по формулам
(5), (4) выполняем сжатие
симплекса
+1
и переходим к п.8. Иначе – по формулам
(5), (4) выполняем сжатие
симплекса
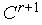 в
направлении
в
направлении
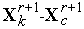 ,
полагаем
,
полагаем
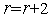 и
переходим к п.6.
и
переходим к п.6.Проверяем условие окончания поиска (см. ниже). Если условие окончания поиска выполнено, то в качестве точки
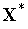 полагаем
вершину комплекса
полагаем
вершину комплекса
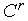 ,
к которой функция
,
к которой функция
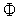 (
(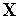 )
имеет наименьшее значение и завершаем
итерации. Иначе – переходим к п. 4
)
имеет наименьшее значение и завершаем
итерации. Иначе – переходим к п. 4
В
качестве критерия окончания поиска
может использоваться следующее условие:
максимальная длина ребра комплекса
![]() не
превышает
не
превышает
![]() -
требуемую точность решения по
-
требуемую точность решения по
![]() .
Может использоваться также следующее
аналогичное условие: максимальная
разность значений функции
.
Может использоваться также следующее
аналогичное условие: максимальная
разность значений функции
![]() (
(![]() )
в двух вершинах комплекса
)
в двух вершинах комплекса
![]() не
превышает
не
превышает
![]() -
требуемую точность решения по
-
требуемую точность решения по
![]() .
.
Могут использоваться также более сложные условия окончания поиска
|
|
(6) |
|
|
(7) |
В
формуле (6) векторная норма означает
расстояние вершины
![]() до
центра тяжести комплекса
до
центра тяжести комплекса
![]() ,
а сама формула (6) определяет среднее
расстояние вершин комплекса
,
а сама формула (6) определяет среднее
расстояние вершин комплекса
![]() до
его цента тяжести.
до
его цента тяжести.
В
формуле (7)
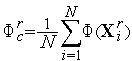 есть
среднее значение функции
есть
среднее значение функции
![]() (
(![]() )
в вершинах комплекса
)
в вершинах комплекса
![]() ,
а сама формула (7) определяет среднее
отклонение значений функции
,
а сама формула (7) определяет среднее
отклонение значений функции
![]() (
(![]() )
в вершинах комплекса
)
в вершинах комплекса
![]() от
этого среднего значения.
от
этого среднего значения.
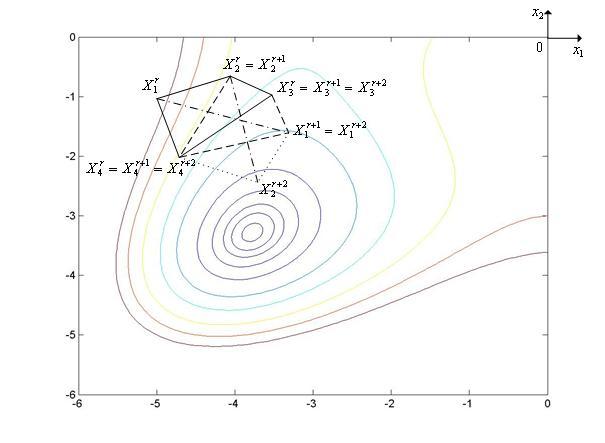
Метод
комплексовиллюстрирует рис. 3, на
котором показан фрагмент линий уровняфункции
Химмельблау. На рисунке исходныйкомплекс
![]() имеет
вершины
имеет
вершины
![]() ,
,
![]() [1,
4]. После отражения с растяжением вершины
[1,
4]. После отражения с растяжением вершины
![]() этого
комплекса, в которой функция имеет
максимальное значение, получаем комплекс
этого
комплекса, в которой функция имеет
максимальное значение, получаем комплекс
![]() с
вершинами
с
вершинами
![]() ,
,
![]() [1,
4]. После отражения с растяжением вершины
[1,
4]. После отражения с растяжением вершины
![]() комплекса
комплекса
![]() ,
в которой функция имеет максимальное
значение, получаем комплекс
,
в которой функция имеет максимальное
значение, получаем комплекс
![]() с
вершинами
с
вершинами
![]() ,
,
![]() [1,
4].
[1,
4].
|
|
Рис. 3. Траектория поиска минимума функции Химмельблау методом комплексов.
Известно множество модификаций рассмотренного метода комплексов, направленных, в частности, на преодоление «уплощения»комплексав процессе поиска. С этой целью через фиксированное количество итераций находятся максимальная и минимальная диагонали комплекса и, если их отношение превышает заданное, то по рассмотренной схеме производится построение нового комплекса.
8.3 Метод повторяющегося случайного поиска
Рассматривается
следующая многомерная задача
локальной безусловной оптимизации:
найти минимумкритерия
оптимальности
![]() (
(![]() ),
определенного в
),
определенного в
![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве
![]() ,
,
|
|
(1) |
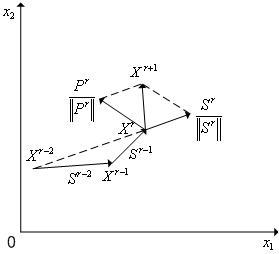
В методе повторяющегося случайного поиска(трех-шаговый метод) используется итерационная схема (см. рис. 1)
|
|
(2) |
где
![]() -
величина шага (скаляр) на
-
величина шага (скаляр) на
![]() -ой
итерации,
-ой
итерации,
![]() -
(
-
(![]() *1)-вектор,
определяющий направление шага на
*1)-вектор,
определяющий направление шага на
![]() -ой
итерации:
-ой
итерации:
|
|
(3) |
Здесь
![]() -
вектор «предыстории», определяющий
среднее направление поиска на двух
предыдущих шагах;
-
вектор «предыстории», определяющий
среднее направление поиска на двух
предыдущих шагах;
![]() -
некоторая векторная норма;
-
некоторая векторная норма;
![]() -
-
![]() -мерный
вектор псевдослучайных чисел, равномерно
распределенных в интервале
-мерный
вектор псевдослучайных чисел, равномерно
распределенных в интервале
![]() ;
скаляр
;
скаляр
![]() -
коэффициент, задающий относительные
веса детерминированной и случайной
компонент в векторе
-
коэффициент, задающий относительные
веса детерминированной и случайной
компонент в векторе
![]() (свободный
параметр метода); скаляр
(свободный
параметр метода); скаляр
![]() -
коэффициент, задающий относительные
веса векторов
-
коэффициент, задающий относительные
веса векторов
![]() в
векторе
в
векторе
![]() (свободный
параметр метода).
(свободный
параметр метода).
Заметим,
что отношение
![]() представляет
собой единичный вектор направления
представляет
собой единичный вектор направления
![]() ,
а отношение
,
а отношение
![]() -
единичный вектор направления
-
единичный вектор направления
![]() .
.
|
|
Рис. 1. К итерационной схеме метода повторяющегося случайного поиска.
Принято
![]() ,
,
![]() ,
,
![]() ,
так что
,
так что
![]() и
и
![]() .
.
Упрощенная схема метода повторяющегося случайного поиска.
Задаем начальную точку
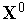 ,
начальный шаг
,
начальный шаг
 ,
значения коэффициентов
,
значения коэффициентов
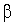 ,
,
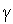 и
полагаем счетчик числа итераций
и
полагаем счетчик числа итераций
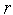 =2.
=2.Тем или иным способом, например, с помощью одношагового метода наилучшей пробыопределяем точки
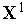 ,
,
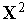 -
этап «разгона» метода.
-
этап «разгона» метода.Генерируем
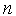 -мерный
случайный вектор
-мерный
случайный вектор
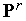 и
по формулам (2), (3) вычисляем координаты
точки
и
по формулам (2), (3) вычисляем координаты
точки
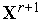 и
значение
и
значение
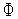 (
(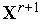 )
функции
)
функции
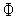 (
(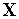 )
в этой точке.
)
в этой точке.Если
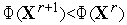 ,
то проверяем условие окончания итераций
(см. ниже). Если условие окончания
выполнено, то полагаем
,
то проверяем условие окончания итераций
(см. ниже). Если условие окончания
выполнено, то полагаем
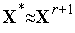 и
завершаем итерации. Если условие
окончания итераций не выполнено, то
некоторому правилу увеличиваем длину
шага
и
завершаем итерации. Если условие
окончания итераций не выполнено, то
некоторому правилу увеличиваем длину
шага
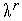 ,
например, полагая
,
например, полагая
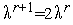 ,
принимаем
,
принимаем
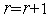 и
переходим к п.3. Если
и
переходим к п.3. Если
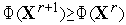 ,
то переходим к п. 5.
,
то переходим к п. 5.Некоторое фиксированное количество раз делаем попытку, исходя из той же точки
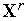 ,
не меняя длины шага
,
не меняя длины шага
 ,
добиться уменьшения значения функции
,
добиться уменьшения значения функции
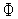 (
(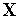 )
путем только изменения вектора
)
путем только изменения вектора
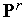 ,
т.е., не меняя
,
т.е., не меняя
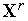 и
и
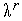 ,
переходим на п. 3. Если это фиксированное
количество попыток не привело к успеху,
то, исходя из той же точки
,
переходим на п. 3. Если это фиксированное
количество попыток не привело к успеху,
то, исходя из той же точки
 ,по
некоторому правилу уменьшаем длину
шага
,по
некоторому правилу уменьшаем длину
шага
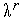 ,
например, полагая
,
например, полагая
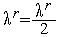 ,
и переходим к п.3
,
и переходим к п.3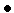
В качестве условия окончания поиска можно использоваться одно из стандартных условий окончания итераций
![]()
где
![]() -
константа, определяющая требуемую
точность решения по
-
константа, определяющая требуемую
точность решения по
![]() ;
;
![]()
где
![]() -
константа, определяющая требуемую
точность решения по
-
константа, определяющая требуемую
точность решения по
![]() .
.
Известно
множество модификаций рассмотренной
простейшей схемы метода
повторяющегося случайного поиска.
Например, в процессе поиска могут
изменяться по некоторым правилам не
только длина шага
![]() ,
но и коэффициенты
,
но и коэффициенты
![]() ,
,
![]() .
.
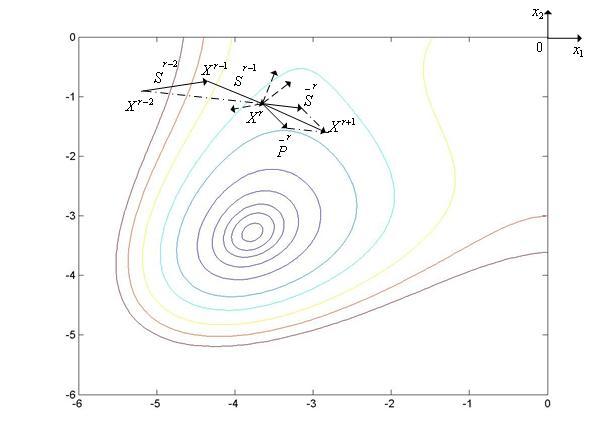
Метод повторяющегося случайного поискаиллюстрирует рис. 2, на котором показан фрагмент линий уровняфункции Химмельблау.
|
|
Рис. 2. Траектория поиска минимума функции Химмельблау методом повторяющегося случайного поиска.
На
рисунке принято
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
так что
,
так что
![]() и
и
![]() .
Пунктиром показаны отвергнутые векторы
.
Пунктиром показаны отвергнутые векторы
![]() .
.
8.4 Метод случайного поиска с постоянным радиусом поиска и случайными направлениями
Рассматривается
следующая многомерная задача
локальной безусловной оптимизации:
найти минимумкритерия
оптимальности
![]() (
(![]() ),
определенного в
),
определенного в
![]() -мерном
евклидовом пространстве
-мерном
евклидовом пространстве
![]() ,
,
|
|
(1) |
Метод
случайного поиска с постоянным радиусом
поиска и случайными направлениямииспользует процедуру генерации случайных
точек, равномерно распределенных по
поверхности гиперсферы в пространстве
![]() .
Пусть
.
Пусть
![]() -
вектор координат центра гиперсферы,
-
вектор координат центра гиперсферы,
![]() -
радиус гиперсферы,
-
радиус гиперсферы,
![]() -
вектор с началом в точке
-
вектор с началом в точке
![]() и
концом в искомой точке на поверхности
гиперсферы,
и
концом в искомой точке на поверхности
гиперсферы,
![]() -
углы между вектором
-
углы между вектором
![]() и
ортами координатных осей
и
ортами координатных осей
![]() .
.
Во
введенных обозначениях схема алгоритма
генерации случайных точек, равномерно
распределенных по поверхности гиперсферы
радиуса
![]() ,
может быть представлена в следующем
виде:
,
может быть представлена в следующем
виде:
генерируем
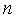 случайных
чисел, равномерно распределенных в
интервале
случайных
чисел, равномерно распределенных в
интервале
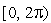 ;
;вычисляем направляющие косинусы
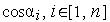 вектора
вектора
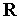 ;
;находим координаты искомой точки
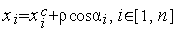 .
.
Упрощенная схема метода случайного поиска с постоянным радиусом поиска и случайными направлениями.
Задаем начальную точку
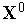 ,
начальный радиус гиперсферы
,
начальный радиус гиперсферы
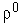 ,
и полагаем счетчик числа итераций
,
и полагаем счетчик числа итераций
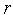 =0.
=0.Генерируем случайные точки
 ,
,
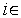 [1,
[1,
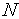 ]
равномерно распределенные по поверхности
гиперсферы радиуса
]
равномерно распределенные по поверхности
гиперсферы радиуса
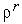 с
центром в точке
с
центром в точке
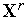 .
Здесь
.
Здесь
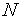 –
количество точек – свободный параметр
метода.
–
количество точек – свободный параметр
метода.Вычисляем значения минимизируемой функции
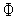 (
(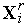 )
в полученных точках и находим точку, в
которой достигается минимальное
значение функции
)
в полученных точках и находим точку, в
которой достигается минимальное
значение функции
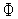 (
(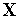 ):
):

Каким-либо из рассмотренных в главе 4 одномерных методов оптимизации(например,методом Паулла) находим минимум функции
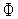 (
(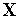 )
в направлении
)
в направлении
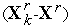 :
:
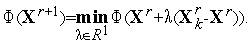
Проверяем условие окончания итераций (см. ниже). Если условие окончания выполнено, то полагаем
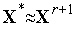 и
завершаем итерации. Иначе - принимаем
и
завершаем итерации. Иначе - принимаем
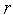 =
=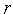 +1
и переходим к п.2
+1
и переходим к п.2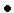
В качестве условия окончания поиска можно использоваться одно из стандартных условий окончания итераций:
![]()
где
![]() -
константа, определяющая требуемую
точность решения по
-
константа, определяющая требуемую
точность решения по
![]() ;
;
![]()
где
![]() -
константа, определяющая требуемую
точность решения по
-
константа, определяющая требуемую
точность решения по
![]() .
.
Могут
быть использованы также другие критерии
окончания поиска, например, условие не
превышения текущим радиусом гиперсферы
величины
![]() :
:
![]()
В
процессе поиска радиус гиперсферы может
меняться, увеличиваясь при удачных
шагах (вдали от точки
![]() )
и уменьшаясь при неудачных шагах (вблизи
от точки
)
и уменьшаясь при неудачных шагах (вблизи
от точки
![]() ).
).
Поиск может быть ускорен, если точки на гиперсфере выбирать (случайным образом) в некотором секторе по отношению к предыдущему направлению. Угол раскрыва этого сектора может меняться в процессе поиска.
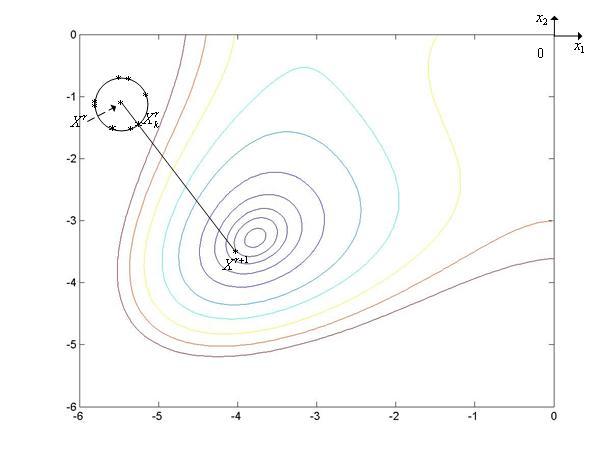
Метод случайного поиска с постоянным радиусом поиска и случайными направлениямииллюстрирует рис. 1, на котором показан фрагмент линий уровняфункции Химмельблау.
|
|
Рис. 1. Траектория поиска минимума функции Химмельблау методом случайного поиска с постоянным радиусом поиска и случайными направлениями (n=2).
На
рисунке точки, лежащие на окружности с
центром в точке
![]() ,
соответствуют случайным точкам
,
соответствуют случайным точкам
![]() ,
,
![]() [1,
[1,
![]() ].
].
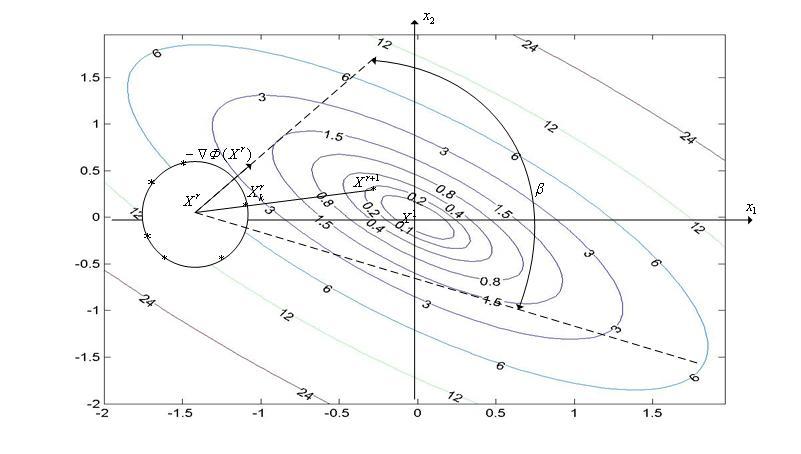
Примечание 1
Одна итерация по методу случайного поиска с постоянным радиусом поиска и случайными направлениямиможет привести к уменьшению минимизируемой функции в большей степени, чем один шаг поиска в направлении антиградиента этой функции. Данное утверждение иллюстрирует рис. 2, на котором показаны лини уровня двумерной квадратичной функции
![]()
(см. параграф 6.4).
|
|
Рис. 2. Один шаг поиска в направлении антиградиента минимизируемой функции (∇Φ(Xr)) приводит на линию уровня (1.5). В то же время одна итерация по методу случайного поиска с постоянным радиусом поиска и случайными направлениями – на линию уровня ~0.2. Точки на окружности с центром в точке Xr соответствуют случайным точкам. Любое направление поиска в секторе β лучше, чем направление антиградиента.