Разложения функции

Функция, определенная при , разлагается по полиномам Чебышева

,

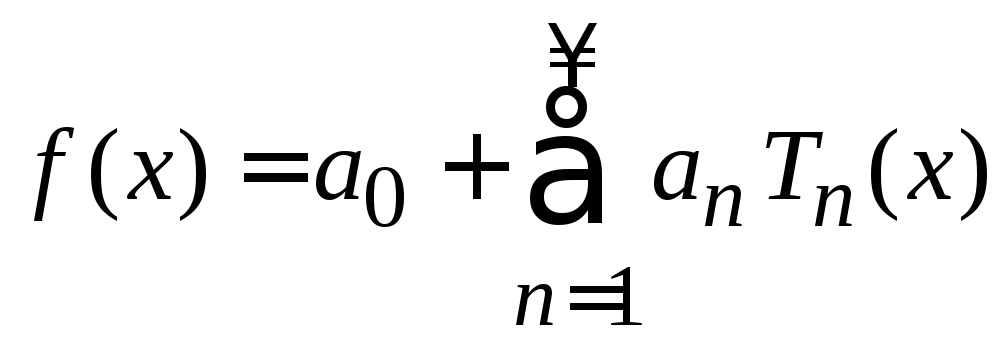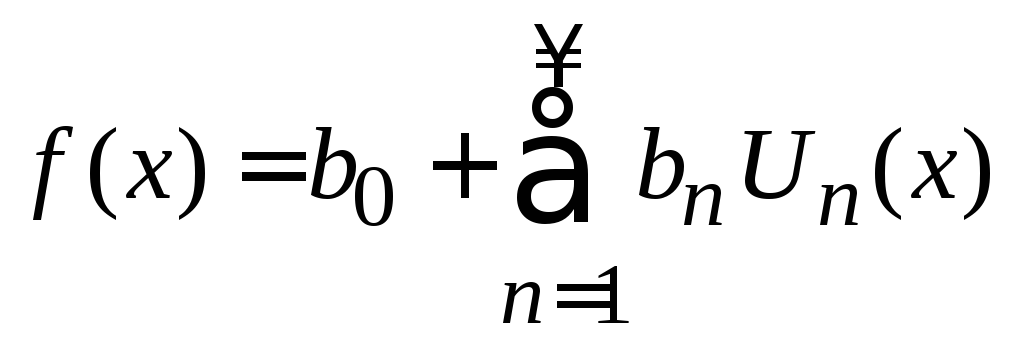. (6.168)

Используя

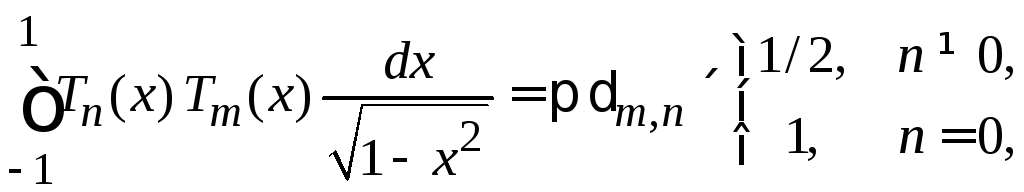(6.149)

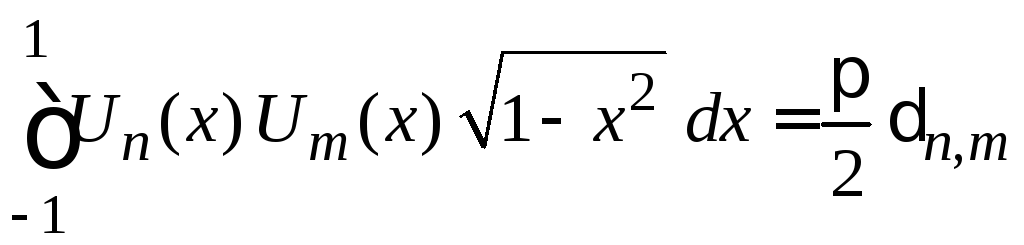, (6.167)

находим коэффициенты

,

,

,

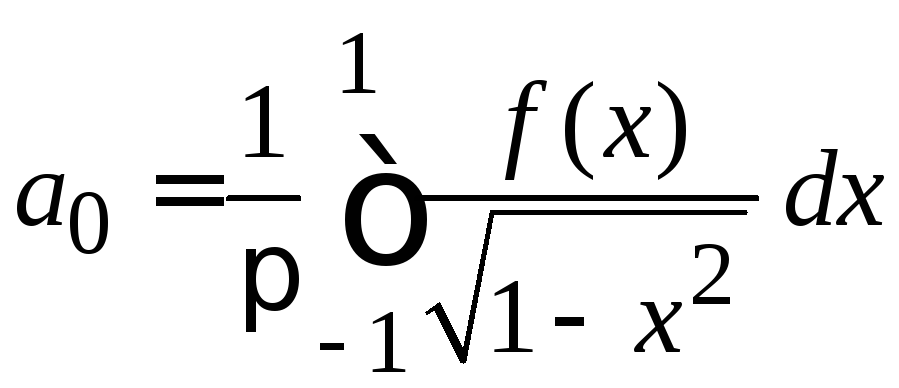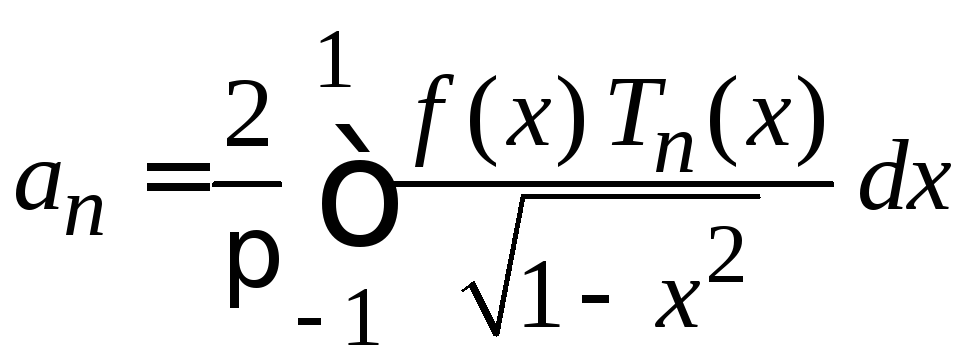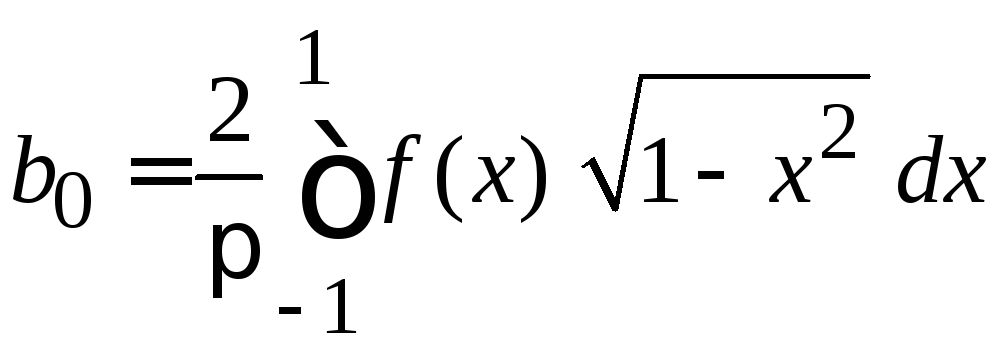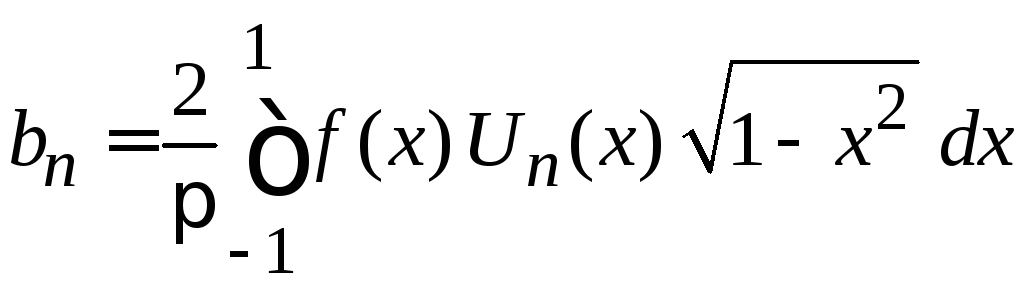. (6.169)

Аппроксимация полиномом

Исследуемая функция заменяется полиномом. В заданном интервале отклонение полинома от функции не превосходит определенного предела, вне интервала отклонение быстро увеличивается.

Полиномы Чебышева первого рода на интервале ограничены значениями

,

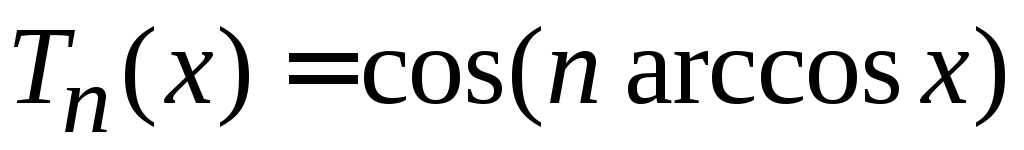, при .

Согласно

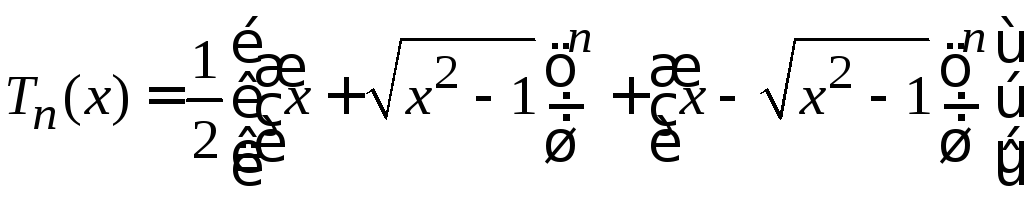, (6.153)

при полиномы возрастают с увеличениемn как геометрическая прогрессия

,

.

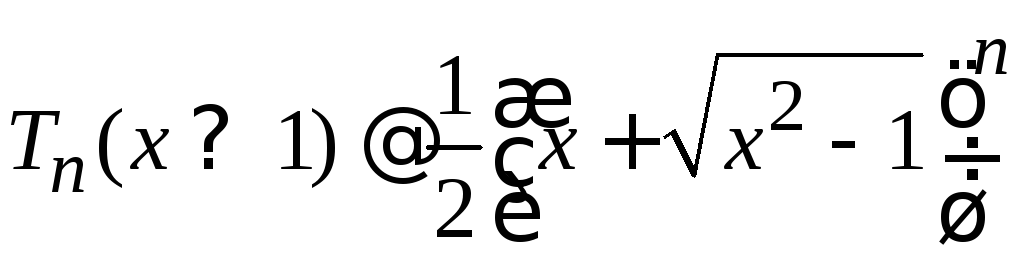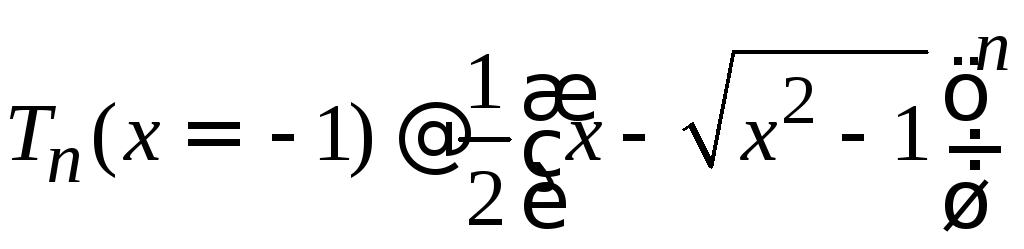Среди всех полиномов степени n, нормированных на одинаковый старший коэффициент, полиномы Чебышева ведут себя экстремально – они наименее отклоняются от нуля на интервале и максимально – вне этого интервала.

Фильтр нижних частот F(,₀)

Фильтр задерживает частоты  выше порогового значения ₀. Идеальный фильтр

.

Приближается к идеальному фильтру

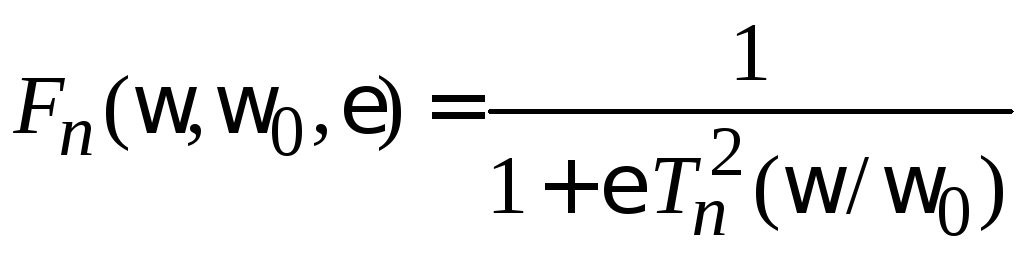. (6.172)

При ,– идеальный фильтр.

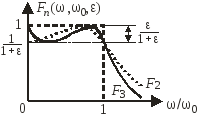
Фильтр нижних частот: ,и