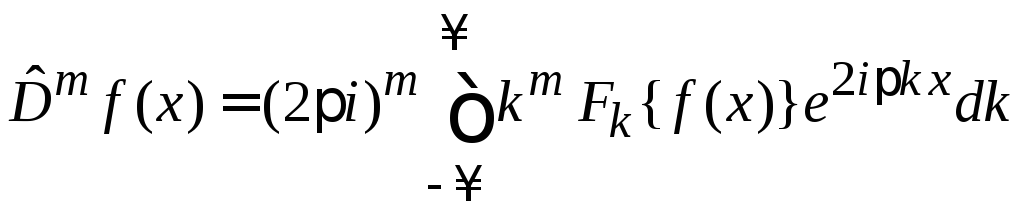Классические ортогональные полиномы

Полином (многочлен) порядка

.

Условие ортогональности

–орт,

–базис в гильбертовом пространстве с условием ортонормированности

,

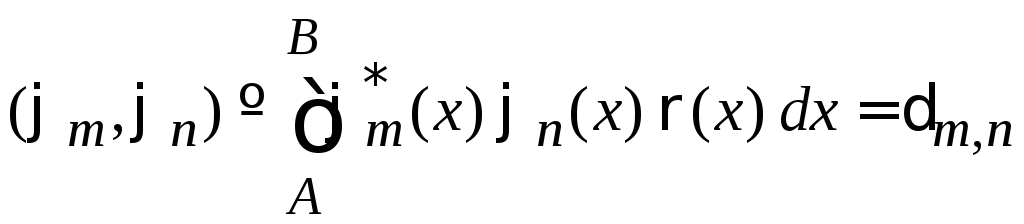где

–скалярное произведение функций;

–весовая функция;

–символ Кронекера.

Классические ортогональные полиномы некоторого типа являются частными решениями дифференциального уравнения обобщенного гипергеометрического типа – полиномы Эрмита, Лагерра, Лежандра, Чебышева, Якоби, Гегенбауэра.

Полиномы Эрмита

, ;.

Применяются в оптике, в математической статистике, в теории вероятностей, в квантовой механике.

Полиномы исследовали Пафнутий Львович Чебышев в 1859 г. и Шарль Эрмит в 1864 г., они называются также полиномами Чебышева–Эрмита.

Уравнение Эрмита

. (6.1)

Формула Родрига

Методом факторизации ранее получено решение (П.3.3). Доопределяем , тогда

. (6.2)

Весовая функция (П.3.1)

.

Из (6.2)

. (6.3)

Полиномы низших степеней

Из (6.2) с учетом

, ,, …

находим

, ,

, ,

, .

Полиномиальная форма

Обобщаем частные результаты

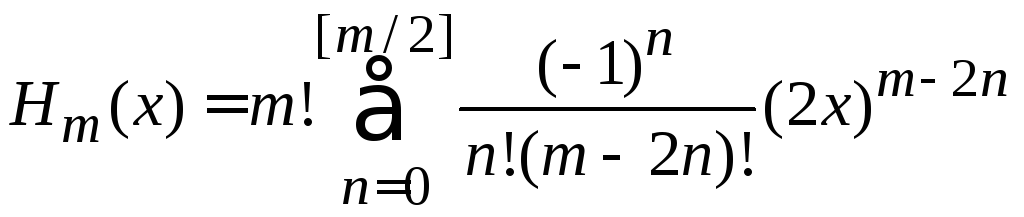, (6.4)

где – целая часть.

Интегральное представление

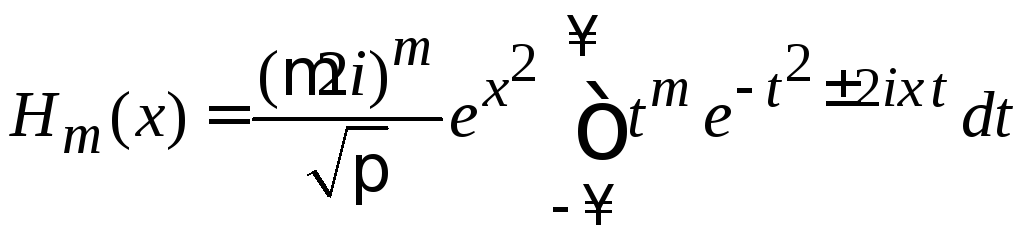(6.8)

применимо как для целых положительных m, так и для дробных и для отрицательных m.

Доказательство (6.8):

Теорема Фурье о дифференцировании

Для учитываем (П.2.6)

тогда

.

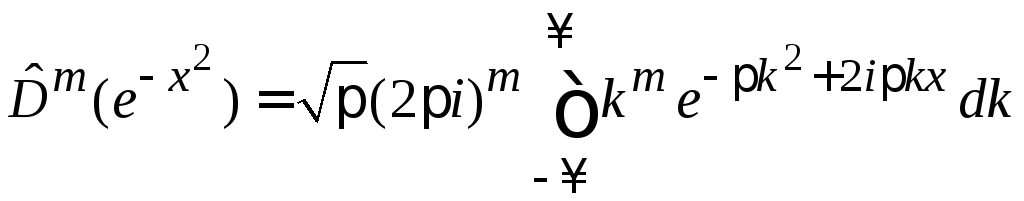Под интегралом заменяем :

,

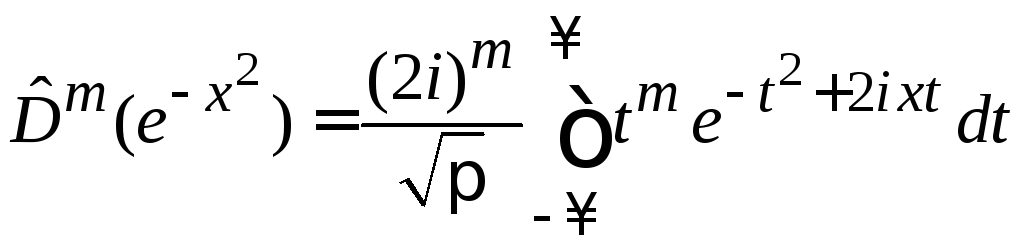Подстановка в (6.2)

дает

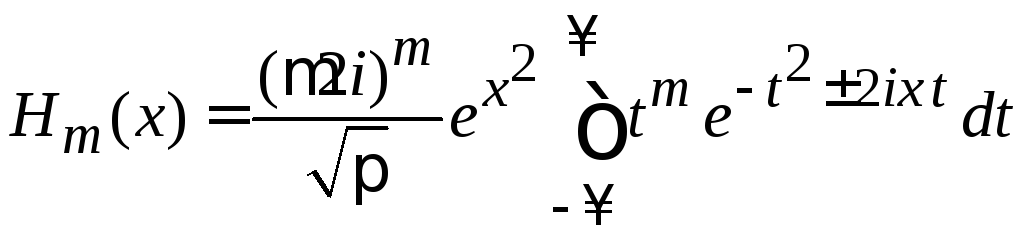, (6.8)

где комплексное сопряжение не меняет вещественный полином.

Производящая функция

Методом факторизации ранее получено (П.3.5)

. (6.10)

Из (5.14)

с получаем

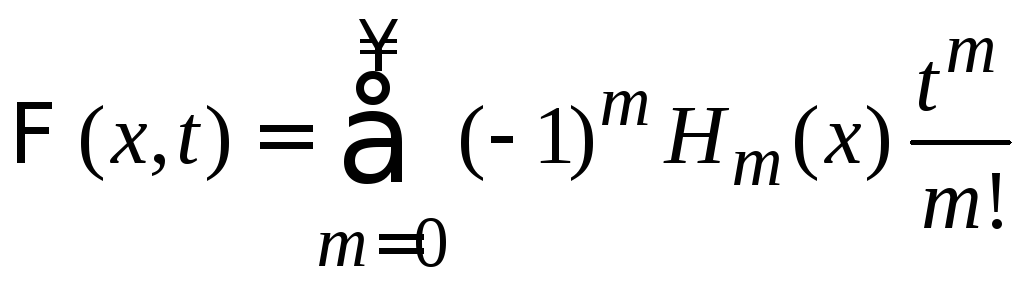. (6.11)

Рекуррентные соотношения для полиномов

Алгоритм получения:

1. Дифференцируем (6.10) по одному из аргументов.

2. В полученное соотношение подставляем (6.11).

3. Приравниваем слагаемые с одинаковыми степенями t.

Соотношение 1 для полинома Эрмита

Из

(6.10)

получаем

.

Подставляем (6.11)

,

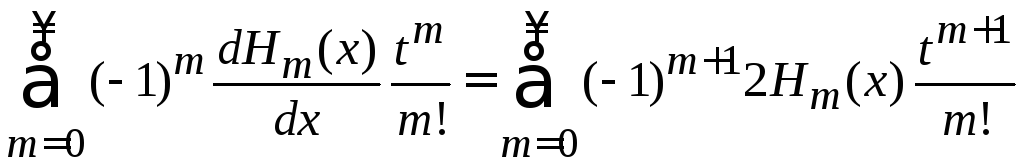приравниваем слагаемые с

,

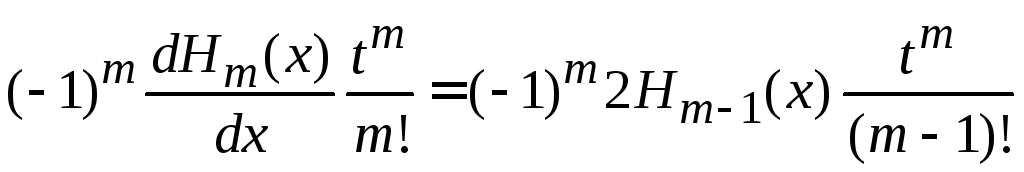получаем

, (6.12)

. (6.13)

Соотношение 2

Из

(6.10)

получаем

.

Подставляем

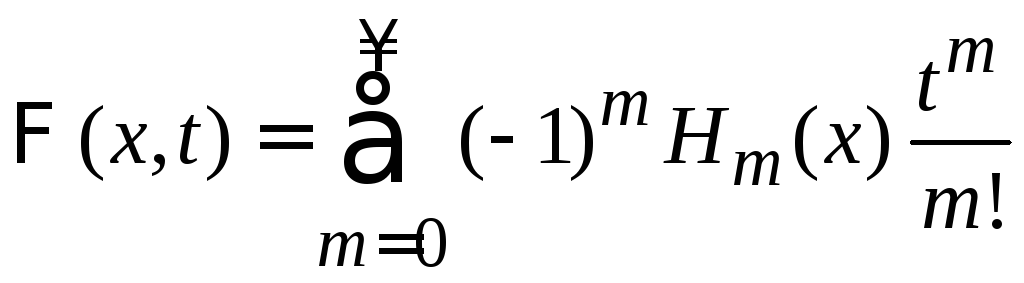, (6.11)

находим

,

приравниваем слагаемые с

,

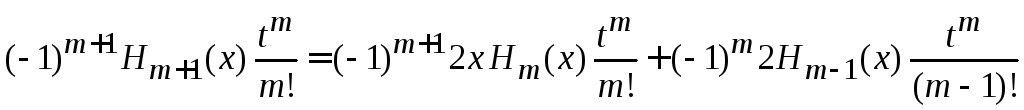получаем

. (6.15)

Учет

(6.12)

дает

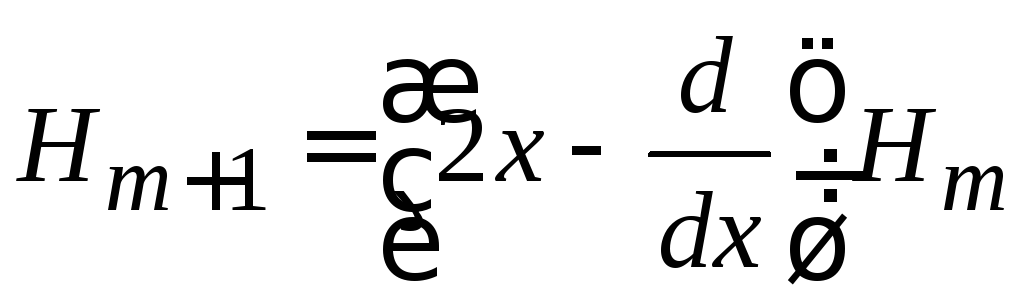. (6.16)

Условие ортонормированности

Множество образует базис в гильбертовом пространстве функций, определенных при ,с условием ортонормированности (П.3.4)

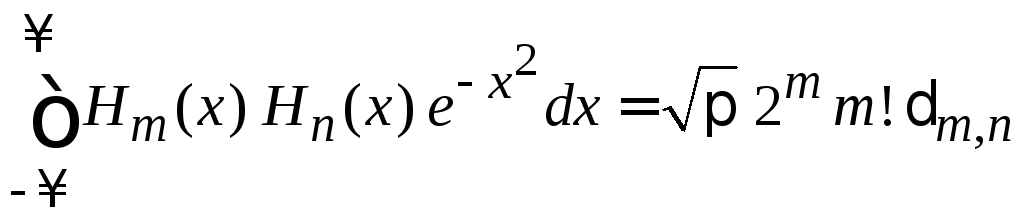. (6.18)

Разложение функции по полиномам Эрмита

Если определена при, то она разлагается по базису

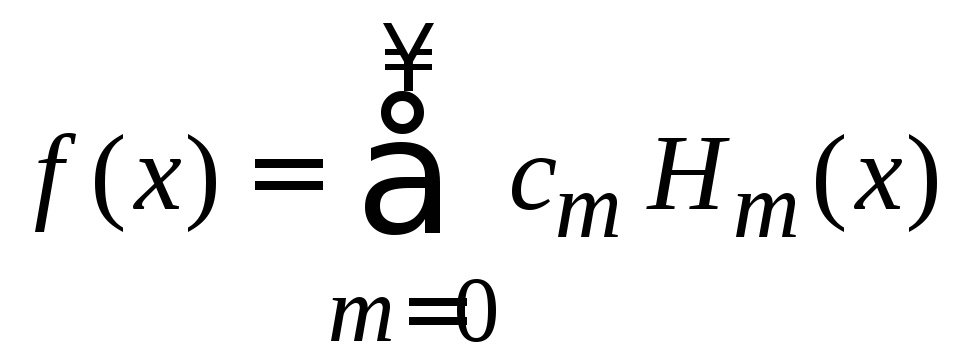. (6.19)

Находим коэффициент :

• умножаем (6.19) на ,

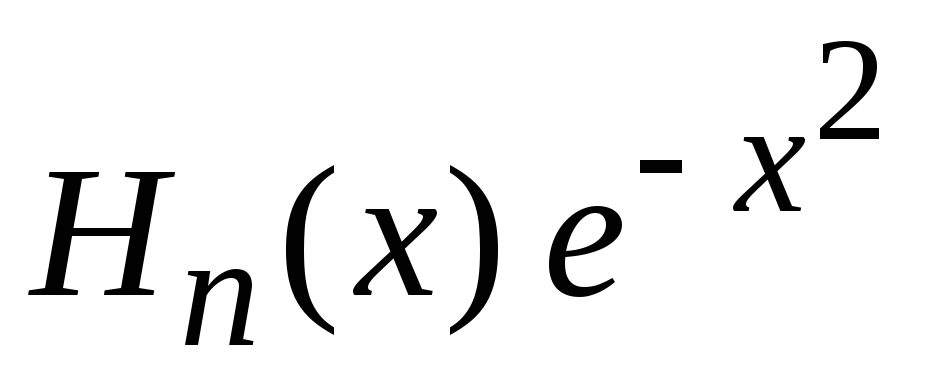• интегрируем по интервалу ,

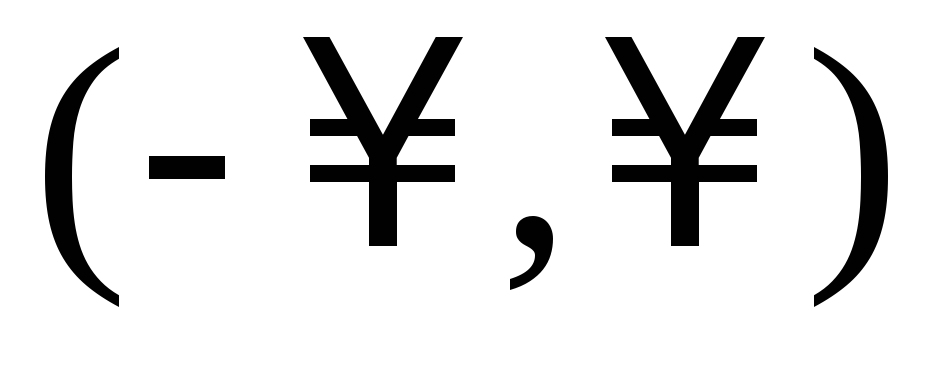• меняем порядок суммирования и интегрирования,

• учитываем ортонормированность (6.18),

• символ Кронекера снимает сумму, оставляя одно слагаемое:

.

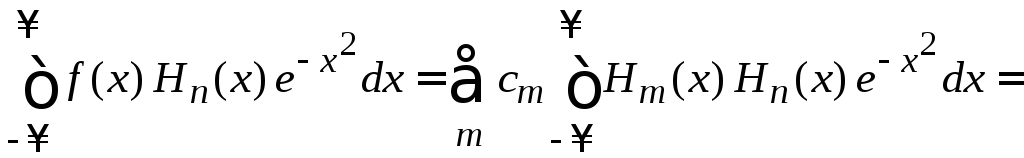
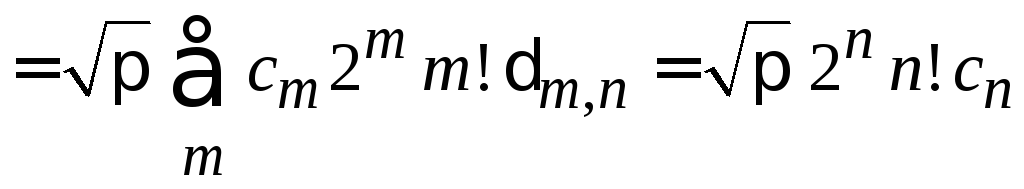Заменяем и получаем

.

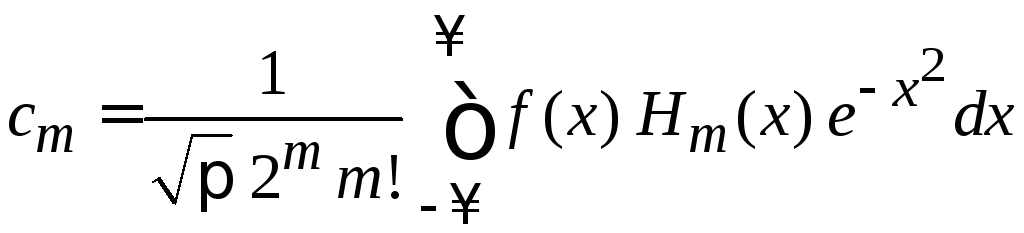• Подставляем полином в форме Родрига

, (6.2)

получаем

.

Интегрируем по частям m раз, свободные слагаемые зануляются на обоих пределах, получаем коэффициент

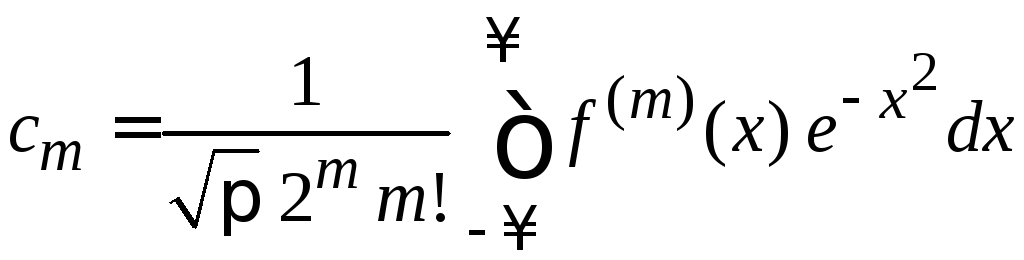. (6.20)