6. Анализ стационарного состояния отрезка линии с потерями

В теоретическом отношении стационарное состояние конечного и полубесконечного отрезков линии можно рассматривать как предельный случай (при ) гармонического процесса в них. Поэтому, полагая в формулах (9), (14) и (17), получим следующие выражения характеристических параметров линии в стационарном состоянии:

; ;,.

Формально, вид характеристик участков полубесконечных и конечных отрезков линии сохраняется и в стационарном состоянии. При из выражений (11) - (12) характеристик конечного участка[0,x] полубесконечного отрезка[0,] получаем

,

.

Для участка конечного отрезка линии, нагруженного пассивной ветвью с характеристиками и, аналогично находим:

• характеристики в экспоненциальных функциях

,

,

где значение коэффициента отражения по напряжению , определяемое отношением

,

ограничено замкнутым промежутком [–1,1](, алибо);

• характеристики в гиперболических функциях

,

.

Выражения (44) - (49) входных параметров участка конечного отрезка линии при переходят в вещественные функцииR(x) иG(x).

7. Анализ гармонического процесса в отрезке линии без потерь

   1. Комплексные характеристики отрезков линии без потерь

Формально, линия без потерь есть предельный случай линии с потерями при ограничении дуальной пары её первичных диссипативных параметров значениями R₀ = 0иG₀ = 0. В этом случае выражения характеристических параметров линии принимают наипростейший вид:

, следовательно,, (0)

, (0)

,, (0)

то есть собственное затухание линии без потерь равно нулю, а её характеристические сопротивление и проводимость вещественны. Поскольку коэффициент фазыпропорционален частоте, то фазовая скоростьv_ф= v_ф() волн напряжения и тока от частоты не зависит:

(0)

Для линий без потерь, моделирующих воздушные линии передачи, значение фазовой скорости v_фпо умолчанию принимают равным значению скорости света:v_ф= с = 3·10⁸м/с. Если же линия без потерь моделирует радиотехнический кабель, то это число делят на так называемый “коэффициент укорочения длины волны”, значения которого приводятся в стандарте на соответствующий кабель (ГОСТ 11326.1-79 – 11326.92-79).

При ,ииз выражений (18) - (19) комплексных характеристик участка [0, x] полубесконечного отрезка линии[0, )получаем

,;

и ,

причём и—синфазные гармонические колебания, поскольку векторыиколлинеарные.

Аналогично из (40 - 43) найдём выражения характеристик участка [0, x] конечного отрезка(0 x l)линии без потерь, нагруженного пассивной ветвью с характеристикамиили:

• характеристики в экспоненциальных функциях мнимого аргумента:

, (0)

, (0)

где через иобозначены комплексы действующих значений прямобегущих волн напряжения и тока в конце отрезка линии: и ;

• характеристики в гиперболических функциях записываются теперь в тригонометрических функциях вещественного аргумента:

, (0)

, (0)

поскольку

,.

Получим теперь выражение потребляемой комплексной мощности P_Sп(x)в сечении с координатойx конечного отрезка однородной линии:

=

=

.

2. Гармонические волны напряжения и тока

Если раскрыть скобки в (58) и (59), то образованные таким образом слагаемые в правых частях, как известно, можно рассматривать как комплексы действующих значений падающих и отражённых гармонических волн напряжения и тока. Учитывая, что, постоянные интегрирования U_п2иI_п2– комплексные числа с одинаковым значением аргументов:

,, а

получаем

,

.

Если из первых слагаемых u(x,t) иi(x,t)выделить составляющие, пропорциональные коэффициенту отражения, и объединить их с последними слагаемыми, представляющими отражённые волны, то получим разложение напряжения и тока набегущиеистоячие волны. Проще всего эту процедуру выполнить в комплексной форме. Обратившись к первому уравнению системы (58) - (59) выполним следующую цепочку преобразований:

.

После аналогичных преобразований второго уравнения той же системы получим

.

Прейдём теперь к мгновенным значениям напряжения u(x,t) и токаi(x,t) в отрезке линии без потерь:

,

.

Рис. 21

Эта пара выражений представляет так называемыесмешанныеволнынапряжения и тока (Рис. 21), поскольку их первые слагаемые описываютбегущиегармонические волны, а вторые –стоячие. Напомним, что одномерная стоячая волна представляется произведением двух функций, одна из которых зависит только от координаты x, а другая – только от относительного времениt.

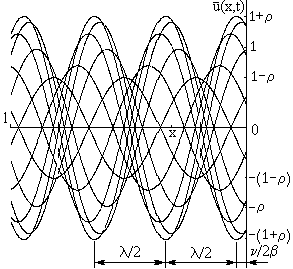
В зависимости от характера пассивной нагрузки в отрезке линии наблюдается один из трёх типов гармонического процесса:

• режим бегущих волн (при согласованнойнагрузке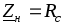или, когда);

• режим стоячих волн (для короткозамкнутого или разомкнутого на конце отрезка линии, а также при реактивной нагрузке либо, когда,);

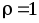• режим смешанных волн (при произвольной нагрузке или, когда,).