3. Комплексные погонные характеристики линии (комплексные телеграфные уравнения)

При возбуждении отрезка линии источником гармонического напряжения или тока с частотой установившиеся ток и напряжение его любого сечения изменяются также по гармоническому закону с тем же значением частоты. В этом случае, как и в теории цепей с сосредоточенными элементами, все расчёты значительно упрощаются, если применить комплексный анализ. Согласно правилам комплексного анализа вещественным гармоническим функциям напряжения и тока можно однозначно поставить в соответствие комплексные экспоненциальные функции – комплексы мгновенных значений этих величин:

, ,

над которыми и совершаются последующие линейные вещественные математические операции. Здесь U = U(x) и I = I(x) – комплексные функции вещественного аргумента x,называемые комплексами действующих значений напряжения и тока в сечении линии с координатойx.

Мгновенные значения этих величин вычисляются известным образом:

, , (0)

либо

, , (0)

в зависимости от вида вещественной гармонической функции времени, описывающей воздействие.

Рис. 2

Подставляя комплексы мгновенных значений напряжения и тока в систему телеграфных уравнений (2), получаем систему двух обыкновенных дифференциальных уравнений первого порядка

, (0)

, (0)

представляющих собой комплексныепогонныехарактеристики (комплексные телеграфные уравнения)однородной линии(Рис. 2). Введённые здесь обозначения и–это так называемые комплексные погонные параметры: продольное сопротивление и поперечная проводимость единицы длины однородной линии.

Преобразуем последнюю систему двух уравнений первого порядка к одному дифференциальному уравнению второго порядка относительно U=U(x)или I = I(x).Исключим, например, ток I = I(x).Дифференцируя первое уравнение и подставляя значениеdI(x)/dx из второго, найдём:

(0)

Точно такое же уравнение можно получить и для I = I(x):

(0)

Введём комплексный параметр , называемыйпостоянной (коэффициентом) распространенияи определяемый выражением

(0)

Для того, чтобы внести однозначность в определение , условимся в дальнейшем выбирать то значение корня, которое располагается в первом квадранте плоскости комплексной переменной. Вещественная часть постоянной распространения называетсякоэффициентом затухания, а мнимая– коэффициентом фазы(волновым числом). Более детально смысл этих величин обсуждается ниже.

С введением постоянной распространения комплексные телеграфные уравнения однородной линии примут вид:

и (0)

Уравнения такого вида в теории колебаний называют волновыми или уравнениями Гельмгольца.

4. Комплексные характеристики полубесконечного отрезка однородной линии

   1. Общее решение комплексных телеграфных уравнений

Рис. 3

Допустим, что реальная линия передачи настолько длинна, что её можно моделировать полуограниченной однородной линией (0x < . Как известно, общее решение уравнения Гельмгольца в общем случае можно записать в виде линейной комбинации либо экспонентexp(+x), exp(–x), либо гиперболических функций shx, chx.Однако для полубесконечного отрезка линии (Рис. 3) его общее решение, ограниченное на промежутке[0, ),должно содержать, очевидно, только одну убывающую экспоненту:

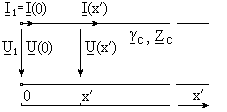
, (0)

. (0)

Постоянные интегрирования U(0) и I(0) характеристик конечного участка[0,x] полубесконечного отрезка линии[0, ) (11), (12) представляют собой комплексы действующих значений напряжения и тока в его начале. С другой стороны их можно рассматривать как комплексы действующих значений напряженияU₁= U(0) и тока I₁ = I(0)неавтономного двухполюсника, между которыми должна существовать линейная зависимость. Для установления этой связи обратимся к комплексным дифференциальным характеристикам однородной линии (5), (6). Комплекс действующего значения напряженияU(x)с учётом (12) будет определяться выражением

(0)

Обозначим

(0)

Это выражение называется характеристическим(волновым)сопротивлениемоднородной линии. Для определённости,из двух значений последнего корня для Z_c надо взять то, аргумент которого подчиняется неравенству

Сопоставляя выражения (11) и (13), находим Z-форму искомой линейной зависимости:

или . (0)

Справедливо и дуальное (в Y-форме) соотношение между рассматриваемыми величинами

или. (0)

Выражение

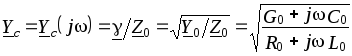(0)

при определяетхарактеристическую (волновую) проводимостьоднородной линии. Очевидно, характеристическое сопротивлениеZ_cи характеристическая проводимостьY_cявляются взаимообратными величинами

и.

Из формул (15), (16) следует, что, значения характеристических параметров Z_c иY_cоднородной линии совпадают со значениями сопротивления и проводимости её полубесконечного отрезка и, вполне естественно, его полубесконечного участка[x,), если определить их отношениями

и .

Однако, в отличие от значений сопротивления и проводимости сосредоточенного пассивного двухполюсника, находящихся в правой комплексной полуплоскости, включая её границу, значения характеристического сопротивления и характеристической проводимости однородной линии, располагаясь в той же полуплоскости, занимают более узкую область, заключённую между биссектрисами первого и четвёртого квадрантов или на её границе.

Постоянная распространения и характеристическое сопротивление(характеристическая проводимость) однородной линии представляют еёхарактеристические параметры.

Таким образом, число постоянных интегрирования в комплексных характеристиках конечного участка [0, x] полубесконечного отрезка линии[0, ) (11), (12) сокращается до единицы,и их можно записать в одной из двух форм:

, , (0)

либо

,(0)

Значение потребляемой комплексной мощности P_Sп(x), в сеченииxполубесконечного отрезка линии вычисляется как обычно:

,

где P_Sп(0) – значение потребляемой комплексной мощности в начале отрезка.