Практика 19. Определение предела функции по Коши

19.1.Предел функции в точке

Определение 1. Число A называется пределом функции f в точке a п о К о ш и, если

1.a предельная точка области определения функции f;

2.для каждого " > 0 существует такое число = (") > 0, что при всех x 6= a, удовлетворяющих условию jx aj < , справедливо неравенство jf(x) Aj < ", короче,

8 " > 0 9 (") > 0 : 8 x 0 < jx aj < ) jf(x) Aj < ":

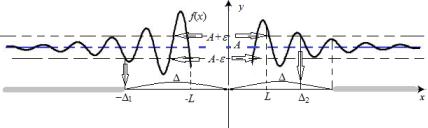
Рис. 1: Иллюстрация определения по Коши предела функции f в точке x = a .

Íà рисунке 1 графически задана некоторая функция f(x), не определенная в точке a, но имеющая предел в этой точке, поскольку

Теорема 19.1. Определения предела функции в точке по Коши и по Гейне эквивалентны.

Это означает, что можно пользоваться любым, каким удобнее для той или иной задачи.

p

8 " > 0 9 (") = 4 + " 2 > 0 : 8 x 0 < jx 2j < ) jx2 4j < ":

Согласно определению Коши это означает, что lim x2 = 4:

x!2

Можно и нужно сократить выкладки, воспользовавшись ограниченностью множителя (x + 2) в некоторой достаточно малой окрестности точки x = 2. Очевидно, что для всех x

таких, что jx 2j < 1 (т. е. 1 < x < 3) выполняется 3 < x + 2 < 5.

1

Рис. 2: Геометрическая оценка множителя (x + 2) в окрестности x = 2 .

Тогда для любого " > 0

вать выполнение неравенств (1) только при jx 2j < 1, так как при этом справедлива

19.2.Односторонние пределы

Наряду с окрестностями точки, когда точка лежит в некотором интервале, рассматривают промежутки, которые называют о д н о с т о р о н н и м и о к р е с т н о с т я м и то- чек. Полуинтервалы вида (a ; a] называют л е в о й - о к р е с т н о с т ь ю точки, а

полуинтервалы вида [a; a + ) п р а в о й - о к р е с т н о с т ь ю точки a.

Если точка a не входит в промежуток, левая (правая) -окрестность точки a называется п р о к о л о т о й.

Определение 2. Число A называют пределом функции f в т о ч к е a с п р а в а, если

1.a предельная точка области определения функции f;

2.для каждого " > 0 существует такое число = (") > 0, что при всех x, удовлетворяющих условию a < x < a + , справедливо неравенство jf(x) Aj < ", короче,

8 " > 0 9 (") > 0 : 8 x a < x < a + ) jf(x) Aj < ":

В этом случае пишут

1.a предельная точка области определения функции f;

2.для каждого " > 0 существует такое число = (") > 0, что при всех x, удовлетворяющих условию a < x < a, справедливо неравенство jf(x) Aj < ", короче,

8 " > 0 9 (") > 0 : 8 x a < x < a ) jf(x) Aj < ":

В этом случае пишут

Теорема 19.1. Функция имеет в точке предел тогда и только тогда, когда в этой точке существуют односторонние пределы, равные друг другу.

Во многих случаях можно определить с помощью соответствующих неравенств как подходит функция к своему пределу A: сверху (A+), снизу (A ) или с обеих сторон (A).

Пример 2. ( 407 б) Пусть y = f(x). Сформулировать с помощью неравенств, что значит

y ! b 0 ïðè x ! a 0:

Данная ситуация соответствует поведению функции, изображенном на рисунке 1 в левой проколотой окрестности точки x = a. Достаточно взять на оси Oy произвольную нижнюю "-окрестность точки y = b, так как y ! b 0, и по ней найти левую -окрестность точки x = a. 8 " > 0 9 (") > 0 : 8 x a < x < a ) b " < f(x) < b:

x!+0

19.3.Предел функции на бесконечности

Определение 4. Число A называют пределом функции f при x ! 1 п о К о ш и и

пишут A = lim f(x), если

x!1

1.существует число L > 0 такое, что функция f определена при всех jxj > L;

2.для каждого " > 0 существует такое число (") > 0, что при всех jxj > выполняется неравенство jf(x) Aj < ".

Рис. 3: Иллюстрация определения по Коши предела функции f на бесконечности.

Íà рисунке 3 графически задана некоторая функция f(x), имеющая предел равный числу A при x ! 1, поскольку

Пределы при x ! +1 (x ! 1) можно рассматривать, как односторонние пределы при x ! 1.

Пример 4. ( 404 б,в) Сформулировать с помощью неравенств следующие утверждения и привести соответствующие примеры:

Ïî рисунку 3 записать определения односторонних пределов при x ! 1 (x ! +1).

19.4.Бесконечный предел

Дадим определения случаям, когда пределом является не число, а бесконечность.

Определение 5. (п о К о ш и) Говорят, что предел функции f в точке a равен бесконеч-

ности, и пишут

lim f(x) = 1;

x!a

åñëè

1.a предельная точка области определения функции f;

2.для каждого E > 0 существует такое число (") > 0, что при всех x, удовлетворяющих условию 0 < jx aj < , выполняется неравенство jf(x)j > E.

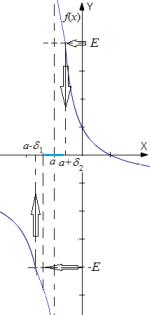
Рис. 4: Иллюстрация определения по Коши бесконечного предела функции f в точке a.

Íà рисунке 4 графически задана некоторая функция f(x), не определенная в точке a, но имеющая в этой точке бесконечный предел, поскольку

1. a предельная точка области определения функции f;