
- •1)Числовые множества. Структура множества действительных чисел. Свойства множества действительных чисел.
- •2)Числовые подмножества. Числовые промежутки. Окрестность точки
- •3) Ограниченные числовые множества, точные грани множеств.
- •4)Определение функции, основные свойства функции.
- •5)Обратные функции, основные свойства функции.
- •6)Определение числовой последовательности и ее предела.
- •7)Теорема о единственности предела числовой последовательности.
- •8)Теорема об ограниченности сходящейся числовой последовательности.
- •9)Арифметические действия над числовыми последовательностями
- •10)Теоремы о предельном переходе в неравенствах
- •11)Бесконечно большие и бесконечно малые последовательности. Связь между ними. Свойства бесконечно малых последовательностей.
- •12)Монотонные последовательности. Теоремы о пределах монотонных последовательностей.
- •13)Доказать , что последовательностьимеет предел.
- •14)Доказать, что
- •15)Подпоследовательности и частичные пределы. Теоремаы о подпоследовательностях.
- •16) Определение придела функции по Коши и по Гейне. Теорема об эквивалентности двух определений придела.
- •17)Односторонние пределы. Необходимое и достаточное условие существования предела функции.
- •18) Первый замечательный предел следствия из него.
- •19)Второй замечательный предел и следствия из него.
- •20)Сравнение бесконечно малых величин.
- •21)Определение порядка б.М. И выделение главной части б.М.
- •22)Вывести таблицу эквивалентных б.М.
- •23)Сравнение б.Б величин .
- •25)Непрерывность функции в точке. Необходимое и достаточное условие непрерывности в точке.
- •26) Классификация точек разрыва.
- •27)Непрерывность функции на множестве. Непрерывность элементарных функций.
- •28)Непрерывность сложной и обратной функции.
- •29) Первая и вторая теоремы Коши.
- •30) Первая и вторая теоремы Вейерштрасса.
- •31)Определение производной. Геометрический и физический смысл.
- •32)Односторонние производные. Необходимое и достаточное условие существования производной.
- •33)Правила вычисления производных от суммы , произведения и частного.
- •35)Производная обратной функции.
- •36) Производная функции заданной параметрически.
- •37)Производная неявно заданной функции.
- •39) Связь между непрерывностью и дифференцируемостью ф-и.
- •40) Определение дифференциала ф-и. Геометрический смысл дифференциала. Правила вычисления дифференциала.
- •43)Повторное дифференцирование в дифференциалах. Нарушение инвариантности формы высших дифференциалов.
- •44) Формула Тейлора для многочлена.
- •45)Формула Тейлора для произвольной ф-и.
- •46)Стандартные разложения. Определение числа e с точностью до 0,001.
- •47) Достаточное усл-е монотонности ф-и.
- •49) Достаточные условия экстремумафункции в точке
- •50) Достаточные условия выпуклости (вогнутости) ф-и. Определение выпуклой и вогнутой ф-и.
- •51) Точки перегиба. Достаточное условие точки перегиба.
- •52) Определение неопределенного интеграла. Свойства неопределенного интеграла.
- •53)Вывести таблицу интегралов из определения неопределенного интеграла .
- •54) Замена переменной в неопределенном интеграле.
- •55)Интегрирование по частям в неопределенном интеграле.
- •56. Понятие о рациональных и дробно-рациональных функциях. Разложение правильной рациональной дроби на сумму простейших дробей.
- •57) Интегрирование простейших дробей.
- •58. Вывод рекуррентной формулы.
- •60. Интегрирование дифференциального бинома. Подстановки Чебышева.
- •61. Подстановки Эйлера.
- •62. Интегрирование тригонометрических функций.
- •63. Определение интеграла Римана. Функции, интегрируемые по Риману.
- •64. Свойства интеграла Римана, выражаемые равенствами.
- •65. Свойства интеграла Римана, выражаемые равенствами.
- •66. Основная теорема интегрального исчисления.
- •67. Замена переменной в определенном интеграле.
- •68) Интегрирование по частям в определенном интеграле.
- •69) Вычисление площадей плоских фигур в декартовых координатах.
- •70) Площадь плоской фигуры в параметрическом виде.
- •71) Площадь плоской фигуры в полярных координатах.
- •72. Вычисление длины дуги в декартовых координатах.
- •73. Вычисление длины дуги в параметрическом виде.
- •74. Вычисление длины дуги в полярных координатах.
- •75) Понятия о двух типах несобственных интегралов
56. Понятие о рациональных и дробно-рациональных функциях. Разложение правильной рациональной дроби на сумму простейших дробей.
Опред.1:
ф-я, равная отношению двух многочленов,
назыв. дробно-рациональной ф-ей, или
рациональной дробью.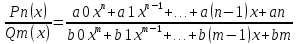 ,
(m,nϵN,
a0,
a1,
…, an,
b0,
b1,
…, bm
– действительные числа, a0≠0,
b0≠0).
,
(m,nϵN,
a0,
a1,
…, an,
b0,
b1,
…, bm
– действительные числа, a0≠0,
b0≠0).
Опред.2: рациональная дробь называется правильной, если степень многочлена, стоящего в числителе, меньше степени многочлена, стоящего в знаменателе(n<m). В противном случае рациональная дробь называется неправильной.
Всякую неправильную рациональную дробь путем деления числителя на знаменатель можно представить в виде многочлена и правильной рациональной дроби.
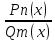 =
Ln-m(x)
+
=
Ln-m(x)
+
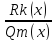 ,
гдеLn-m(x)-многочлен
степени n-m),
Rk(x)
– многочлен степени k,
где k<m,
т.е.
,
гдеLn-m(x)-многочлен
степени n-m),
Rk(x)
– многочлен степени k,
где k<m,
т.е.
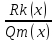 – правильная рациональная дробь.
– правильная рациональная дробь.
Интегрирование
правильной рациональной дроби сводится
к разложению ее на сумму простейших
дробей. Для этого необходимо найти
корни знаменателя, т.е. решить ур-е
Qm(x)=0
и разложит знаменатель на сомножители.
Если в этом разложении x=a
является действительным корнем первой
кратности(т.е. встречается один раз),
то ему соответствует простейшая дробь
вида
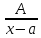 ,
где А-неизвестный коэффициент, подлежащий
определению.
,
где А-неизвестный коэффициент, подлежащий
определению.
Если
x=a
явл. действительным корнем кратности
k(т.е.
в разложении встречается k
раз), то ему соответствует сумма k
дробей вида
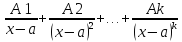 ,
гдеA1,
A2,
…, Ak
– неизвестные коэффициенты, подлежащие
определению.
,
гдеA1,
A2,
…, Ak
– неизвестные коэффициенты, подлежащие
определению.
Если
знаменатель Qm
имеет комплексно-сопряженные корни
первой кратности, то они определяются
квадратным трехчленом x2+px+q,
D=p2-4q<0.
Этой паре комплексно-сопряженных корней
соответствует
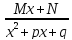 ,
гдеM,N
– неизвестные коэффициенты, подлежащие
определению.
,
гдеM,N
– неизвестные коэффициенты, подлежащие
определению.
Если
комплексно-сопряженные корни имеют
кратность k,
то им соответствует сумма k
дробей вида
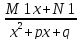 +
+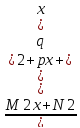 +
… +
+
… +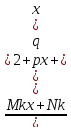 ,
гдеMi,
Ni(i=1,2,…,k)
– неизвестные корни, подлежащие
определению.
,
гдеMi,
Ni(i=1,2,…,k)
– неизвестные корни, подлежащие
определению.
________________________________________________________________________
57) Интегрирование простейших дробей.
Опред.:
простыми или простейшими рациональными
дробями назыв. дроби вида:
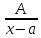 ,
,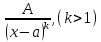 ,
,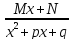 ,
,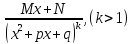 ,
гдеA,
a,
M,
N,
p,
q
– действительные числа, k-натуральное
число, а квадратный трехчлен x2+Px+q
не имеет действительных корней, т.е.
D=p2-4q<0.
,
гдеA,
a,
M,
N,
p,
q
– действительные числа, k-натуральное
число, а квадратный трехчлен x2+Px+q
не имеет действительных корней, т.е.
D=p2-4q<0.
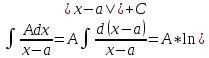
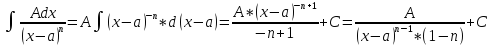
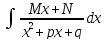 ,
D=p2-4q<0
,
D=p2-4q<0
При
интегрировании используется метод
интегрирования квадратного трехчлена,
выделяется полный квадрат
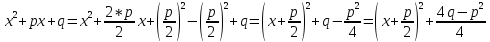
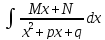 =
(выделяем полный квадрат в знаменателе)
=
=
(выделяем полный квадрат в знаменателе)
=
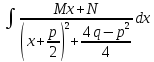 = (заменаx+(p/2)=t,
x=t-(p/2),
dx=dt,
0<
= (заменаx+(p/2)=t,
x=t-(p/2),
dx=dt,
0<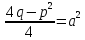 )
=
)
=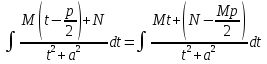 (разбиваем на два интеграла, один
содержитt,
другой нет) =
(разбиваем на два интеграла, один
содержитt,
другой нет) =
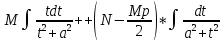 = =
= =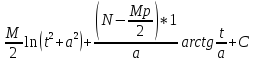 =
=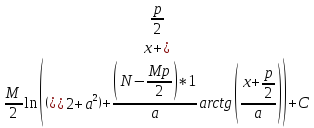 =
=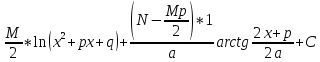 ,
где
,
где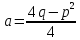
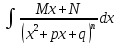 =
=
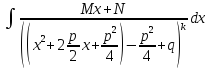 =
=
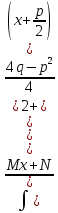 = (заменаx+(p/2)=t,
x=t-(p/2),
dx=dt,
0<
= (заменаx+(p/2)=t,
x=t-(p/2),
dx=dt,
0<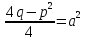 )
=
)
=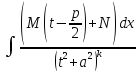 =
=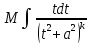 +
+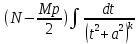 = =
= =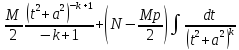 =
=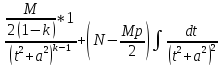 .
.
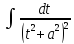 вычисляется
по рекуррентной формуле.
вычисляется
по рекуррентной формуле.
________________________________________________________________________
58. Вывод рекуррентной формулы.
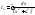 =
=
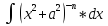 =
|
=
|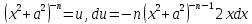 = =
= =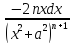 , dv=dx, v=x | =
, dv=dx, v=x | =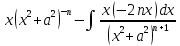 =
=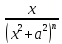 +
+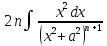 = =
= =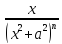 +
+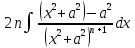 =
=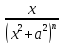 +
+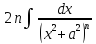 -
-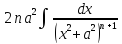 =
=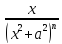 + 2nIn
– 2na2In+1
+ 2nIn
– 2na2In+1
In
=
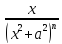 + 2nIn
– 2na2In+1
=> 2na2In+1
=
+ 2nIn
– 2na2In+1
=> 2na2In+1
=
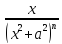 + (2n-1)In
|/2na2
+ (2n-1)In
|/2na2
In+1
=
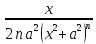 +
+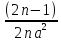 In
= |n+1=k, n=k-1|
In
= |n+1=k, n=k-1|
Ik
=
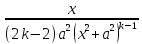 +
+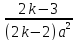 Ik-1
Ik-1
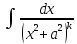 =
=
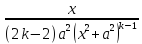 +
+
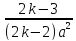 *
*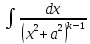 ,
(k>1)
,
(k>1)
________________________________________________________________________
59. Интегрирование иррациональных ф-й. Дробно-рациональные подстановки.
Интегрирование иррациональных выражений производится методом рационализации подынтегрального выражения. Суть метода состоит в том, что с помощью определенных замен под знаком получают рациональную дробь, которую можно интегрировать стандартными способами, разложив на простейшие дроби.
Вычисление интегралов вида
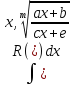 ,
где К – рациональная ф-я своих аргументов,a,
b,
c,
у – действительные числа, m≥2
– натуральное число. Обязательно в
этом интеграле под корнем стоит
дробно-линейная ф-я, которая в частном
случае может быть линейной.
,
где К – рациональная ф-я своих аргументов,a,
b,
c,
у – действительные числа, m≥2
– натуральное число. Обязательно в
этом интеграле под корнем стоит
дробно-линейная ф-я, которая в частном
случае может быть линейной.
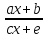 –дробно-линейная
ф-я(отношение двух линейных ф-й). если
c=0,
e=1
=> ax+b
–дробно-линейная
ф-я(отношение двух линейных ф-й). если
c=0,
e=1
=> ax+b
Интегралы
такого вида вычисляются с помощью
замены
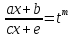 .
.
Покажем, что такая замена приводит к рационализации подынтегрального выражения. Выразим x и найдем dx.
ax+b=cxtm+etm
=> x(a-ctm)=etm-b
=> x=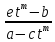 – рациональная дробь
– рациональная дробь
dx=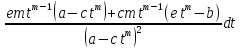 =
=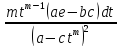
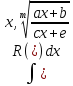 =
=
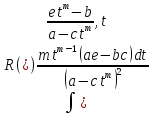 ч.т.д.
ч.т.д.
Вычисление интегралов вида
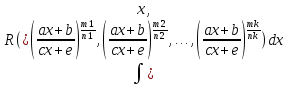 ,
гдеR-рациональная
ф-я своих аргументов, a,b,c,e
– действительные числа,
,
гдеR-рациональная
ф-я своих аргументов, a,b,c,e
– действительные числа,
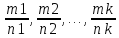 – несократимые дроби.
– несократимые дроби.
Замена
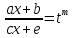 ,
где – общий знаменатель дробей
,
где – общий знаменатель дробей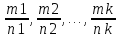 .
.
Покажем, что в этом случае снова получаем рациональную дробь.
Из
предыдущего известно, что x=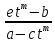 ,dx
=
,dx
=
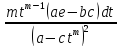 .
.
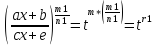 ,
где r1
– целое число
,
где r1
– целое число
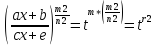 ,
где r2
– целое число
,
где r2
– целое число
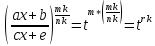 ,
где rk
– целое число
,
где rk
– целое число
В
результате получаем интеграл:
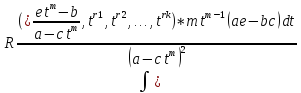 .
ч.т.д.
.
ч.т.д.
________________________________________________________________________
