
- •1)Числовые множества. Структура множества действительных чисел. Свойства множества действительных чисел.
- •2)Числовые подмножества. Числовые промежутки. Окрестность точки
- •3) Ограниченные числовые множества, точные грани множеств.
- •4)Определение функции, основные свойства функции.
- •5)Обратные функции, основные свойства функции.
- •6)Определение числовой последовательности и ее предела.
- •7)Теорема о единственности предела числовой последовательности.
- •8)Теорема об ограниченности сходящейся числовой последовательности.
- •9)Арифметические действия над числовыми последовательностями
- •10)Теоремы о предельном переходе в неравенствах
- •11)Бесконечно большие и бесконечно малые последовательности. Связь между ними. Свойства бесконечно малых последовательностей.
- •12)Монотонные последовательности. Теоремы о пределах монотонных последовательностей.
- •13)Доказать , что последовательностьимеет предел.
- •14)Доказать, что
- •15)Подпоследовательности и частичные пределы. Теоремаы о подпоследовательностях.
- •16) Определение придела функции по Коши и по Гейне. Теорема об эквивалентности двух определений придела.
- •17)Односторонние пределы. Необходимое и достаточное условие существования предела функции.
- •18) Первый замечательный предел следствия из него.
- •19)Второй замечательный предел и следствия из него.
- •20)Сравнение бесконечно малых величин.
- •21)Определение порядка б.М. И выделение главной части б.М.
- •22)Вывести таблицу эквивалентных б.М.
- •23)Сравнение б.Б величин .
- •25)Непрерывность функции в точке. Необходимое и достаточное условие непрерывности в точке.
- •26) Классификация точек разрыва.
- •27)Непрерывность функции на множестве. Непрерывность элементарных функций.
- •28)Непрерывность сложной и обратной функции.
- •29) Первая и вторая теоремы Коши.
- •30) Первая и вторая теоремы Вейерштрасса.
- •31)Определение производной. Геометрический и физический смысл.
- •32)Односторонние производные. Необходимое и достаточное условие существования производной.
- •33)Правила вычисления производных от суммы , произведения и частного.
- •35)Производная обратной функции.
- •36) Производная функции заданной параметрически.
- •37)Производная неявно заданной функции.
- •39) Связь между непрерывностью и дифференцируемостью ф-и.
- •40) Определение дифференциала ф-и. Геометрический смысл дифференциала. Правила вычисления дифференциала.
- •43)Повторное дифференцирование в дифференциалах. Нарушение инвариантности формы высших дифференциалов.
- •44) Формула Тейлора для многочлена.
- •45)Формула Тейлора для произвольной ф-и.
- •46)Стандартные разложения. Определение числа e с точностью до 0,001.
- •47) Достаточное усл-е монотонности ф-и.
- •49) Достаточные условия экстремумафункции в точке
- •50) Достаточные условия выпуклости (вогнутости) ф-и. Определение выпуклой и вогнутой ф-и.
- •51) Точки перегиба. Достаточное условие точки перегиба.
- •52) Определение неопределенного интеграла. Свойства неопределенного интеграла.
- •53)Вывести таблицу интегралов из определения неопределенного интеграла .
- •54) Замена переменной в неопределенном интеграле.
- •55)Интегрирование по частям в неопределенном интеграле.
- •56. Понятие о рациональных и дробно-рациональных функциях. Разложение правильной рациональной дроби на сумму простейших дробей.
- •57) Интегрирование простейших дробей.
- •58. Вывод рекуррентной формулы.
- •60. Интегрирование дифференциального бинома. Подстановки Чебышева.
- •61. Подстановки Эйлера.
- •62. Интегрирование тригонометрических функций.
- •63. Определение интеграла Римана. Функции, интегрируемые по Риману.
- •64. Свойства интеграла Римана, выражаемые равенствами.
- •65. Свойства интеграла Римана, выражаемые равенствами.
- •66. Основная теорема интегрального исчисления.
- •67. Замена переменной в определенном интеграле.
- •68) Интегрирование по частям в определенном интеграле.
- •69) Вычисление площадей плоских фигур в декартовых координатах.
- •70) Площадь плоской фигуры в параметрическом виде.
- •71) Площадь плоской фигуры в полярных координатах.
- •72. Вычисление длины дуги в декартовых координатах.
- •73. Вычисление длины дуги в параметрическом виде.
- •74. Вычисление длины дуги в полярных координатах.
- •75) Понятия о двух типах несобственных интегралов
53)Вывести таблицу интегралов из определения неопределенного интеграла .
Таблица интегралов.
1)
∫xαdx
=
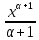 +C
(α≠-1)
+C
(α≠-1)
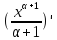 =
=
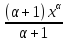 =xα
=xα
2)
α=-1
=> ∫x-1dx
= ∫ =ln|x|+C
=ln|x|+C
ln|x|=ln(x) при x>0 и ln(-x) при x<0
(ln|x|)’= 1/x при x>0 и 1/x при x<0
∫
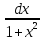 =
arctgx
+ C
или –arctgx
+ C
=
arctgx
+ C
или –arctgx
+ C∫
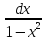 =
=
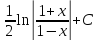
∫
 =
arcsinx + C или
–arcsinx + C
=
arcsinx + C или
–arcsinx + C∫
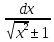 =
ln|x+
=
ln|x+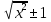 |+C
= (+)Arshx + Cили
(-) Archx + C
|+C
= (+)Arshx + Cили
(-) Archx + C∫axdx =
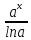 + C
+ C∫exdx = ex + C
∫sinxdx = -cosx + C
∫cosxdx = sinx + C
∫
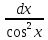 =
tgx + C
=
tgx + C∫
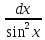 =
ctgx
+ С
=
ctgx
+ С∫shxdx = chx + C
∫chxdx = shx + C
∫
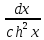 =
thx + C
=
thx + C∫
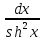 =
-cthx + C
=
-cthx + C
Дополнение к таблице интегралов.
1)
∫ =
=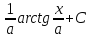
∫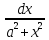 =
∫
=
∫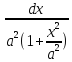 =
=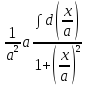 =
=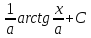
2)
∫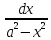 =
=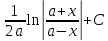
∫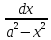 =
=
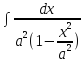 =
=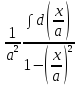 =
=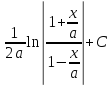 =
=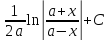
∫
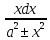 =
=
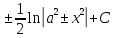
∫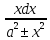 =
=
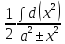 =
=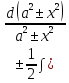 =
=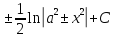
4)
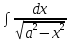 = arcsin
= arcsin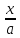 + C
+ C
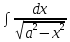 =
=
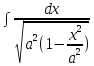 =
=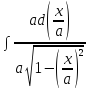 = arcsin
= arcsin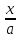 + C
+ C
5)
 = ln|x +
= ln|x +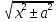 |
+ C
|
+ C
 =
=
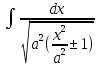 =
=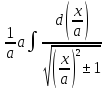 =
=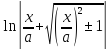 + C =
+ C =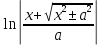 +C=
ln|x +
+C=
ln|x +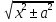 |
- lna + C = ln|x +
|
- lna + C = ln|x + |
+ C1
|
+ C1
6)
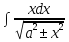 = ±
= ±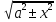 + C
+ C
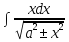 =
=
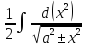 =
=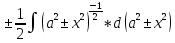 =
=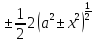 + C = =±
+ C = =±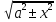 + C
+ C
7)
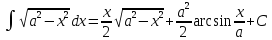
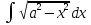 =
|x=asint, dx=acostdt,
=
|x=asint, dx=acostdt,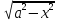 =acost|
=
=acost|
=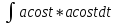 = =
= =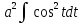 =
=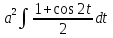 =
=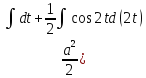 =
=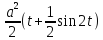 + C = =
+ C = =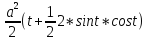 + C =
+ C =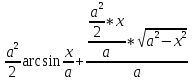 + C =
+ C =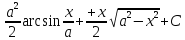 ,при
cos2t=
,при
cos2t=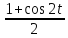 ,
sint=x/a, cost=
,
sint=x/a, cost=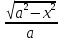 ,
t=arcsin(x/a).
,
t=arcsin(x/a).
8)
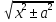 dx
=
dx
=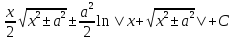
________________________________________________________________________
54) Замена переменной в неопределенном интеграле.
Теорема: пусть ф-я x=ϕ(t) определена и дифференцируема на (α;β), а мн-во ее значений есть (a,b).
Пусть для ф-и f(x) на (a,b) существует первообразная F(x), т.е. ∫f(x)dx= F(x)+C.Тогда всюду на (α;β) существует первообразная для ф-и f(ϕ(t))*ϕ’(t) и имеет место ф-ла
∫f(x)dx = ∫f(ϕ(t))*ϕ’(t)dt = F(ϕ(t)) + C
Док-во: F(x) – первообразная для f(x). найдем дифференциал d(F(ϕ(t))+C)=(F(ϕ(t))+C)t’dt = =F’(ϕ(t))*ϕ’(t)dt = f(ϕ(t))*ϕ’(t)dt => ∫f(ϕ(t))*ϕ’(t)dt = F(ϕ(t))+C (1)
d(F(ϕ(t))+C)=f(ϕ(t))*ϕ’(t)dt=f(x)dx при x=ϕ(t), ϕ’(t)dt=xt’dt=dx
∫f(x)dx=f(ϕ(t))+C (2)
Объединяя (1) и (2)б, получаем:
∫f(x)dx=∫f(ϕ(t))*ϕ’(t)dt=F(ϕ(t))+C. полученная ф-ла назыв. ф-лой замены переменной в неопределенном интеграле.
В некоторых примерах, когда под знаком корня стоят выр-я, содержащие x2б аналогичные замены ен приводят к верному решению. Для интегралов такого вида сещуствуют спец. Замены:
∫R(x,
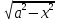 )dx
=>замена
x=asint, dx=arccost+dt(a>0)
)dx
=>замена
x=asint, dx=arccost+dt(a>0)
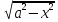 =
=
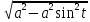 =
=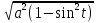 =
=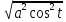 = a|cost| = acost
= a|cost| = acost
x=asint
=> sint =
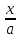 => t=arcsin
=> t=arcsin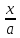 ,
tϵ[
,
tϵ[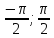 ], cost>0
], cost>0
∫R(x,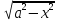 )dx
= ∫R(asint, acost)*acostdt
)dx
= ∫R(asint, acost)*acostdt
∫R(x,
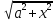 )dx
=>замена
x=asht, dx=acht+dt(a>0)
)dx
=>замена
x=asht, dx=acht+dt(a>0)
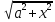 =
=
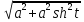 =
=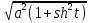 =
=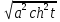 = a|cht| = acht
= a|cht| = acht
ch2t – sh2t = 1
∫R(x,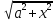 )dx
= ∫R(asht, acht)*achtdt
)dx
= ∫R(asht, acht)*achtdt
Либо:
x=atgt,
dx=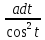
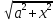 =
=
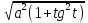 =
=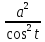 =
=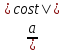 =
=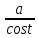
1
+ tg2t
= 1 +
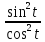 =
=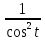
x=atgt
=> tgt =
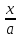 => t = arctg
=> t = arctg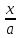 ,
tϵ[
,
tϵ[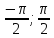 ]
]
∫R(x,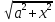 )dx
= ∫R(atgt,
)dx
= ∫R(atgt,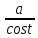 )
)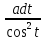
∫R(x,
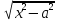 )dx
=>замена
x=acht, dx=ashtdtб
либо
x=
)dx
=>замена
x=acht, dx=ashtdtб
либо
x=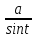
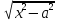 =
=
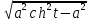 =
=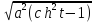 =
=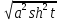 = a|sht| = asht
= a|sht| = asht
∫R(x,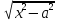 )dx
= ∫R(acht, asht)*ashtdt
)dx
= ∫R(acht, asht)*ashtdt
Либо:
x=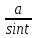 ,dx=
,dx=
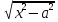 =
=
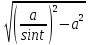 =
=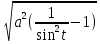 =
=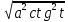 = a|ctgt|= actgt.
= a|ctgt|= actgt.
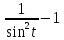 =
= =
=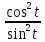 = ctg2t
= ctg2t
∫R(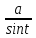 ,actgt)actgtdt.
,actgt)actgtdt.
________________________________________________________________________
55)Интегрирование по частям в неопределенном интеграле.
Теор.: пусть каждая из ф-й u(x) и v(x) определены и диффер. на (a,b) и пусть на этом мн-ве сущ. первообразная для ф-и u(x)*v’(x). Тогда на (a,b) сущ. первообразная для ф-и v(x)*u‘(x) и имеет место ф-ла ∫u(x)*v’(x)dx = uv - ∫v(x)*u’(x)dx или ∫udv = uv - ∫vdu.
Док-во: рассмотрим дифференциал d(uv) = vdu + udv
udv = d(uv) – vdu |∫ => ∫udv = ∫d(uv) - ∫vdu
∫udv = uv - ∫vdu – формула интегрирования по частям
Для применения этой формулы подынтегральные выр-я нужно представить в виде одной ф-и на дифференциал другой ф-и.
Применяется к ∫ след вида:
∫f(x)dx, где f(x) – обратная ф-я
f(x)
= {lnx,
 ,arcsinx,
arccosx,
arctgx,
arcctgx},
f(x)=u,
dx=dv
,arcsinx,
arccosx,
arctgx,
arcctgx},
f(x)=u,
dx=dv
∫f(x)P(x)dx, где f(x)= {lnx,
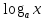 ,arcsinx,
arccosx,
arctgx,
arcctgx},
f(x)=u,
P(x)dx=dv,
P(x)
– рациональная или иррациональная
ф-я.
,arcsinx,
arccosx,
arctgx,
arcctgx},
f(x)=u,
P(x)dx=dv,
P(x)
– рациональная или иррациональная
ф-я.∫P(x)f(x)dx, где P(x)-многочлен, f(x) = {ex, ax, sinx, cosx, tgx, ctgx}, P(x)=г
∫eaxcosbxdx и ∫eaxsinbxdx – круговые интегралы.
Эти интегралы вычисляются 2 раза по частям. В результате двукратного применения ф-лы интегрирования по частям, в правой части получаем такой же интеграл, что и в левой. Вычисляем этот интеграл, решая алгебраическое уравнение. В круговых интегралах не важно, какую из ф-й обозначить за u.
eiϕ=cosϕ+isinϕ, cosϕ=Re eiϕ, sinϕ=Im eiϕ. Re-действительная часть, Im-мнимая часть.
________________________________________________________________________
