Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4612 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Белорусский государственный технологический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

метода, MCad6

.0.pdf
Скачиваний:
18
Добавлен:
26.03.2015
Размер:
1.17 Mб
Скачать
☆

Для нахождения корней полинома, т.е. для решения

уравнения a

n

x n + a

n−1

x n−1

+... + a x + a

0

= 0 используется

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

функция polyroots(v), где v - вектор коэффициентов

полинома. vT = (a

, a ,..., a

n−1

, a

n

). Функция возвращает вектор

 

 

 

 

 

 

 

 

 

0

 

1

 

 

 

 

 

 

элементами которого являются корни полинома.

Пример. Найти все корни уравнения x3 + 2x 2 − x − 2 = 0

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

v

 

 

 

 

 

1

- определяем вектор коэффициентов

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

polyroots( v)

 

x =

 

2

 

- вектор корней

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

1

Пример. Найти все корни уравнения x3 −10x + 2 = 0

 

 

 

 

2

 

 

 

 

 

 

 

v

 

 

 

 

10

x

 

polyroots( v)

x =

 

 

3.258

 

 

 

 

 

 

 

 

 

 

 

0.201

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.057

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.2. Решение систем уравнений

Пусть необходимо решить систему уравнений

f1 (x1 , x2 ,..., xn ) = 0 f 2 (x1 , x2 ,..., xn ) = 0

........................

f n (x1 , x2 ,..., xn ) = 0

Процедура решения в пакете Mathcad имеет следующий вид.

x1 := x10

 

x2 := x20

- задаются начальные значения для всех

..............

 

xn := xn0

 

переменных системы.

Given - ключевое слово.

f1 (x1 , x2 ,..., xn ) = 0

f 2 (x1 , x2 ,..., xn ) = 0

 

- записываются уравнения системы.

........................

 

f n (x1 , x2 ,..., xn ) = 0

 

V:= Find(x1,x2,...,xn) V= - находится решение системы

уравнений в виде

вектора

значений соответствующих

переменных.

 

Здесь Find(x1,x2,...,xn)

- функция

которая возвращает

решение системы уравнений в виде

вектора значений

соответствующих переменных если оно существует.

При записи системы уравнений, после ключевого слова Given, при необходимости можно указывать ограничения на возможные значения переменных, используя символы £, ³, > и >. При этом недопустимы ограничения со знаком ¹ и неравенства вида a<b<c.

Если система уравнений является нелинейной, то найденное решение может быть не единственным и зависеть от начальных значений переменных.

Пример. Решить систему уравнений:

x 2 − y = 1

x + y = 2

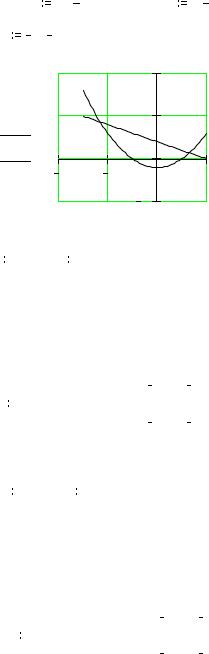
y1( x)

x2

1

y2( x)

2

x

x

3 ,

2.9.. 2

 

 

 

 

 

 

 

10

 

 

y1( x)

 

 

 

5

 

 

 

 

 

 

 

 

y2( x)

 

 

 

 

 

 

 

 

4

2

0

 

2

 

 

 

 

5

 

 

 

 

 

 

x

 

 

Строим графики линий y1(x), y2(x) и определяем примерные координаты точек их пересечения для задания начальных приближений для переменных x и y.

x

 

 

 

 

 

 

2

 

y

 

5

 

- начальные приближения для поиска

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Given

 

 

 

 

 

первого решения

 

 

 

 

 

 

 

 

 

 

 

x2

 

 

 

 

 

y

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

y

 

 

2

 

 

 

 

 

 

2.303

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V

 

 

 

 

 

 

Find( x, y)

V =

 

 

 

 

- найдено первое решение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.303

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

2

 

 

y

 

5

- начальные приближения для поиска

 

 

 

 

 

 

Given

 

 

 

 

второго решения

 

 

 

 

 

 

 

x2

 

 

 

 

y

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

y

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W

 

 

 

 

 

Find( x, y)

W =

 

- найдено второе решение

 

 

 

 

 

1.303

 

 

 

 

 

0.697

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Для решения систем уравнений в пакете Mathcad помимо функции Find(x1,x2,...,xn) предусмотрена еще одна функция Minerr(x1,x2,...,xn). Различие между ними состоит в следующем. Функция Find(x1,x2,...,xn) работает таким образом что, если в результате поиска решения не может быть получено дальнейшее уточнение текущего приближения к решению, она возвращает сообщение об ошибке “ решение не найдено”. Функция Minerr(x1,x2,...,xn) в этом случае возвращает это приближение. Найденное

приближение будет в некотором смысле наилучшим образом удовлетворять уравнениям системы. Если же система уравнений имеет решение, то функция Minerr(x1,x2,...,xn) возвратит тот же результат что и функция Find(x1,x2,...,xn). Пример. Решить систему уравнений:

x 2 + y 2 = 1

( x − 3) 2 + y 2 = 1

Данная система уравнений не имеет точного решения поскольку окружности, определяемые уравнениями системы не пересекаются.

Для поиска приближенного решения воспользуемся функцией Minerr(x1,x2,...,xn)

x

 

 

0

 

 

 

y

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Given

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x2

 

 

 

 

y2

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

( x

 

 

 

3)2

 

 

 

 

y2

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x0

 

 

 

 

 

 

 

Minerr( x, y)

 

x0

 

 

 

 

 

 

 

 

 

 

 

 

=

1.5

 

 

y0

 

 

 

 

 

 

 

 

y0

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

7.215 10

Найдены координаты точки (x0,y0), лежащей на равном расстоянии от каждой из окружностей

Для решения систем линейных уравнений можно наряду с рассмотренным выше способом можно воспользоваться их векторно-матричным представлением.

Пример. Решить систему линейных уравнений:

2x1 + 3x2 − x3 = 5

 

− 4x2

+ x3 = −4

x1

3x + 5x

2

− 2x

3

= 7

 

1

 

 

2 3 1

A 1 4 1

3 5 2

- матрица

 

 

 

 

5

- вектор правых

B

 

 

 

 

 

 

 

 

 

4

частей уравнений

коэффициентов.

 

 

 

 

 

 

 

 

 

 

 

7

системы.

 

 

 

 

 

В матричной записи исходная система принимает: AX=B

 

1

 

X

 

A 1 .B X =

2

- найден вектор решений.

 

 

 

3

 

1.Дифференциальные уравнения и системы

1.1. Дифференциальные уравнения и системы первого порядка

Рассмотрим дифференциальное уравнение(ДУ) первого порядка

dy = f ( x, y) dx

Для решения этого уравнения можно воспользоваться известными методами Эйлера, Рунге-Кутта или использовать встроенные функции пакета Mathcad.

Пример. Выполнить численное интегрирование методом Эйлера дифференциального уравнения:

dy + 2xy = 2x 2 sin x dx

при начальном условии y(0)=1 на отрезке x [0,2] с шагом

0,2.

Запишем исходное уравнение в виде:

dy = −2xy + 2x 2 sin x dx

Реализация алгоритма метода Эйлера в пакете Mathcad может иметь вид

f( x, y)

 

2.x.y

2.x2 .sin( x)

x

0

 

y

1

 

 

 

 

 

 

 

 

 

 

 

0

 

 

0

 

 

 

 

 

x1

0

h

0.2

 

N

20

 

 

 

 

 

 

 

 

 

i 1 .. N

 

x

x

1

h

y

y

1

h.f x

1

, y

1

 

 

 

 

i

i

 

i

i

 

i

i

 

 

 

 

2

 

 

 

 

 

 

 

 

 

График зависимости

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

yi

y xi

 

yi

 

0

 

1

 

2

 

3

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xi

 

 

 

 

 

 

 

 

 

 

 

 

дискретные значения решения y=y(x)

 

В пакете Mathcad для решения ДУ и систем ДУ вида

dy

0

 

=

f0 (x, y0 , y1 ,..., yn )

 

 

 

 

 

 

dx

 

 

dy1

=

 

 

 

 

 

f1 (x, y0 , y1 ,..., yn )

 

 

 

dx

 

 

.......................................

 

 

 

 

 

 

 

 

dyn

= f

 

(x, y

 

, y ,..., y

 

)

 

 

n

0

n

 

 

1

 

dx

 

 

 

 

 

 

 

существует встроенная функция

rkfixed(V,x1,x2,Npoints,D), где

V- вектор начальных условий размерности n (n - порядок ДУ или число уравнений в системе);

x1,x2 - граничные точки интервала на котором ищется решение дифференциальных уравнений (начальные условия, заданные в векторе V, -это значение решения в точке x1;

Npoints - число точек ( не считая начальной точки ), в которой ищется решение;

D(x,V)- функция, которая возвращает значение в виде вектора из n элементов, содержащих первые производные неизвестных функций.

Функция rkfixed возвращает матрицу первый столбец которой содержит точки в которых ищется решение, второй столбец содержит значения найденного решения в соответствующих точках для первого уравнения системы, второй столбец - для второго уравнения системы и т.д. Пример1. Выполнить численное интегрирование дифференциального уравнения:

dy = y cos x + 2 sin 2x dx

при начальном условии y(0)=1 на отрезке x [0,1]

x1

0

x2

2

 

 

- граничные точки интервала на котором

 

 

 

 

 

 

ищется решение.

 

y

1

 

 

 

 

- начальное значение функции y(x): y

y( x1) .

0

 

 

 

 

 

 

0

 

Np

20

 

 

 

 

- число точек в которых ищется решение.

 

 

 

 

 

 

 

D( x, y)

y.cos( x)

2.sin( 2.x)

- в этом выражении y есть вектор

 

 

 

 

 

 

 

начальных условий, содержащий

 

 

 

 

 

 

 

один элемент y .

 

 

 

 

 

 

 

 

0

 

Z rkfixed( y, x1, x2, Np , D)

- матрица, столбцы которой содержат

 

 

 

 

 

 

 

дискретный набор значений

 

 

 

 

 

 

 

аргумента и искомой функции.

 

N

length( Z<0 > )

1

i

1 .. N

 

 

 

6

 

 

 

 

 

Z<0 > -дискретный набор

 

 

 

 

 

 

 

 

 

 

 

 

 

 

значений аргумента x,

 

 

4

 

 

 

 

 

Z<1 > -дискретный набор

Z<1 >

 

 

 

 

 

 

i

 

 

 

 

 

значений функции y

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

0

0.5

1

 

1.5

2

 

 

 

 

 

Z<0

>

 

 

 

 

 

 

 

 

i

 

 

 

 

 

 

дискретные значения решения y=y(x)

 

Пример2. Выполнить численное интегрирование дифференциального уравнения:

dy = x cos y + 2 sin 2 y dx

при начальном условии y(0)=1 на отрезке x [0,1]

x1

0

x2

2

 

 

- граничные точки интервала на котором

 

 

 

 

 

 

ищется решение.

y

1

 

 

 

 

- начальное условие для функции y(x).

0

 

 

 

 

 

 

 

Np

20

 

 

 

 

- число точек в которых ищется решение.

 

 

 

 

 

 

D( x, y)

x.cos( y)

 

2.sin( 2.y)

- поскольку здесь y- вектор, то

 

 

 

 

 

 

необходимо использовать

 

 

 

 

 

 

оператор векторизации.

Z

rkfixed( y, x1, x2, Np , D)

- матрица, столбцы которой содержат

 

 

 

 

 

 

дискретный набор значений

 

 

 

 

 

 

аргумента и искомой функции.

N

length( Z<0 > )

1

i

1 .. N

 

 

1.6

 

 

 

 

 

Z<0 > -дискретный набор

 

 

 

 

 

 

 

 

 

 

 

 

 

 

значений аргумента x,

 

1.4

 

 

 

 

 

Z<1 > -дискретный набор

Z<1 >

 

 

 

 

 

 

i

 

 

 

 

 

значений функции y

 

 

 

 

 

 

 

 

1.2

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

0

0.5

 

1

1.5

2

 

 

 

 

 

Z<0 >

 

 

 

 

 

 

 

i

 

 

 

 

 

дискретные значения решения y=y(x)

Пример3. Выполнить численное интегрирование системы дифференциальных уравнений:

dy

0

 

= y1 + 1

 

 

 

 

 

 

dx

 

dy1

= − y0 − 1

 

 

 

 

dx

 

при начальных условиях y0(0)=1 y1(0)=1 на отрезке x [0,15]

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности