
метода, MCad6
.0.pdf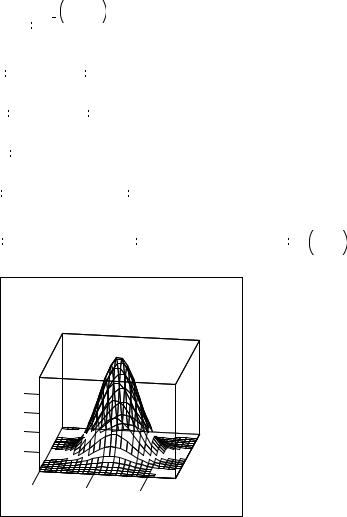
f( x, y) |
|
e |
x2 |
|
|
|
|
y2 |
Определение функции |
|||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
2.5 |
y0 |
|
|
|
|
|
|
2.5 |
Начальные значения аргументов |
|||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||
x |
|
|
0.2 |
y |
|
|
0.2 |
Шаг изменения аргументов |
||||||||||||
|
|
|
||||||||||||||||||
N |
|
26 |
|
|
|
|
|
|
|
|
|
|
|
Число точек на осях X и Y |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
i |
|
|
0 .. N |
|
|
1 |
x |
|
|
x0 |
|
|
|
|
i. x |
|
|
|
|||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
0 .. N |
|
1 |
y |
|
|
|
y0 |
|
|
j. y |
M |
|
f x , y |
|||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
i, j |
|
i j |
Пример графика поверхности
0.8
0.6
0.4










 0
0
0.2

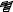

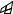


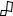
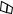



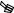

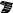

 10
10



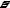
 20
20
0 |
10 |
20 |
M
2.2.Форматирование 3-х мерного графика
Для форматирования |
3-х мерного графика |
необходимо: |
|
∙выделить график щелчком ЛКМ;
∙выполнить команду меню Graphics/3D Plot Format (
Графики/ Формат 3D графики);
После этого появится окно "Формат 3D графики", содержащее четыре вкладки, позволяющие выполнять форматирование отдельных элементов графика:
♦ View(Вид) - позволяет выполнить вращение ( Rotation ) графика, изменять угол наклона относительно плоскости х-y под которым виден график( Titl ) и другие операции
♦Axes(Оси) - позволяет установить линии сетки по осям координат;
♦Color & Lines (Цвет) - изменяет цвет окраски графика;
♦Title(Заголовок) - позволяет задать название графика.
2.3.Построение карты линий уровня функции 2-х переменных
∙ рассчитать матрицу |
значений |
функции |
f(x,y): |
Mi,j=f(xi,yi) на заданном множестве значений |
(xi, yi) |
||
аргументов x и y. |
|
|
|
∙выполнить команду меню Graphics/Create Contour Plot
(Графики/создать карту линий уровня) и в поле ввода шаблона напечатать имя матрицы, содержащей значения функции.
После заполнения поля шаблона необходимо щелкнуть ЛКМ вне области графика при работе в автоматическом режиме или нажать клавишу F9 при работе в ручном режиме. Карта линий уровня будет отображена на экране.
Для изменения размеров карты, ее необходимо выделить пунктирной линией и изменить размер, ухватившись мышью за правую или нижнюю границу выделенной области ( при этом курсор должен принять вид двойной стрелки).
Пример. График поверхности и карта линий уровня для функции f (x, y) = x2 − y2

|
График поверхности |
|
5 |
|
|
0 |
|
0 |
|
|
|
5 |
|
10 |
|
20 |
|
|
|
|
0 |
10 |
20 |
M |
|
|
|
|
Карта линий уровня |
|||||
2 |
2 1 0 |
1 |
2 |
3 |
|
1 2 |
|
|
2 |
||||||
1 |
4 |
|
|
|
1 |
0 |
4 |
|
|
|
|
|
|
||
|
|
3 |
|
|
0 |
|
3 |
0 |
|
|
2 |
|
|
2 |
|
|
|
1 |
0 |
1 |
|||
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
||
1 |
4 |
|
|
|
1 |
0 |
4 |
3 |
|
|
|
3 |
|||
|
|
|
|
|
2 |
||
|
2 1 |
0 |
1 |
2 |
3 |
1 2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
1 |
0 |
1 |
2 |
|
M |
|
|
|
|
|
|
|
Карта линий уровня строится таким образом, что ось X графика идет направо, а ось Y направлена вверх. Так как карта линий уровня создается помещением значений функции в матрицу, Mathcad не знает истинных значений x и y. По этой причине на карте линий уровня по умолчанию нормированы так, что координаты изменяются от -1 до 1. Если необходимо установить истинные границы изменения аргументов x и y, то необходимо выполнить команду меню
Graphics/3D Plot Format ( Графики/ Формат 3D графики),
выбрать вкладку Axes(Оси) и на ней заполнить поля Min.Val. ( Мин. Знач.) и Max. Val.( Макс. Знач.) необходимыми значениями для X- оси (X- Axis) и Y- оси (Y- Axis).
2.4.Форматирование карты линий уровня
Форматирование карты линий уровня выполняется аналогично форматированию 3-х мерного графика. Используется команда меню Graphics / 3D Plot Format.
Замечание: Функция двух переменных f(x,y) может быть графически представлена либо в виде графика поверхности либо в виде карты линий уровня. Переключение между этими формами представления, производится по вкладке View( Вид ) в окне “ Формат 3D графика”. Кнопка Surface Plot -устанавливает отображение графика в виде
поверхности, а кнопка Countaur Plot - в виде карты линий уровня.
1.Вычисления в пакете Mathcad
1.1.Операции с матрицами и векторами.
Для проведения вычислений с матрицами и векторами в пакете Mathcad предусмотрен ряд встроенных функций. Ниже приведены некоторые из них.
Имя |
Возвращается... |
функции |
|
rows(A) |
Число строк в массиве A. Если A - скаляр, |
|
возвращается 0. |
cols(A) |
Число столбцов в массиве A. Если A - скаляр, |
|
возвращается 0 |
lenght(v) |
Число элементов в векторе v |
last(v) |
Индекс последнего элемента в векторе v |
max(A) |
Максимальный элемент в массиве A |
min(A) |
Минимальный элемент в массиве A |
identity(n) |
(n×n)- единичная матрица |
diag(v) |
Диагональная матрица, содержащая на |
|
диагонали элементы вектора v |
tr(A) |
Сумма диагональных элементов матрицы A |
|
(след A ). Матрица A должна быть |
|
квадратной |
Рассмотрим примеры некоторых операций с матрицами и векторами.

Произведение матриц
|
|
|
1 |
|
3 |
6 |
|
|
|
|
|
|
2 |
5 |
|
7 |
|
|
|
|
|
|
68 |
32 |
|
31 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
A |
|
|
7 8 2 |
|
|
|
B |
|
|
4 5 6 |
|
C |
|
A.B C = |
64 79 |
99 |
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
7 |
|
5 |
4 |
|
|
|
|
|
|
9 |
2 |
|
1 |
|
|
|
|
|
|
70 |
68 |
|
83 |
|
|
|
||||
Произведение матрицы на вектор |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
59 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
5 |
|
|
D |
|
|
|
A.V |
D = |
|
|
68 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
67 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Транспонирование матрицы и вектора |
Вычисление определителя |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
матрицы |
|
|
|
|
|
|
||||
AT = |
|
1 |
7 |
7 |
|
|
|
VT = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
3 |
8 |
5 |
|
|
|
|
2 |
|
5 7 |
|
|
|
|
D |
|
|
A |
|
|
D = |
|
146 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
6 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисление обратной матрицы
A 1 = |
|
|
0.151 |
|
0.123 |
0.288 |
A 1 .A = |
1 |
0 |
0 |
|
|
|
||||||||||
0.096 |
0.26 |
|
0.274 |
0 |
1 |
0 |
|||||
|
|||||||||||
|
0.144 |
|
0.11 |
0.089 |
|
0 |
0 |
1 |
|||
|
|||||||||||
Скалярное произведение векторов
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
|
|
|
3 |
|
|
s |
|
|
|
W.V |
s = 52 |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
V |
|
d = |
8.832 |
- длина вектора V |
||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
- определитель матрицы A |
|||||||
d |
|
|
|
|
|
|
A |
|
d = |
|
|
146 |
|||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|||||||||||||||||
s |
|
|
|
|
|
V |
s = |
14 |
|
- сумма элементов вектора V. |
|||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
A< 0 > |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||
Y |
|
|
Y = |
7 |
- первый столбец матрицы A |
||||||||||||||
|
|
|
|
||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|||

Число строк и столбцов матрицы A
n |
|
|
|
|
|
rows( A) |
n = 3 |
|
m |
|
|
|
|
cols( A) m = 3 |
||||
|
|
|
|
|
|
|
||||||||||||
max( B) = 9 |
min( B) = |
1 |
|
|
|
|||||||||||||
k |
|
|
|
|
|
length( V) |
k = |
3 |
|
|
|
|
- число элементов вектора V |
|||||
|
|
|
|
|
|
|
|
|||||||||||
m |
|
|
|
|
|
last( V) |
m = |
2 |
|
|
|
|
- индекс последнего элемента в векторе V |
|||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
|
|
|
|
- создана единичная матрица |
|
I |
|
|
|
|
|
|
identity( 2) |
I = |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
T |
|
|
|
|
|
diag( V) |
T = |
|
0 |
5 |
|
0 |
|
|
- создана диагональная матрица с |
|||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
7 |
|
|
элементами вектора V на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
диагонали |
p |
|
|
|
|
|
tr( B) |
p = 8 |
|
|
|
|
|
|
- след матрицы B |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для выполнения поэлементных операций над элементами векторов или матриц в пакете Mathcad существует оператор векторизации, который предписывает Mathcad применять операторы и функции к каждому элементу массива поочередно. Так если V- вектор, то sin(V)- недопустимое выражение. Но если использовать оператор векторизации, Mathcad вычисляет синус каждого элемента вектора V, а результат - новый вектор, чьи элементы - синусы элементов
V.
Для применения оператора векторизации к некоторому выражению необходимо заключить это выражение в выделяющую рамку и нажать комбинацию клавиш “ Ctrl” и” −”. Сверху выделенного выражения будет помещена стрелка. Например
|
|
|
1 |
|
|
|
0.841 |
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
V2 = |
|||||
V |
|
|
2 |
|
sin( V) = |
0.909 |
|
4 |
|||
|
|
||||||||||
|
|||||||||||
|
|
|
3 |
|
0.141 |
|
9 |
||||
1.2. Простейшие вычисления в пакете
Mathcad
Ниже приведены примеры простейших вычислений в математическом пакете Mathcad. Сюда относятся вычисление
алгебраических выражений, сумм, произведений, интегралов, производных, логических выражений и т. д.
Напомним, что нужный математический оператор может быть введен нажатием соответствующей комбинации клавиш на клавиатуре или взят из палитры символов.

|
|
|
|
|
|
|
sin( x) |
|
|
|
|
|
ln( y) |
|
|
x |
|
0.5 y |
|
6.7 z |
|
|
|
|
|
|
|
|
|
z = 9.783 109 |
- вычисление значения |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
e x2 |
|
|
|
|
|
y2 |
алгебраического |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выражения |
f( x) |
|
|
x.ex |
|
|
|
2.ln( x |
|
|
|
1) |
- определение функции |
|||||||
|
|
|
|
|
|
|
|
||||||||||||
I |
|
|
|
5 |
|
|
f( x) dx |
|
|
|
I = 604.381 |
- вычисление интеграла |
|||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
F( t , a) |
|
|
|
|
|
|
|
|
- определение функции |
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
f( x) dx |
||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
F( 5 , 1) = 604.381 - предыдущий пример с использованием функции F(t,a)
x |
|
|
|
0 |
|
|
|
|
|
|
|
p |
|
|
d |
|
|
f( x) |
p = 3 |
|
|
- производная функции f(x) при x=0 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
P( x) |
|
|
d |
|
f( x) |
|
|
|
|
|
|
- определение функции |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
d x |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
P( 0) = 3 |
|
|
|
|
|
|
- предыдущий пример с использованием функции P(x) |
||||||||||||||||||||||||||||||||||||||||||
i |
|
|
1 , 3 .. 7 |
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
i |
s = 16 |
|
- сумма нечетных чисел на отрезке [1,7] |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
i |
|
|
2 , 4 .. 10 |
|
|
p |
|
|
|
|
|
|
|
|
|
i2 |
p = 1.475 107 |
- произведение квадратов четных |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чисел на отрезке [2,10] |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
1 |
s = 6 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
V |
|
|
|
|
2 |
|
|
|
|
|
|
n |
|
|
length( V) s |
|
|
|
|
|
Vi |
|
- сумма элементов |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = 0 |
|
|
|
вектора V |
|||||||||||
|
|
|
|
|
|
|
|
n |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p = 6 |
|
|
|
|
|
|
|
|
|
|
||||||||
p |
|
|
|
|
|
|
|
|
|
Vi |
|
|
|
|
|
|
|
|
- произведение элементов вектора V |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 , x2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 , x |
|
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
f( x) |
|
|
if x |
|
|
|
|
|
x |
- определение функции f( x) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
x , x> 0 |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f( |
|
3) = 9 |
|
|
|
|
|
|
f( 9) = 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1.Алгебраические уравненения и системы
1.1. Решение одного уравнения
Для решения одного уравнения с одним неизвестным f(x)=0 в пакете Mathcad используется функция root(f(x),x), где f(x)- функция, определенная где-либо в рабочем документе, или выражение, которое возвращает скалярное значение,
x - имя переменной, относительно которой ищется решение уравнения.
Функция root(f(x),x) возвращает значение x при котором f(x)=0. Для нахождения корня Mathcad использует численный метод. Поэтому перед использованием функции root(f(x),x) переменной x необходимо присвоить начальное значение. Если функция f(x) имеет несколько корней, то найденное значение корня будет зависеть от начального приближения для переменной x. Будет найдено то значение корня, в окрестности которого задано начальное приближение.
Пример. Найти все корни уравнения e−x cos( x) = 0.5 на отрезке
[-1.5, 1.5]
|
f( x) |
e x.cos( x) |
0.5 |
x |
1.5, 1.4.. 1.5 |
|||
|
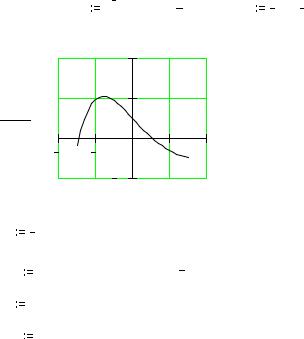
График функции f(x) |
Строим график функции f(x) на |
||||||
|
|
|
2 |
|
|
|
заданном отрезке и определяем |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
примерное положение корней |
|
f( x) |
|
|
1 |
|
|
|
на оси X . |
|
|
|
|
|
|
|
|||
|
2 |
|
1 |
0 |
1 |
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
1 |
- начальное приближение для первого корня. |
||||||
x1 |
root( f( x) , x) |
|
x1 = |
1.454 |
|
- найден первый корень. |
||
x |
1 |
- начальное приближение для второго корня. |
||||||
x2 |
root( f( x) , x) |
|
x2 = 0.54 |
|
- найден второй корень. |
|||
