
метода, MCad6
.0.pdf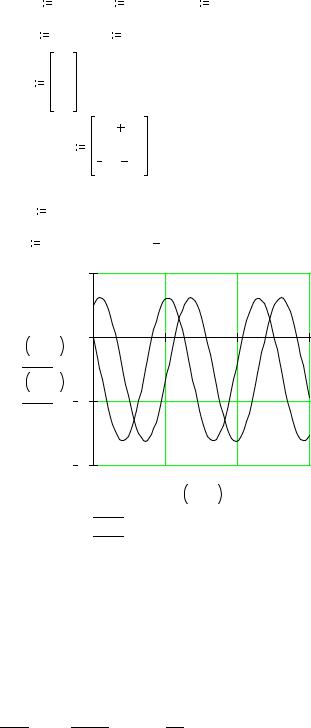
x1 |
0 |
x2 |
15 |
Np |
|
100 |
|
|
||
y |
|
1 |
y |
0 |
|
- начальные условия |
|
|||
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
y |
|
0 |
|
|
|
-вектор начльных условий |
|
|||
|
y |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
y |
1 |
|
|
|
|
|
|
D( x, y) |
1 |
|
|
- вектор правых частей системы ДУ |
|
|||||
y |
1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
|
|
|
Z rkfixed( y, x1, x2, Np , D) |
- решение на отрезке [ x1,x2 ] в Np точках |
|
||||||||
i |
0 .. length( Z<0 > ) |
1 |
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
Z<0 > -дискретный набор |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
значений аргумента x, |
|
|
Z<1 > |
|
|
|
|
|
|
Z<1 > -дискретный набор |
||
|
|
i |
0 |
|
5 |
|
|
10 |
15 |
( x) |
|
Z<2 > |
|
|
|
|
|
|
значений функции y |
||
|
|
|
|
|
|
|
0 |
|
||
|
|
|
|
|
|
|
|
|
||
|
|
i |
|
|
|
|
|
|
Z<2 > - дискретный набор |
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
значений функции y |
( x) |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Z<0 > |
|
|
||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
y0(x) |
|
|
|
|
|
|
|
|
|
|
y1(x) |
|
|
|
|
|
|
|
1.2. |
Дифференциальные уравнения высокого |
|
|||||||
|
|
|
|
|
|
|
|
|
порядка |
|
Рассмотрим дифференциальное уравнение n-го порядка |
|
|||||||||
d n y |
+ a |
d n−1 y + ... + a |
dy + a |
|
y = 0 |
|
|
|||
dx n |
|
n−1 dx n−1 |
1 dx |
|
0 |
|
|
|
||
с начальными условиями |
|
|
|
|
||||||

y(x0 ) = y0
′ |
′ |
y (x0 ) = y |
0 |
′′ |
′′ |
y (x0 ) = y0 |
|
................. |
|
y n−1 (x0 ) = y0 n−1
Процедура решения такого ДУ в пакете Mathcad сводится к решению рассмотренной выше системы ДУ. Для этого введем обозначения:
y = y0
′ |
= y1 |
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
||
′′ |
|
′ |
= y2 |
|
|
|
|
|
y0 |
= y1 |
|
|
|
|
|
||
′′′ |
|
′ |
= y3 |
|
|
|
|
|
y0 |
= y2 |
|
|
|
|
|||
.................... |
|
|
|
|
|
|||
n−1 |
|
′ |
= yn−1 |
|
|
|||
y0 |
|
|
|
|
||||
|
= yn−2 |
|
|
|||||
n |
= −an−1 y |
n−1 |
− an−2 y |
n−2 |
′ |
|||
y0 |
|
|
− ... − a0 y = −an−1 yn−1 − an−2 yn−2 − ... − a0 y0 = yn−1 |
|||||
Таким образом имеем систему уравнений
y |
′ |
= y |
|
|
|
|
|
|
||
|
|
0 |
|
1 |
|
|
|
|
|
|
|
′ |
= y2 |
|
|
|
|
|
|
||
y1 |
|
|
|
|
|
|
||||
|
|
′ |
= y3 |
|
|
|
|
|
|
|
y |
2 |
|
|
|
|
|
|
|||
.................... |
|
|
|
|
|
|
||||
|
|
′ |
|
|
|
|
|
|
|
|
|
|
−2 |
= yn−1 |
|
|
|
|
|
|
|
|
yn |
|
|
|
|
|
|
|||
|
′ |
|
= −an−1 y |
n−1 |
− an−2 y |
n−2 |
− ... − a0 y = −an−1 yn−1 |
− an−2 yn−2 |
− ... − a0 y0 |
|
|
|
|
||||||||
yn−1 |
|
|
||||||||
и систему начальных условий
y |
0 |
(x |
0 |
) = y |
0 |
= y |
00 |
|
|
|
|
|
|||||
|
|
|
|
′ |
= y10 |
|||
y1 (x0 ) = y0 |
||||||||
|
|
|
|
|
′′ |
|
|
|
y2 (x0 ) = y |
= y20 |
|||||||
0 |
||||||||
.......................... |
||||||||
|
|
|
|
|
|
n−1 |
|
|
|
|
−1 (x0 ) = y |
= yn−1,0 |
|||||
yn |
0 |
|||||||
Пример. Решить дифференциальное уравнение
d 2 y + 2 dy + 17 y = 0 , dx 2 dx
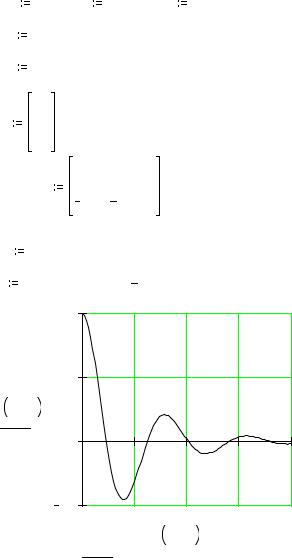
для начальных условий |
y(0) = 1, y′(0) = 0 при x [0,4] |
||||||||||
В соответствии с вышеизложенным положим |
|||||||||||
y = y0 |
|
|
|
|
|
|
|
|
|
|
|
|
y ′ = y |
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
y ′ = −2 y |
1 |
− 17 y |
0 |
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
||
Тогда решение задачи в пакете Mathcad будет иметь |
|||||||||||
следующий вид. |
|
|
|
|
|
|
|||||
|
x1 |
0 |
|
x2 |
|
4 |
|
Np |
|
100 |
|
|
y |
1 |
|
- начальное условие для функции y(x) |
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
- начальное условие для производной y'(x) |
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
y |
0 |
|
|
|
|
-вектор начльных условий |
||||
|
y |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
- первая производная функции y(x) |
||
|
D( x, y) |
|
|
1 |
|
|
|
|
|
||
|
2.y |
|
17.y |
- вторая производная функции y(x) |
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
Z |
rkfixed( y, x1, x2, Np , D) |
- решение на отрезке [ x1,x2 ] в Np точках |
||||||||
|
i |
0 .. length( Z<0 > ) |
1 |
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
Z<0 > -дискретный набор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значений аргумента x, |
|
Z<1 > |
|
0.5 |
|
|
|
|
|
|
Z<1 > -дискретный набор |
|
|
|
|
|
|
|
|
|
|
значений функции |
||
|
|
i |
|
|
|
|
|
|
|
y ( x) =y(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
0 |
|
|
1 |
2 |
3 |
4 |
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z<0 > |
|
||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
y(x) |
|
|
|
|
1.Статистический анализ
Для решения задач статистического анализа в пакете Mathcad предусмотрен ряд встроенных функций, позволяющих получить статистические оценки случайных совокупностей. Ниже приводится их описание. При этом предполагается, что m- число строк, а n- число столбцов в рассматриваемых массивах.
mean(A) Возвращает среднее значение элементов массива A размерности m×n
согласно формуле mean( A) = |
1 |
m−1 n−1 |
|
∑∑ Ai, j . Если V- |
|||
|
mn i=0 j=0
вектор (n=1), то
1 m−1
mean(V ) = ∑Vi m i=0
var(A) Возвращает дисперсию элементов массива A размерности m×n
|
1 |
m−1 n−1 |
|
|
|
|
|
|
||||
согласно формуле var(A) = |
∑∑ |
|
Ai, j − mean( A) |
2 |
|
|
||||||
|
|
|
|
|
||||||||
|
mn i=0 j =0 |
|
|
|
|
|
|
|
|
|||
|
|
m−1 |
||||||||||
|
|
|
1 |
|||||||||
Если V- вектор (n=1), то var(V ) = |
∑ |
|
Vi − mean(V ) |
|
2 |
|||||||
|
|
|||||||||||
|
||||||||||||
|
|
|
m i=1 |
|
|
|
|
|||||
cvar(A,B) Возвращает ковариацию элементов массивов A и B размерности m×n
согласно формуле
c var(A, B) = 1 |
m−1 n−1 |
∑∑[ Ai, j − mean( A)][Bi, j − mean(B)] , где |
mn i=0 j =0
черта означает комплексное сопряжение. Если A и B вектора с действительными элементами, то
c var(V ,W ) = 1 |
m−1 |
∑[Vi − mean(V )][Wi − mean(W )] |
m i=0
stdev(A) Возвращает среднеквадратичное отклонение ( квадратный корень из дисперсии ) элементов m×n массива A
corr(A,B) Возвращает скаляр: коэффициент корреляции для двух m×n массивов A и B
Mathcad содержит ряд встроенных функций для генерирования случайных чисел, имеющих разнообразные распределения вероятностей.
rnorm(N,m,σ) Возвращает вектор N случайных чисел, имеющих нормальное распределение с математическим ожиданием m и среднеквадратичным отклонением σ (квадратный корень из дисперсии).
runif(N,a,b) Возвращает вектор N случайных чисел, имеющих равномерное распределение на отрезке [а,b], a<b.
rnd(x) Возвращает равномерно распределенное случайное число на отрезке [0,1]. Эквивалент runif(1,0,x).
Mathcad содержит встроенную функцию hist для вычисления частотного распределения, применяемого для построения гистограмм.
hist(int,A) - возвращает вектор, представляющий частоты, с которыми величины, содержащиеся в векторе А , попадают в интервалы, представляемые вектором int. Элементы в А и int должны быть вещественными. Кроме того, элементы int должны быть расположены в порядке возрастания. Возвращаемый результат - вектор, содержащий на один элемент меньше, чем int.
Пример. Получить выборку размером N=100 элементов из последовательности случайных чисел, имеющих нормальное распределение, математическое ожидание a=5 и среднеквадратичное отклонение σ=1. Определить для нее среднее значение, дисперсию, среднеквадратичное отклонение и построить гистограмму.

a |
|
|
5 |
|
|
|
|
σ |
|
1 |
|
|
|
|
N |
|
|
|||||||
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
VS |
|
|
|
|
rnorm( N , a , σ) |
|||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
m |
|
|
|
|
|
|
1 . |
N |
|
|
1 |
VSi |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
N |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = 0 |
||||||||||
|
|
|
|
|
|
|
|
|
1 . |
N |
|
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ds |
|
|
|
|
|
|
|
|
|
VSi |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
N |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i = 0 |
|||||||||
sd |
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
100 |
- параметры для создания выборки |
- вектор случайных чисел
m = 4.85 - среднее значение выборки
m 2 |
ds = 0.955 |
- дисперсия выборки |
sd = 0.977 - среднеквадратичное отклонение
Те же операции с использованием встроенных функций Mathcad
m |
|
|
|
mean( VS) |
|
|
m = 4.85 |
|
- среднее значение выборки |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
ds |
|
|
|
var( VS) |
|
|
ds = 0.955 |
|
- дисперсия выборки |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
sd |
|
|
|
stdev( VS) |
|
|
sd = 0.977 |
|
- среднеквадратичное отклонение |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Построение гистограммы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
δ |
|
|
|
0.25 |
|
|
|
|
|
|
|
|
|
|
|
|
- ширина интервалов, набор которых будет |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
содержать вектор Int |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
0 .. 24 Inti |
|
2 |
|
i δ |
|
формирование вектора интервалов |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
f |
|
|
|
hist( Int, VS) |
|
|
|
|
|
|
|
|
|
|
- формирование вектора частот |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
i |
|
|
|
0 .. length( Int) |
|
|
2 |
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
fi |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
Inti |
6 |
|
|
|
|
|
|
|
8 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1.Функции регрессии
Mathcad включает ряд встроенных функций, позволяющих получить уравнение регрессии по набору экспериментальных данных. Эти функции создают кривую определенного типа, которая в некотором смысле минимизирует ошибку между собой и имеющимися данными. Они отличаются между собой прежде всего типом кривой, которую они используют для аппроксимации данных. Рассмотрим некоторые из этих функций.
1.1. Линейная регрессия
Уравнение регрессии в пакете Mathcad можно представить в виде:
y(x)=slope(VX,VY)*x+intersept(VX,VY),
где VXвектор измеренных значений аргумента , VY - вектор измеренных значений функции. Функция наилучшим образом приближает данные в смысле наименьших квадратов.
Пример. По заданному набору экспериментальных данных получить уравнение регрессии в виде линейной функции.
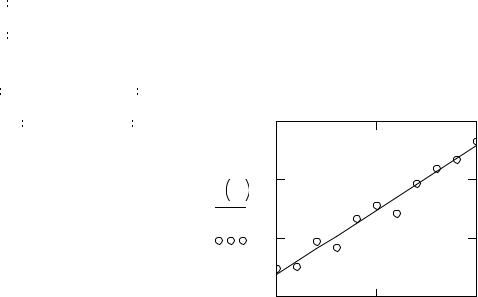
Линейная регрессия: |
y(x)=a.x |
|
|
|
b |
|
|||||
|
|
|
|
||||||||
vx |
|
( 0 |
1 2 |
3 4 |
5 |
6 7 8 9 10 )T |
- значения аргумента |
||||
|
|||||||||||
|
|||||||||||
vy |
|
( 2.5 |
2.6 |
4.8 |
4.3 |
6.7 7.8 7.2 |
9.7 11 11.8 13.3 )T |
- измеренные значения |
|||
|
|||||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
функции |
a |
|
slope( vx, vy) |
b |
|
intercept( vx, vy) |
|||||||
|
|
|||||||||||
|
|
|||||||||||
y( x) |
|
a.x |
|
|
|
b |
i |
|
0 .. 10 |
|||
|
|
|
|
|
||||||||
y vxi
vy i
15 |
|
|
10 |
|
|
5 |
|
|
0 |
|
|
0 |
5 |
10 |
vxi
1.2. Полиномиальная регрессия
Для получения уравнения регрессии в виде полинома
y(x) = a0 + a1 x +... + an x n , ( n ≤ 4)
в пакете Mathcad предусмотрена две функция regress и interp, которые используются совместно.
regress(VX,VY,n) - возвращает вектор, требуемый interp,
чтобы найти полином порядка n, который наилучшим образом приближает данные из VX и VY. VX - есть m - мерный вектор, содержащий координаты x. VY - есть m - мерный вектор, содержащий координаты y, соответствующие m точкам, определенным в
VX.
interp(VS,VX,VY,x) - возвращает интерполируемое значение y, соответствующее x. Вектор VS вычисляется функцией regress ( или loess, см. ниже ) на основе данных из VX и VY.
Функцию regress удобно использовать, когда все данные можно приблизить единственным полиномом. Если же данные не связаны единой полиномиальной зависимостью, то для получения лучшего результата вместо функции regress совместно с interp можно воспользоваться функцией loess, которая выполняет локальное квадратичное приближение данных. Это означает, что вместо одного полинома, как это делает regres, loess создает различные полиномы второго порядка в зависимости от расположения на кривой.
loess(VX,VY,span) - возвращает вектор, требуемый interp,
чтобы найти набор полиномов второго порядка, которые наилучшим образом приближают определенные окрестности выборочных точек, определенных в векторах VX и VY. Вектора VX и VY имеют тот же смысл, что и в функции regress. Аргумент span ( span>0, хорошее значение по умолчанию - span=0.75 ) определяет насколько большие окрестности loess будет использовать при выполнении локального приближения.
Пример. Величины X и Y связаны функциональной зависимостью
x, x ≤ 4 |
||
y(x)= x3 |
, x > 4 |
|
|
|
|
|
||
100 |
|
|
Измерения величины Y производится с погрешностью, которая представляет собой равномерно распределенную на отрезке [ 0,1 ] случайную величину, имеющую среднее значение равное нулю и дисперсию равную 4. Необходимо смоделировать набор измеренных значений величины Y, при условии, что величина X принимает ряд значений в диапазоне от 0 до 10 с шагом равным 1, и получить уравнение регрессии по этим данным.

f( x) |
|
|
|
if |
x |
|
4 , x, |
x3 |
|
- определение функциональной зависимости |
||
|
|
|
|
100 |
||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
N |
|
|
11 |
|
|
- число измерений |
||||||
|
|
|
|
|||||||||
|
|
|
||||||||||
disp |
|
|
4 |
|
|
- дисперсия ошибки измерений |
||||||
|
|
|
|
|||||||||
|
|
|
||||||||||
i |
|
|
|
0 .. N |
|
|
1 |
|
|
|
|
- формирование значений величины X |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
vxi |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
vy |
|
|
|
|
|
|
f( i) |
|
|
|
|
disp.rnd( 1) |
- формирование набора измеренных значений |
|||||||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величины Y |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
vxT = |
|
0 1 2 3 4 5 6 7 8 9 10 |
|
|
|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
vyT = |
|
|
|
|
1.2 2 |
4.1 |
5.2 |
1.6 3.1 3.5 6.7 8.3 11.8 |
|
|||||||||||||||||||
|
|
2 |
|
|||||||||||||||||||||||||
k |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- степень полинома для функции regress |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
span |
|
0.75 |
|
|
|
|
- параметр для функции loess |
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
vs |
|
|
|
|
loess( vx, vy, span) |
|
- вектор, используемый функцией loess |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
y( x) |
|
|
|
|
interp( vs, vx, vy, x) |
- уравнение регрессии при использовании |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
локального квадратичного приближения |
|||
vs1 |
|
|
|
|
|
|
|
|
regress( vx, vy, k) |
|
- вектор, используемый функцией regress |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
y1( x) |
|
|
|
|
|
interp( vs1, vx, vx, x) |
- уравнение регрессии при использовании |
|||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
полинома второго порядка |
|||
i |
|
|
|
|
|
0 .. length( vx) |
|
1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
15 |
|
|
y |
vxi |
10 |
|
|
|
|
|
|
|
|
|
y1 |
|
vxi |
|
|
|
vyi |
|
5 |
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
5 |
10 |
|
|
|
|
vxi |
|
Из графика видно, что в данном случае наилучшее приближение к экспериментальным данным получается с использованием локального квадратичного приближения.
