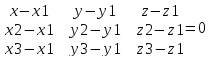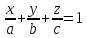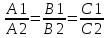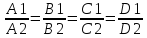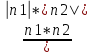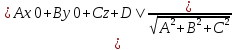- •2.Определение предела ф-ции на языке окрестностей:
- •3.Теорема о локальной ограниченности функции, имеющей при конечный предел
- •4.Функция называется бесконечно малой
- •5.Функция называется бесконечно большой
- •8.Понятие непрерывности функции на промежутке.
- •9.Асимптотой графика функции называется
- •12. Произв сложн ф-и
- •13. Производная обратной функции равна
- •16.Теорема Ферма.Геометрический смысл теоремы Ферма.
- •17.Теорема Ролля.Геометрический смысл теоремы Роля.
- •18.Теоремы Лагранжа и Коши.Геометрический смысл теоремы Лагранжа.
- •19.Правило Лопиталя
- •20.Сравнение роста показательной,степенной и логарифмической функций.
- •22.Разложение фу-ций по фо-ле Маклорена
- •23.Определение возрастающей(убывающей)фу-ции
- •24.Отыскание точек локального экстремума фу-ции
- •25.Алгоритм нахождения наибольшего и наименьшего значений фу-ций на отрезке
- •26. Первообразной функцией для функции f(X) называется
- •28. Алгоритм интегрирования рацион.Дробей:
- •29. Универсальная тригоном подстановка
- •32.Интегралы типа ,
- •35.Матрицей размера mxn называется
- •36. Определитель(detA)-
- •38.Рангом матрицы называется
- •39.Система линейных алгебраических уравнений—
- •41.Вектором наз.
- •42.Проекция вектора на ось
- •43.Базисом на пл-сти
- •44. Направление в-ра в пространстве
- •46.Векторным произв. *называется
- •55.Исследование общего уравнения плоскости
- •57. Прямая в пр-ве может быть задана
- •60. Цилиндрической пов-тью наз
- •61. Понятие фнп
- •64.Неявно заданная фу-ция
- •65.Линии уровня.Градиент
- •66. Точка m0(x0;y0) называется точной локального максимума(минимума) функции двух переменных
- •67.Понятие об условном экстремуме.
43.Базисом на пл-сти
наз-ся 2 линейно-независимых(не колиниарных)век-ра этой пл-сти взятых в определен.порядке.
Базисом в прост-ве наз. 3 линейно-независимых (не комплонарных) век-ра взятых в определённом порядке.
Теорема:если
век-ры
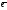 1и
1и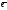 2
образ. базис на плос-ти,то любой ек-ор
2
образ. базис на плос-ти,то любой ек-ор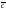 этой плос-ти можно единствен.способом
представить в виде линейной комбинации
базисных век-ов:
этой плос-ти можно единствен.способом
представить в виде линейной комбинации
базисных век-ов: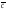 =x
=x
 1+y
1+y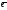 2(такое
представление назыыв.разложением в-ра
2(такое
представление назыыв.разложением в-ра
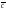 по базису {
по базису {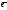 1;
1;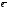 2},такжеx,y-назыв.координатами
в-ра в
2},такжеx,y-назыв.координатами
в-ра в
 базисе {
базисе { 1;
1;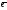 2}.
2}.
Теорема:если
в-ра
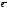 1,
1,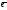 2
,
2
,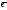 3
образ.базис в простр-ве ,то
3
образ.базис в простр-ве ,то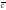 =x
=x
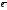 1+y
1+y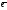 +z
+z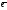 3(x,y,z-координаты
в-ра ра
3(x,y,z-координаты
в-ра ра
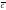 базисе {
базисе {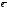 1;
1;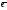 2,
2,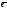 3}.
3}.
44. Направление в-ра в пространстве
опред-тся
углами ![]() ,
кот. вектор образует с осями координат.
Косинусы этих углов наз.направляющими
косинусами вектора:
,
кот. вектор образует с осями координат.
Косинусы этих углов наз.направляющими
косинусами вектора: ![]() ,
,![]() ,
,![]() .
.
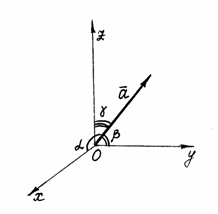
Рис. 12
Из
свойств проекций:![]() ,
,![]() ,
,![]() .
Следовательно,
.
Следовательно,
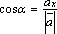 ,
, 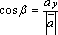 ,
, .
.
Легко показать, что
1) ![]() ;
;
2) координаты
любого единичного вектора совпадают с
его направляющими косинусами: ![]() .
.
Единичный вектор - вектор, абсолютная величина (модуль) кот. равен единице. Единичный вектор, направленный вдоль оси Х, обозн-ся i, единичный вектор, направленный вдоль оси Y , обозн-тся j, а единичный вектор, направленный вдоль оси Z, обозн-тся k. Векторыi, j, k называются , они имеют единичные модули, то есть i = 1, j = 1, k = 1.
45.Скалярным
произведением двух
векторов (![]() или
или![]() )
наз. число, равное произведен. длин этих
ве-ров на косинус угла между ними:
)
наз. число, равное произведен. длин этих
ве-ров на косинус угла между ними:![]() ,
где
,
где![]() .
.
Св-ва скалярного произведения:
1) ;
![]()
2) ![]() ;
;
3) ![]() ;
;
4) ![]() ,
или
,
или![]() ,
или
,
или![]() (в-ры
ортогональны).
(в-ры
ортогональны).
5) a • a = | a |²;
6)![]()
7) i•i=j•j=k•k=1
Приложение скалярного произведения
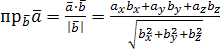
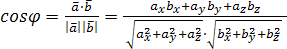
46.Векторным произв. *называется
вектор
с=[![]() ;
;![]() ]=
]=![]() ×
×![]() ,
который удовлетворяет 3 услов.:
,
который удовлетворяет 3 услов.:
1)![]() где
где![]()
2)
![]() ,
,![]()
3)
![]() ,
,![]() ,
,![]() -правая
тройка, т.е кратчайший поворот от правого
вектора
-правая
тройка, т.е кратчайший поворот от правого
вектора![]() к
к![]() виден через с по часовой стрелке.
виден через с по часовой стрелке.
Свойства:
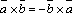 ;
;
2)![]()
3)
![]() ×(
×(![]() +с)=
+с)=
![]() ×
×![]() +
+![]() ×
×
4)
![]()
5) ![]() ,
или
,
или![]() ,
или
,
или![]() ;
;
6)
![]()
![]() ;
;
![]() ;
;![]() ;
;![]()
Геометрическое приложение:
![]() ,
, ![]()
Механическое приложение:
М=ОА×F
47.Смешанным произв. 3-ёх векторов назыв.
скалярное
произв.
![]() ,
,![]() на
на ![]() .
.![]() .
.
Свойства:
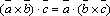
 ×
× *
*  =
= ×
×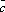 *
* =
= ×
× *
*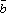 =-
=-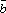 ×
× *
*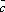 =-
=- ×
× *
*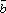 =-
=-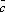 ×
×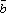 *
*
(λ
 )×
)×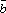 *
*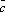 =λ(
=λ( ×
×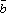 *
*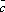 )
)(
 1+
1+ 2)×
2)×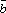 *
*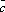 =
= 1×
1×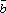 *
*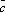 +
+ 2×
2×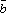 *
*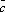
Если
 ,
,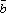 ,
,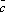 образ. Правую тройку, то их смешанное
произв.>0;
если-левую
<0
образ. Правую тройку, то их смешанное
произв.>0;
если-левую
<0 ×
×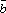 *
*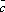 =0
=0
 ,
,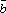 ,
,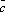 -компланарны
(условие компланарности)
-компланарны
(условие компланарности)
48. Ax+By+C=0-общее уравнение прямой на плоскости
 каноническое
уравнение
каноническое
уравнение
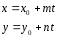 параметрическое
уравнение
параметрическое
уравнение
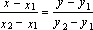 уравнение
прямой, проходящей через
две данные точки.
уравнение
прямой, проходящей через
две данные точки.
![]() ,
,![]() . уравнения
прямой с угловым коэффициентом
. уравнения
прямой с угловым коэффициентом
49. Угол между двумя прямыми
tgϕ=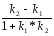 ,
,![]() ,
, ![]() ,где
,где ![]() ,
, ![]()
Условие
перпендикулярности 2-ух прямых: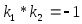
Условие
параллельности: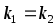
50. Расстояние от точки до прямой на плоскости
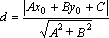
Расстояние
от точки до плоскости

51. Эллипс
Каноническое уравнение
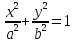 (a>0,
b>0)
(a>0,
b>0)
a-большая полуоси, b-малая полуоси эллипса
(a,0),(-a,0),(0,b),(0,-b)- вершины эллипса;
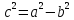
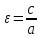 (ε‹1)
– эксцентриситет эллипса
(ε‹1)
– эксцентриситет эллипса
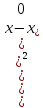 -
уравнение эллипса с осями, параллельными
координатным, и центром симметрии
-
уравнение эллипса с осями, параллельными
координатным, и центром симметрии
 (
(
52. гипербола
Каноническое уравнение
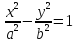
а- действительная, b- мнимая полуоси;
(a,0),(-a,0)-
вершины гиперболы
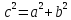
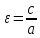 (ε›1)
– эксцентриситет гиперболы
(ε›1)
– эксцентриситет гиперболы
 -
уравнение гиперболы с осями, параллельными
координатным осям
-
уравнение гиперболы с осями, параллельными
координатным осям
53. парабола
Каноническое уравнение
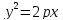
p>0
– расстояние от фокуса до директрисы
– параметр
параболы. Вершина
параболы - точкаO(0,0),
ось Ox-ось
симметрии. Уравнение директрисы ᶩ
параболы: x=
-
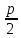
парабола
с вершиной в начале координат , симметрична
относительно оси Оу, имеет уравнение
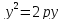
54. Плоскость. Различные виды уравнения плоскости.
*плоскость в пространстве
Ax+By+Cz+D=0,
(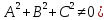 – общие уравнение плоскости
– общие уравнение плоскости
Расположение плоскости в зависимости от значений коэффициентов А,В,С,Д
|
Пл. проходит через начало координат |
D=0, Ax+By+Cz+D=0 |
|
Пл.ǁОх n(вектор) _l_Ох→A=0 |
A=0, By+Cz+D=0 |
|
Пл. проходит через Ох |
A=0, D=0 , By+Cz=0 |
|
Пл. ǁ Оу и Ох |
A=0, B=0, Cz+D=0 |
|
Координатная плоскость Оху |
A=0, B=0, D=0, z=0 |
|
Координатная плоскость Оуz |
X=0 |
|
Координатная пл.Охz |
Y=0 |
Уравнение плоскости в пространстве
|
Три точки M1(x1,y1,z1)ͼQ M2(x2,y2,z2)ͼQ M3(x3,y3,z3)ͼQ |
|
|
Точка М0(х0,у0,z0) и вектор n={A,B,C} _l_Q |
A(x-x0)+B(y-y0)+C(z-z0)=0 |
|
Плоскость Q отсекает отрезкиa, b, c, на осях Ox, Oy и Oz соответственно |
|
Взаимное расположение плоскостей Q1 и Q2 в пространстве
|
Q1ǁQ2 ↔n1ǁn2 |
|
|
Q1 и Q2 совпадают |
|
|
Q1 _l_ Q2 ↔n1 _l_n2 |
A1A2+B1B2+C1C2=0 |
|
Q1 b Q2 пересекаются под углом γ |
Сos
γ= |
|
Расстояние d от точки M0(x0,y0,z0) до плоскостиQ: Ax+By+Cz+D=0 |
d=d(M0,Q)= |