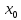1.Опред. ф-ции:

пусть X и Y некот. числовые множества, если кажд. элементу x є X по некоторому правилу f поставлено в соотв. с опред. число y є Y, то говорят, что на множестве X задана ф-ция y=f(x). При этом х назыв. аргументом, у назыв. функцией, X- обл. опред. ф-ции, Y-множ. знач. ф-ций. Способы задания ф-ции: аналитический, графический, табличный. Основные хар-ки повед. ф-ции: 1) y=f(x), четная, если её обл. опред. симметрична относительно нуля и f(-x)=f(x). 2) y=f(x), нечетная, если её обл. опред. симметрична относительно нуля и f(-x)=-f(x). 3) y=f(x), назыв. возраст. yа промежутке X, если большему значению аргумента из этого промежутка соотв. большее знач. ф-ции. 4) y=f(x), назыв. убывающей на промежутке X, если большему значению аргумента из этого промежутка соотв. меньшее значение ф-ции. 5) ф-ция назыв. ограниченной сверху (снизу) на промежутке X, если сущ. такое число M(m), что для всех x из этого промежутка f(x)≤M (f(x)≥m). 6) ф-ция y=f(x) назыв. ограниченной на промежутке X, если сущ. такое число M > 0, что для всех х из этого пром. │f(x)│≤ M. Если ф-ция ограничена на пром., то она огран. на этом пром. и сверху и снизу. 7) ф-ция f(x) назыв. переодичной с периодом (T≠0), если для всех значений х из обл. опред. ф-ции справедливо равенство f(x+T)=f(x). Основные элементарные ф-ции: степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические. Элементарной ф-цией называется ф-ция построенная из основных элементов ф-ции и постоянных с помощью конечного числа операций, сложения, вычитания, умножения, деления и взятия композиции ф-ции. Алгебраическая классиф. эл. ф-ций: 1) рациональные ( а)дробные, б)целые ), 2) иррациональные ф-ции

2.Определение предела ф-ции на языке окрестностей:

Число называется пределом функциипри, если для любого положительного числанайдётся положительное числотакое, что значения функциипринадлежат-окрестности точкидля всехиз выколотой-окрестности точки если для такое, чтодляПредел ф-ции на языке последовательностей: Предел функции равенпритогда и только тогда, когда для любой последовательности,cходящейся к и, соответствующая последовательность значений функциисходится к. ( для ). Односторонние пределы: Число A назыв. пред. ф-ции f(x) х→х₀ справа (слева), если для любого ε окр. А найдется такая правостор. (левосторон.), что для всех х из этой окрестности точки х₀ соотв. значение f(x) попадут в указанную ε окр. точки А.

3.Теорема о локальной ограниченности функции, имеющей при конечный предел

: ,

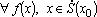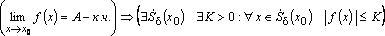т.е. если функция при  имеет конечный предел, то существует окрестность точки , на которой множество значений функции  есть ограниченное числовое множество.

4.Функция называется бесконечно малой

при , если

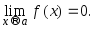
Свойства: 1) (о связи функции с ее конечным пределом). (конечное) тогда и только тогда, когда, гдебесконечно малая функция при . 2) (о произведении бесконечно малой функции на ограниченную).Пусть функция − бесконечно малая при , а функция − ограничена в некоторой выколотой окрестности точки . Тогда произведение этихфункций является бесконечно малой функцией при 3)(о сумме, разности, произведении бесконечно малых). Сумма, разность, произведение конечного числа бесконечно малых функций при есть функция бесконечно малая при . (об эквивалентных бесконечно малых). Пусть при. Тогда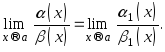

5.Функция называется бесконечно большой

при , если .

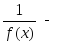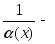Свойства ББФ: 1) (о связи с бесконечно малой). Если функция бесконечно большая при, то функция бесконечно малая при .Если функция бесконечно малая приив выколотой окрестности точки, то функция бесконечно большая при . 2) (об арифметических операциях).1). Произведение двух бесконечно больших при есть бесконечно большая при .2). Произведение бесконечно большой при на функцию, имеющую ненулевой предел при ,есть бесконечно большая при.3). Отношение бесконечно большой при к бесконечно малой (отличной от нуля) при есть бесконечно большая при .4). Сумма двух бесконечно больших одного знака при есть бесконечно большая того же знака при .

6. Всего существует 7 видов неопределённостей.

[0/0] [] [[] [ []

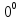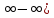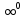Первый замечательный предел

Второй замечательный предел

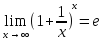
7. Определение непрерывности функции в точке.

Определение 1. Функция y=f(x) называется непрерывной в 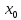точке , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке.

Определение2. Функция y=f(x) называется непрерывной в 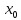точке , если предел функции в этой точке равен значению функции в этой точке.

Три условия непрерывности: 1. f(x) определена в точке и некоторой её окрестности.2.Существуют конечные односторонние пределыf(x) в точке 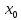3.f(=f(=0

Классификация точек разрыва.

1.Первого рода( если выполняется 1 и 2 условия, но не выполняется 3)

-Точки устранимого разрыва(односторонние пределы равны, но не равны значению функции в этой точке)

-Точки устранимого разрыва( существуют конечные односторонние пределы, но они не равны между собой)

2.Второго рода(если хотя бы один из пределов не существует или равен бесконечности)

-Точки бесконечного разрыва(если односторонние пределы существуют но хотя бы один из них равен бесконечности)

-Точки несуществования( хотя бы один из односторонних пределов не существует)

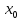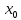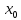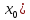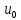Основные свойства функций непрерывных в точке. Теорема 1. Основные элементарные функции непрерывны во всех точках внутри своей области определения. Теорема 2. Если функция f(x) и g(x) непрерывны в точке , то функцияf(x)+-g(x) нерперывны и f(x)/g(x) непрерывна в точке , еслиg(x) в точке не равно 0.Теорема 3. Если f(u) непрерывна в точке ,u(x) непрерывна в точке б причемu(=, тоf(u(x)) нерперывна в точке