
- •2.Определение предела ф-ции на языке окрестностей:
- •3.Теорема о локальной ограниченности функции, имеющей при конечный предел
- •4.Функция называется бесконечно малой
- •5.Функция называется бесконечно большой
- •8.Понятие непрерывности функции на промежутке.
- •9.Асимптотой графика функции называется
- •12. Произв сложн ф-и
- •13. Производная обратной функции равна
- •16.Теорема Ферма.Геометрический смысл теоремы Ферма.
- •17.Теорема Ролля.Геометрический смысл теоремы Роля.
- •18.Теоремы Лагранжа и Коши.Геометрический смысл теоремы Лагранжа.
- •19.Правило Лопиталя
- •20.Сравнение роста показательной,степенной и логарифмической функций.
- •22.Разложение фу-ций по фо-ле Маклорена
- •23.Определение возрастающей(убывающей)фу-ции
- •24.Отыскание точек локального экстремума фу-ции
- •25.Алгоритм нахождения наибольшего и наименьшего значений фу-ций на отрезке
- •26. Первообразной функцией для функции f(X) называется
- •28. Алгоритм интегрирования рацион.Дробей:
- •29. Универсальная тригоном подстановка
- •32.Интегралы типа ,
- •35.Матрицей размера mxn называется
- •36. Определитель(detA)-
- •38.Рангом матрицы называется
- •39.Система линейных алгебраических уравнений—
- •41.Вектором наз.
- •42.Проекция вектора на ось
- •43.Базисом на пл-сти
- •44. Направление в-ра в пространстве
- •46.Векторным произв. *называется
- •55.Исследование общего уравнения плоскости
- •57. Прямая в пр-ве может быть задана
- •60. Цилиндрической пов-тью наз
- •61. Понятие фнп
- •64.Неявно заданная фу-ция
- •65.Линии уровня.Градиент
- •66. Точка m0(x0;y0) называется точной локального максимума(минимума) функции двух переменных
- •67.Понятие об условном экстремуме.
16.Теорема Ферма.Геометрический смысл теоремы Ферма.
Теорема Ферма. Пусть функция y = f(x) определена в интервале (а, в) и принимает в точке этого интервала наибольшее или наименьшее на (а, в) значение. Тогда если f(x) дифференцируем в точке х(нулевое),то f’(x)=0
Доказательство.
Пусть, например, f(с) = М –
наибольшее значение функции в интервале
(а,
в)
и существует f'(с). По
определению производнойf'(с)=![]() .
При любом знаке х
f(c+x)-f(c)≤0,
так как f(с)
– наибольшее значение функции в (а,
в).
.
При любом знаке х
f(c+x)-f(c)≤0,
так как f(с)
– наибольшее значение функции в (а,
в).
Если х>0,
то ![]() и,
следовательно, f'(с)≤0. Если
же х<0, то
и,
следовательно, f'(с)≤0. Если
же х<0, то ![]() и f'(с) ≥0.
Следовательно, f'(с)=0.
и f'(с) ≥0.
Следовательно, f'(с)=0.
Геометрический смысл. теорема означает, что касательная, проведенная к графику функции в точке (с; f(с)), параллельна оси Ох.
17.Теорема Ролля.Геометрический смысл теоремы Роля.
Теорема Роля.Пусть функция f(x) удовлетворяет 3 условиям:1) непрерывна на отрезке [a, b]
2) дифференцируема на интервале (a, b)
3)на концах отрезка принимает одинаковые значения,т.е. f(a) = f(b) = 0.
Тогда ее производная f'(х) обращается в нуль хотя бы в одной точке с( a, b).
Доказательство. По условию функция y = f(x) непрерывна на отрезке [a, b], поэтому она достигает на [a, b] своего наибольшего М и наименьшего m значений. Если М = m, то функция постоянна на [a, b] и ее производная f'(х) = 0 во всех точках (a, b). Пусть теперь М m, тогда хотя бы одно из этих чисел, например, m 0. Поэтому существует точка с( a, b) такая, что f(с) = m. Следовательно, по теореме Ферма f'(с) = 0.Т.Ролля опирается на т.Ферма и т.Вейерштрасса.
Геометрический смысл. теорема означает, что если функция y = f(x) удовлетворяет теореме Ролля, то найдется хотя бы одна точка (с; f(с)), где с(a;b),такая, что касательная к графику функции, проведенная в этой точке, параллельна оси Ох.
18.Теоремы Лагранжа и Коши.Геометрический смысл теоремы Лагранжа.
Теорема
Лагранжа.
Пусть
функция f(x):1.непрерывна
на отрезке [a, b];
2.дифференцируема в интервале (a, b).Тогда
существует 1 точка с (a, b)
внутри интервала,в которой
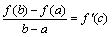
Доказательство.т.Лагранжа
опирается на т.Ролля,которую нужно
применить к функции
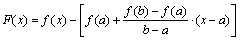
Геометрический смысл т.Лагранжа. Теорема Лагранжа означает, что существует хотя бы одна точка с (а, b) такая, что касательная, проведенная к графику функции в точке (с; f (с)), параллельна хорде АВ.
Теорема
Коши.
Если функции f (х)
и ![]() (х)
непрерывны на отрезке [а, b]
и дифференцируемы в интервале (а, b),
причем
(х)
непрерывны на отрезке [а, b]
и дифференцируемы в интервале (а, b),
причем ![]() ,
то существует точка с (а,b)
такая, что
,
то существует точка с (а,b)
такая, что
![]()
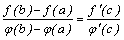
Доказательство. Рассмотрим функцию
F(х) = [f(х)-f(а)] – 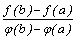 .
[
.
[![]() (х)-
(х)-![]() (а)].
(а)].
Легко
проверить, что эта функция удовлетворяет
теореме Ролля (аналогично тому, как это
было сделано в предыдущей теореме).
Следовательно, существует точка с (a,
b.)
такая, что ![]()
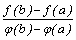 .
. 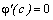
19.Правило Лопиталя
Правило
Лопиталя.Предел
двух бесконечно малых и двух бесконечно
больших функций равен пределу отношения
их производных,если последний предел
существует.
Пусть ![]() -
функции, непрерывные на [а, b],
дифференцируемые в(а, b);
-
функции, непрерывные на [а, b],
дифференцируемые в(а, b); ![]() при
всех х (а, b)
и f (а)
=
при
всех х (а, b)
и f (а)
= ![]() (а) = 0.
(а) = 0.
Тогда,
если существует 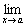
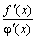 ,
то существует
,
то существует 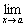
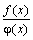 ,причем
,причем 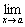
 =
= 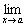
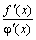 .
.
Правило Лопиталя формулируется для раскрытия неопределённости [бесконечность,бесконечность],[ноль,бесконечность].
Доказательство.
Возьмем
на [а, b]
какую-нибудь точку х ![]() а.
Применяя формулу Коши, получим
а.
Применяя формулу Коши, получим  ,
где с (а;
х).
,
где с (а;
х).
По
условию f (а) = ![]() (а) = 0, значит
(а) = 0, значит  .
Если х
.
Если х ![]() а, то
и с
а, то
и с![]() а, так
как с (а, х).
а, так
как с (а, х).
При
этом, если существует 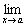
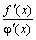 =А,
то существует и
=А,
то существует и 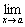
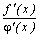 =
А.
=
А.
Поэтому ![]()
 =
= 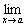
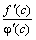 =
= 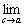
 =
= ![]()
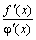 =
А.
=
А.
