8.Понятие непрерывности функции на промежутке.

Функция f(x) непрерывна на отрезке [a;b], если она непрерывна в каждой точке интервала (a;b), в точке а она должна быть неперывна справа, а в точке в она непрерывнва слева.

Свойства функций непрерывных на отрезке.

Теорема Вейерштрасса. Если функция f(x) определена и непрерывна на отрезке [a;b], то она ограничена на этом отрезке и достигает на нём своих наибольшего и наименьшего значения.

Теорема Бальцано-Каши. Если f(x) непрерывна на отрезке [a;b] и на концах отрезка принимает значения разных знаков, то существует тоска с(а;в) на которой функция обращается в 0

Теорема Бальцано-Каши. Если f(x) непрерывна на отрезке [a;b] и обозначим f(a)=A, f(b)=B, то для любого числа С между А и В найдётся такое чисто С внутри отрезка что f(c)=C

9.Асимптотой графика функции называется

прямая, обладающая тем свойством, что расстояние от точек до этой прямой стремится к 0, при бесконечном удалении точек графика от начала координат.

Прямая x= является вертикальной асимптотой графика функции, если функция определена в некоторой(возможно проколотой) окрестности точки 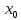и хотя бы один из односторонних пределов функции в этой точке равен бесконечности

Если существует конечный предел при x стремящимся к бесконечности , то прямая y=b являестя правосторонней горизонтальной асимптотой графика функции

Если существуют конечные пределы 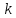и в, то прямаяy=kx+в является правосторонней асимптотой графика функции

10. Производная и её связь с дифференциалом.

Функция дифференцируема в точке 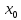тогда и только тогда, когда в этой точке существует конечная производная этой функции.

Геометрический смысл производной функции f(x) в точке 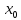это тангенс угла наклона касательной к графику функции в точке с координатами (

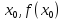
Механический смысл производной. Производная выражает мгновенную скорость изменения функции в момент времени

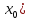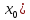Уравнение касательной y=f((x-+f(

Основные правила дифференцирования:

C’=0

(u+-v)’=u’+v’

(uv)’=u’v+uv’

(cu)’=cu’

(u/v)’=u’v-uv’/v^2

11.ф-я y=f(x) наз диференц-ой в т x0,

если ее превр в этой точке можно представ в виде ∆y=A*∆x+0(∆x), 0(∆x)-бесконмалое,А-завис от ф-и от т x0,но не завис от ∆x.Ф-я наздиф-ой на промеж,если она диф-ма в кажд т этого промеж.

Связь диф-ти и производной:ф-ядиф-ма в т x0тогда,когда в этой т существ конечнпроизводн этой ф-и.Док-во1:пусть ф-я я y=f(x)диф в т x0 из этого след что ее превращен в этой т можно представ в виде ∆y=A∆x+0(∆x).f(x0)=limy/x=A+lim 0(∆x)/∆x=A.Док-во2:сущконечнпроизв ф-и в т равносильндиф-ти ф-и в т и этого след операция нахожденпроизвназывдиф-ем.dy=y(x0)dx

Связь диф-ти и непрерывности:если ф-я диф-ма в т x0,то она непрер.Док-во:пусть ф-я y=f(x) в т x0 из этого след виде ∆y=A∆x+0(∆x).lim∆y=0.

12. Произв сложн ф-и

=произведен произодн этой ф-и по промеж аргуенту на производн промеж аргум по осн аргументу.

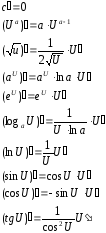
13. Производная обратной функции равна

обратной величине производной данной функции.

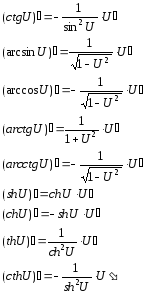
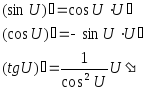
14.диф-е неявно задан ф-й:

пусть ф-я у завис от х задается не явным ур-ем f(x,y)=0.чтобы найти произв этой ф-и по перемен х нужно продиференц по х обе части равенства,помня у-ф-я от х.

диф-е параметрически задан ф-й:ф-я у(t) и x(t)ди-мы отtна некотпромеж,ф-я у(t) и x(t) имеют на этом промеж обратн ф-ю,тогда у=у(t(x)).

15.диф-л 1-го порядка

выражается формул dy=y’xdx не завис от того явл ли х независ перемен или ф-ей друг перемен.св-во наз инвариантностью формы диф 1 пор.между 2 формулами dy=y’xdx и dy=y’udy .диф-л 2-го порядка и выше не облад этим св-ом.

Диф висш порядка:дифференциал явл ф-ей,его можно расматр как ф-ю 2 перемен х и dx,эти перемен не зависемы друг от друга.Диф-ом 2-го порядка наз диф-л от диф-ла 1-го порядка.