Модели в виде уравнений регрессии
|
№ п/п |
Математическая модель |
|
1 |
y = 48,94 + 9,29x1 – 3,26x2 + 8,41x3 – 0,76x1x2 – 2,44x1x3 – 8,24x2x3 |
|
2 |
y = 21,93 + 4,56x1 + 7,76x3 – 0,69x1x2 – 0,44x2x3 |
|
3 |
y = 23,63 + 4,65x1 – 2,15x2 + 5,68x3 – 1,03x1x2 – 5,6x2x3 |
|
4 |
y = 75,78 + 5,13x1 + 7,15x3 – 0,65x1x3 – 3,58x2x3 |
|
5 |
y = 21,77 + 2,97x1 + 4,23x3 – 0,51x1x2 – 2,1x2x3 |
|
6 |
y = 3,59 + 0,69x1 – 1,36x2 + 0,66x3 + 0,26x1x3 |
|
7 |
y = 40,28 + 8,98x1 – 3,27x2 + 10,95x3 – 0,68x1x2 – 1,71x1x3 – 8,65x2x3 |
|
8 |
y = 2100 – 665,4x1 – 242,9x1x2 + 115,4x1x3 – 67,1x2x3 |
|
9 |
y = 26,36 + 0,89x1 – 2,01x2 + 1,89x3 – 1,19x1x2 + 1,01x2x3 |
|
10 |
y = 48,43 + 8,98x1 – 3,3x2 + 8,7x3 – 1,35x1x2 – 1,85x1x3 – 8,13x2x3 |
|
11 |
y = 22,73 + 4,65x1 – 1,28x2 + 10,08x3 – 0,95x1x2 + 0,55x1x3 – 1,48x2x3 |
|
12 |
y = 34,67 + 6,18x1 + x2 + 10,45x3 + 1,95x1x2 – 2,5x1x3 – 5,28x2x3 |
|
13 |
y = 23,8 + 4,68x1 – 2,13x2 + 5,68x3 – 0,95x1x2 – 0,45x1x3 – 5,6x2x3 |
|
14 |
y = 18,14 + 3,69x1 – 1,09x2 + 5,44x3 – 0,14x1x2 – 1,16x1x3 – 3,89x2x3 |
|
15 |
y = 16,79 + 0,61x1 – 3,2x2 + 0,41x3 – 0,6x1x2 – 0,2x1x3 – 0,24x2x3 |
23. Решение дифференциальных уравнений
23.1. Решение уравнений первого порядка
Рассмотрим дифференциальное уравнение первого порядка:
Требуется найти решение на интервале [x0, xn], удовлетворяющее начальному условию y(x0) = y0.
Для приближённого решения дифференциального уравнения интервал [x0, xn] разбивается на n частей с шагом h:
xi+1 = xi + h, i = 0, 1, 2, …, n – 1.
В полученных точках вычисляются значения yi.
Метод Эйлера. Согласно методу Эйлера, значения yi определяются по формуле:
yi+1 = yi + h f(xi, yi).
Алгоритм метода Эйлера:
1. Ввод n, конечного значения xn, начального значения x0 (в переменную x), ввод y0 (в переменную y).
2.
Вычисление h
=
,
x
= x0,
y
= y0.
3. Вывод x, y.
4. Вычисление y = y + h f(x, y), x = x + h.
5. Если x > xn, то переход к п. 6, иначе – переход к п. 3.
6. Конец вычислений.
Для получения достоверных результатов значение h должно быть достаточно мало, при этом можно не выводить все получающиеся значения x и y. Целесообразно внести изменения в алгоритм программы так, чтобы вычисления проводились с малым шагом, а вывод результатов − с большим.
Метод Рунге-Кутта. Расчетные формулы метода Рунге-Кутта четвертого порядка имеют вид:
k1 = h f(xi, yi),
k2
=
h
f(xi
+
,
yi
+
),
k3
=
h
f(xi
+
,
yi
+
),
k4 = h f(xi + h, yi + k3),
yi+1
= yi
+
(k1
+ 2
k2
+ 2
k3
+ k4),
xi+1 = xi + h, i = 0, 1, 2, …, n – 1.
Для разработки программы, реализующей метод Рунге-Кутта можно использовать тот же алгоритм, что и для метода Эйлера, внеся в него соответствующие изменения.
23.2. Системы дифференциальных уравнений и уравнения высших порядков
Система дифференциальных уравнений m-го порядка имеет вид:
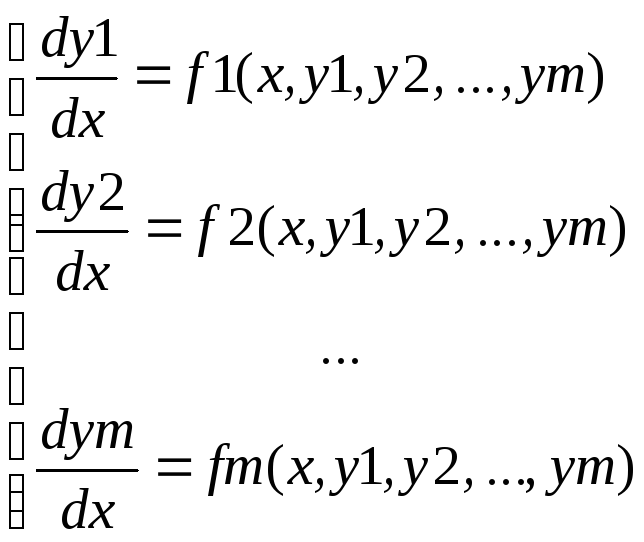
Для решения системы на отрезке [x0, xn] должны быть заданы начальные условия: y1(x0) = y10, y2(x0) = y20 , …, ym(x0) = ym0. Решением системы m-го порядка будут m функций, удовлетворяющих начальным условиям. Чтобы определить эти функции можно использовать метод Эйлера или Рунге-Кутта (или любой другой метод), применяя их к каждому уравнению последовательно.
Уравнения высших порядков сводятся к системам дифференциальных уравнений путем введения новых переменных.
Пример. Требуется решить уравнение y +2 y – y + 4 x = 5 на отрезке [1; 1.3]. Начальные условия: y(1) = 2, y(1) = 0. Шаг h = 0.1. Здесь шаг выбран большим, чтобы было проще продемонстрировать вычисления, сделанные вручную.
Введем новую переменную z = y. Тогда исходное уравнение записывается в виде системы двух уравнений первого порядка:
y = z,
z = –2 z + y – 4 x + 5.
Начальные условия: y(1) = 1, z(1) = 0. Решим данную систему методом Эйлера:
y(1.1) = 2 + 0.10 = 2,
z(1.1) = 0 + 0.1 (–2 0 + 2 – 4 1 + 5) = 0.3,
x = 1 + 0.1 = 1.1,
y(1.2) = 2 + 0.1 0.3 = 2.03,
z(1.2) = 0.3 + 0.1 (–2 0.3 + 2 – 4 1.1 + 5) = 0.5,
x = 1.1 + 0.1 = 1.2,
y(1.3) = 2.03 + 0.1 0.5 = 2.08,
z(1.3) = 0.5 + 0.1 (–2 0.5 + 2.03 – 4 1.2 + 5) = 0.623,
x = 1.2 + 0.1 = 1.3.
Решение: x = 1, y = 2, z = 0.
x = 1.1, y = 2, z = 0.3.
x = 1.2, y = 2.03, z = 0.5.
x = 1.3, y = 2.08, z = 0.623.