20.4. Задание для выполнения на компьютере

1. Составить программу решения системы линейных уравнений по методу Гаусса. Коэффициенты системы даны в таблице.

2. Решить эту же систему с помощью приложений Mathcad и Excel. Результаты сравнить между собой.

3. Решить систему нелинейных уравнений, приведенную выше, в приложении Mathcad.

Таблица

Исходные данные для расчета

№ п/п	а11	а12	а13	а21	а22	а23	а31	а32	а33	b1	b2	b3
1	6	– 3	1	4	8	– 2	7	– 1	9	1.2	1.3	1.4
2	5	– 2	1	1	– 4	– 1	2	– 1	4	1.7	1.6	1.9
3	4	1	– 1	1	– 5	1	2	– 3	6	6.2	2.4	1.8
4	8	2	– 1	1	10	5	2	– 1	– 4	2.3	1.4	1.7
5	5	0.3	0.1	0.2	2	0.8	0.4	0.4	2	7.2	8.3	6.6
6	3	0.6	– 1	0.8	3	1.2	1	0.8	2.6	0.2	– 3	2.7
7	1	0.1	0.1	0.2	1	0.3	0.3	0.4	1	1.5	1.6	1.7
8	4	1.2	1	1.5	2.8	0.7	1	1.5	3.5	7.1	7.7	4.2
9	2.1	– 2	0.3	0.7	1.9	0.6	0.3	0.7	1.5	1.6	0.9	3.5
10	3.1	– 2	0.5	0.8	2.7	– 1	0.5	– 1	2.1	1.3	4	2.3
11	0.1	0.3	0.4	0.2	0.1	0.6	0.4	0.2	0.3	0.7	0.5	0.6
12	4	– 1	2	1	– 5	3	2	1	– 8	1.8	2.5	0.3
13	7.1	– 2	0.7	0.7	3.5	8.4	5.5	5.6	1.3	7.7	0.1	4.5
14	2.5	0.2	0.1	0.1	1	0.4	0.2	0.2	1	3.6	4.2	3.3
15	1.6	0.7	0.2	0.1	– 2	0.5	1	0.2	2.5	1.9	2.6	2.3

21. Математические модели и оптимизация процессов

21.1. Модель одномерного объекта

Пусть в результате проведения эксперимента получена табличная зависимость значений выходного параметра процесса y от значений входного параметра x (рис. 21.1).

Объект

xy

Рис. 21.1. Одномерный объект

Требуется получить эмпирическую формулу, описывающую зависимость y от x. Решение такой задачи состоит из двух этапов.

На первом этапе выбирается общий вид формулы, исходя из теоретических представлений о характере изучаемого процесса. Это может быть, например, полином m-степени:

y = a0 + a1  x + a2  x² +…+ am  x^m.

Формула может содержать тригонометрические, экспоненциальные, логарифмические функции и т. п.

На втором этапе определяются значения параметров a0, a1, …, am эмпирической формулы f(x, a0, a1, a2, …, am), которые обеспечивали бы соответствие этой формулы экспериментальным данным.

В соответствии с методом наименьших квадратов параметры a0, a1, …, am выбираются так, чтобы была минимальной сумма квадратов:

Чтобы найти нужные параметры, следует взять частные производные от правой части по a0, a1, …, am и приравнять их к нулю. Полученную систему уравнений можно решить одним из известных методов.

Пример. Пусть требуется определить параметры a0, a1, a2 полинома второй степени:

y = a0 + a1x + a2x².

Надо взять частные производные от выражения

и приравнять их к нулю:

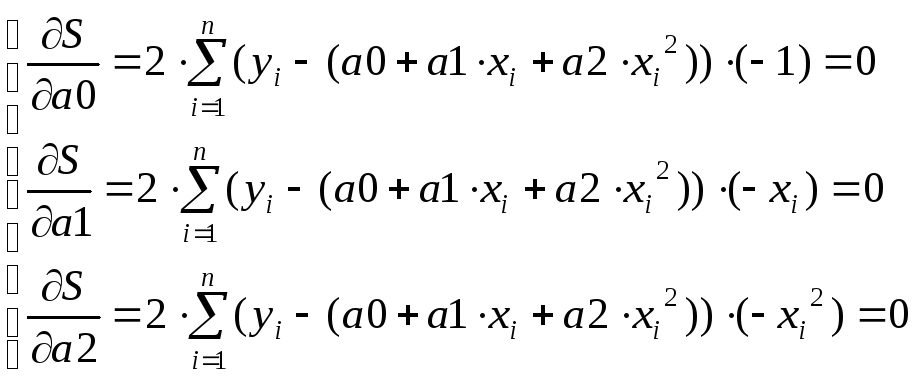
Отсюда

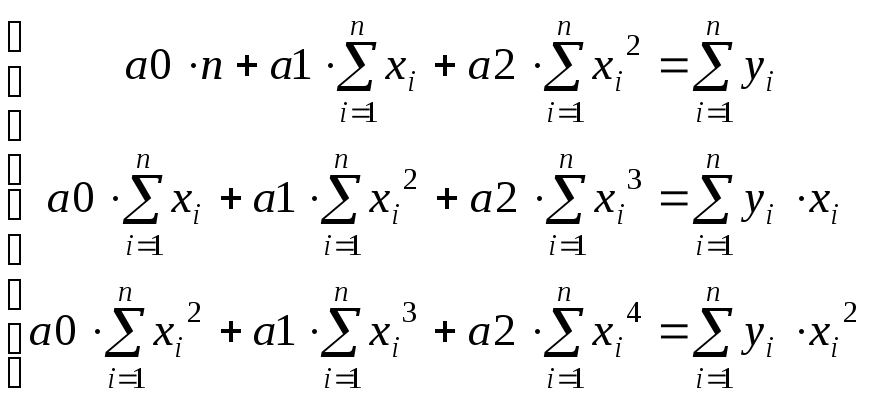
Решив эту систему линейных урвнений можно определить искомые величины a0, a1, a2.

Рассмотрим алгоритм метода наименьших квадратов для вычисления коэффициентов полинома второй степени:

1. Ввод количества опытов n, значений x₁, x₂, …, x_n, y₁, y₂, …, y_n.

2. Определение коэффициентов системы линейных уравнений:

a_1,2 = a_1,3 = a_2,3 = a_3,3 =

b₁ = , b₂ = b₃ =

a_1,1 = n, a_2,1 = a_1,2, a_2,2 = a_1,3, a_3,1 = a_1,3, a_3,2 = a_2,3.

3. Решение системы A  Z = B, где A – матрица коэффициентов, B – вектор свободных членов системы, Z – вектор, в котором определяются корни z₁ = a0, z₂ = a1, z₃ = a2.

4. Вывод искомых коэффициентов a0, a1, a2.

5. Определение и вывод разностей ₁, ₂, …, _n.