Лекция 4. Механические колебания. Акустика

Колебаниями называют любые процессы, более или менее точно повторяющиеся через равные промежутки времени.

В зависимости от физической природы процесса различают колебания механические, температурные, электромагнитные и т.д. Однако все колебания подчиняются общим закономерностям, которые описываются аналогичными математическими уравнениями. Рассмотрим эти закономерности на примерах свободных (без приложения внешних сил) и вынужденных (с приложением внешних сил) механических колебаний.

4.1. Гармонические колебания и их характеристики

Гармоническими колебаниями называют периодическое изменение какойлибо физической величины (в механике – перемещения или угла поворота) вблизи ее равновесного значения. Эти колебания описываются функциями синус или косинус.

Рассмотрим характеристики колебаний на примере свободных колебаний маятника при отсутствии сил сопротивления (трения).

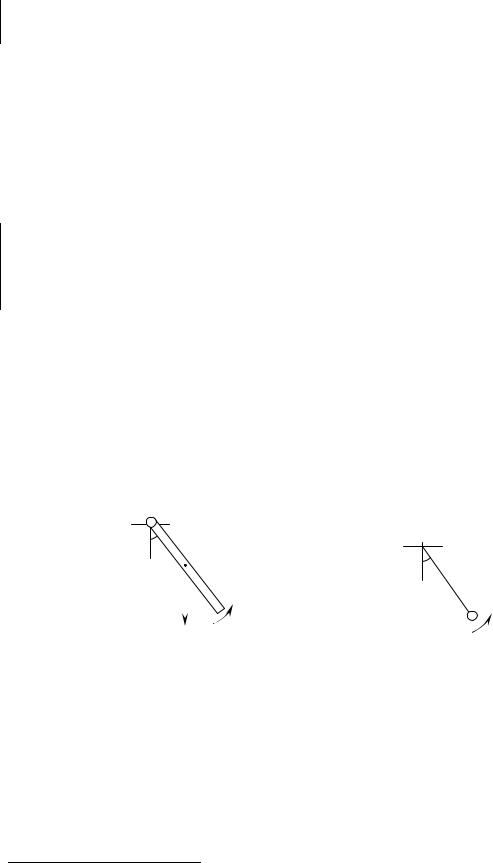
Физическим маятником называют твердое тело, которое совершает колебания вокруг неподвижной горизонтальной оси. На рис. 4.1 изображен качающийся стержень.

Математическим маятником называют материальную точку, которая совершает колебания вокруг неподвижной горизонтальной оси. Это частный случай физического маятника. На рис. 4.2 изображен небольшой шарик на легкой нерастяжимой (жесткой) нити.

Пусть тело массы m закреплено в точке О и совершает малые1 свободные колебания вокруг оси, проходящей через эту точку и перпендикулярной плос-

кости рисунка (рис. 4.1). Сопротивлением воздуха пренебрегаем.

Из основного уравнения динамики вращательного движения (3.6)

Jε = M.

Момент создается только одной силой – силой тяжести, причем сила действует против направления вращения, и знак момента будет отрицательным

M = –Mmg = –mglsinϕ ≈ –mglϕ,

1 Для малых колебаний характерны относительно небольшие отклонения величин от равновесного значения. В данном случае угол отклонения маятника маленький ϕ → 0 (в радианах). А в градусах угол не превышает 10°.

26

где l − расстояние от оси вращения О до центра масс тела С. Из определений углового ускорения и угловой скорости

ε = ω′(t), ω = ϕ′(t),

получим

ε = ϕ″(t).

Тогда с учетом преобразований основное уравнение будет иметь вид

Полученная функция ϕ(t) описывает гармонические колебания и определяет угол отклонения маятника от положения равновесия в момент времени t. Свободные колебания без сил сопротивления являются гармоническими.

Прежде чем перейти к характеристикам гармонических колебаний, отметим, что уравнения (4.1) и (4.2) носят общий характер. Уравнения такого вида описывают любые гармонические колебания, а не только колебания маятника. В зависимости от природы колеблющейся величины вместо угла поворота может быть перемещение, температура, сила тока, напряжение и т.д. Вид уравнений будет аналогичный.

Характеристики колебаний.

А – амплитуда – максимальное отклонение колеблющейся величины от положения равновесия.

ω0 − циклическаячастота(формулазависитотвидаколебаний, размерностьрад/с). ω0t + δ − фаза (размерность рад).

δ− начальная фаза.

ν= ω0/(2π) – частота (размерность с–1 = Гц).

Т = 1/ν = 2π/ω0 – период – время одного колебания.

Период колебаний физического маятника определяется формулой

где m − масса тела, J − момент инерции тела относительно оси вращения (оси колебаний), l − расстояние от оси вращения до центра масс тела.

Если взять небольшой по размерам шарик на легкой нити длины l, у нас получится математический маятник (шарик можно считать материальной точкой, если его радиус много меньше длины нити). Момент инерции шарика от-

носительно оси колебаний J = ml2. Тогда период колебаний математического маятника

Эта формула хорошо известна из школы.

Графически вид гармонических колебаний изображен на рис. 4.3. Это общий вид графика функции (4.2).

Если колебания совершаются вдоль одной оси, например, груз на пружине, то методом аналогии можно сразу получить формулу для энергии таких колебаний

Итак, полная энергия гармонических колебаний не зависит от времени и

пропорциональна квадрату амплитуды.

4.2. Затухающие колебания

Однако в природе и технике любые свободные колебания не могут совершаться бесконечно долго, поскольку всегда действуют силы сопротивления. Без притока энергии извне (без внешних воздействий) любое колебание рано или поздно прекращается. И механическая или электромагнитная энергия колебаний превращается в тепловую (внутреннюю) энергию.

Колебания, амплитуда которых уменьшается со временем под действием сил сопротивления, называются затухающими.

Обычно силы сопротивления среды при небольших скоростях движения пропорциональны скорости (при больших – квадрату скорости). Соответственно момент силы сопротивления пропорционален угловой скорости

MFc = αω = αϕ′.

28

где γ = α/(2J) – коэффициент затухания.

Это дифференциальное уравнение затухающих колебаний. Его решение

затухающих колебаний, δ – начальная фаза колебаний.

Функция (4.6) описывает затухающие колебания. Вид этой функции показан на рис. 4.5. Затухающие колебания негармонические.

t

−A

Рис. 4.5

Отметим, что, чем больше коэффициент затухания γ, тем быстрее уменьшается амплитуда колебаний. Когда γ становится больше ω0, колебаний вообще не будет, амплитуда монотонно стремится к нулю.

4.3. Вынужденные колебания

Чтобы система совершала незатухающие колебания, необходимо восполнять извне потери энергии. Для механической системы это означает, что надо приложить внешнюю периодическую силу

F(t) = F0 cosωt,

где F0 и ω – амплитуда и циклическая частота этой силы.

Если тело совершает колебания под действием периодической силы F(t),

29