diplom25 / suslov_ibragimov_ekonometrika

ei2

s22

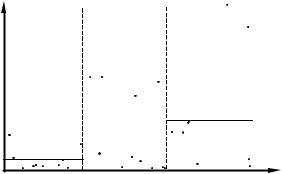
Рис. 8.3

в которой,правда,угловой коэффициент и свободный член меняются местами.Тем

самым применяется преобразование в пространстве наблюдений такое,что диаго-

"

нальные элементы матрицы D равны 1 zi .

Если зависимость дисперсии от других переменных известна не точно,а только с точностью до некоторых неизвестных параметров,то для проверки гомоскедастичности следует использовать вспомогательные регрессии.

Так называемый метод Глейзера состоит в следующем.Строится регрессия модулей остатков |ei| на константу и те переменные,которые могут быть коррелированными с дисперсией(например,это может быть все множество независимых факторов или какое-то их подмножество).Если регрессия оказывается статистически значимой,то гипотеза гомоскедастичности отвергается.

Построение вспомогательной регрессии от некоторой переменной yi показано на рисунке8.3.

Другой метод( критерий Годфрея)использует аналогичную вспомогательную регрессию,в которой в качестве зависимой переменной используются квадраты остатков e2i .

Если с помощью какого-либо из перечисленных критериев(или других аналогичных критериев)проверены различн ые варианты возможной зависимости и нулевая гипотеза во всех случаях не была отвергнута,то делается вывод,что ситуация гомоскедастична или гетероскедастична без негативных последствий и что для оценки параметров модели можно использовать обычный МНК.Если же нулевая гипотеза отвергнута и поэтому,возможно,имеет место гетероскедастичность с негативными последствиями,то желательно получить более точные оценки,учитывающие гетероскедастичность.

Это можно сделать,используя для оц енивания обобщенный МНК(см.уравнение(8.2)).Соответствующее преобразование в пространстве наблюдений состоит

в том,чтобы каждое наблюдение умножить на di ,т.е.требуется оценить обычным методом наименьших квадратов преобразованную регрессию с переменными diXi и di Zi .При этом не следует забывать,что если матрица факторов Z содержит свободный член,то его тоже нужно умножить на di ,поэтому вместо свободного члена в регрессии появится переменная вида (d1, . . . , dN ).Это приводит к тому, что стандартные статистические пакеты выдают неверные значения коэффициента детерминации и F -статистики.Чтобы этого не про исходило,требуется пользоваться специализированными процедурами для расчета взвешенной регрессии. Описанный методполучил названиевзвешенного МНК,посколькуонравнозначен

минимизации взвешенной суммы квадратов остатков %N d2i e2i .

i=1

Чтобы это можно было осуществить,необ ходимо каким-то образом получить оценкуматрицы D,используемойдляпреобразованиявпространственаблюдений. Перечисленные в этом параграфе методы дают возможность не только проверить гипотезу об отсутствии гетероскедастичности,но и получить определенные оценки матрицы D (возможно,не очень хорошие).

Если S2 Ñоценка матрицы σ2Ω ,где S2 Ñдиагональная матрица,составленная из оценок дисперсий,то S−1 (матрица,обратная к ее квадратному корню) Ñоценка матрицы σD.

Так,после проверки гомоскедастичности методом Глейзера в качестве диа-

то наблюдения разбиваются на группы,для каждой из которых есть оценка дис-

персии, s2.Тогда для этой группы наблюдений в качестве диагональных элементов

l "

матрицы S−1 можно взять 1 sl .

В методе ГолдфельдаÑКвандта требуется дополнительно получить оценку дисперсии для пропущенной средней части наблюдений.Эту оценку можно получить непосредственнопоостаткампропущенныхналюденийиликаксреднее (s21 +s22)/2.

Если точный вид гетероскедастичности неизвестен,и,как следствие,взвешенный МНК неприменим,то,по крайней мере,следует скорректировать оценку ковариационной матрицы оценок параметров,оцененных обычным МНК,прежде чем проверять гипотезы о значимости коэффициентов. (Хотя при использовании обычного МНК оценки будут менее точными,но как ужеупоминалось,они будут несмещенными и состоятельными.)Простейший метод коррекции состоит в замене неизвестной ковариационной матрицы ошибок σ2Ω на ее оценку S 2,где S 2 Ñдиагональная матрица с типичным элементом e2i (т.е.квадратыостатковиспользуются как оценки дисперсий).Тогда получается следующая скорректированная оценка ковариацион-

ной матрицы a (оценка Уайта или устойчивая к гетероскедастичности оценка):

(Z "Z )−1 Z "S 2Z (Z "Z )−1 .

8.3.Автокорреляция ошибок

Если матрица ковариаций ошибок не является диагональной,то говорят об автокорреляции ошибок.Обычно при этом предполагают,что наблюдения однородны по дисперсии,и их последовательнос ть имеет определенный смысл и жестко фиксирована.Как правило,такая ситуация имеет место,если наблюдения проводятся в последовательные моменты времени.В этом случае можно говорить о зависимостях ошибок по наблюдениям,отстоящим друг от друга на 1, 2, 3 и т.д. моментавремени.Обычнорассматривается частныйслучайавтокорреляции,когда коэффициенты ковариации ошибок зависят только от расстояния во времени между наблюдениями;тогда возникает матрица ковариаций,в которой все элементы каждой диагонали(не только главной)одинаковы 1.

Рис. 8.5

шую сторону,при отрицательнойÑв большую сторону.Эти факты подтверждаются тем,что при больших N справедливо следующее соотношение:

где r Ñоценка коэффициента авторегрессии.

Минимального значения величина dc достигает,если коэффициент авторегрессии равен +1.В этом случае ei = e, i = 1, . . . , N , и dc = 0.Если коэффициент авторегрессии равен −1 и ei = (−1)ie, i = 1, . . . , N ,то величина dc достигает

значения 4 NN− 1 (можно достичь и более высокого значения подбором остатков),

которое с ростом N стремится к 4.Формула(8.4)следует непосредственно из(8.3) после элементарных преобразований:

поскольку первое и третье слагаемые при больших N близки к единице,а второе слагаемое является оценкой коэффициента автокорреляции(умноженной на −2).

Известно распределение величины d,если ρ = 0 (это распределение близко к нормальному),но параметры этого р аспределения зависят не только от N и n, как для t- и F -статистик при нулевых гипотезах. ПоложениеÇколоколаÈфункции плотности распределения этой величины зависит от характера Z .Тем не менее, ДарбиниУотсонпоказали,чтоэтоположениеимеетдвекрайниепозиции(рис.8.5).

Поэтому существует по два значения для каждого(двустороннего)квантиля, соответствующего определенным N и n:его нижняя dL и верхняя dU границы. Нулевая гипотеза H0: ρ = 0 принимается,если dU ! dc ! 4 −dU ;она отвергается в пользу гипотезы о положительной автокорреляции,если dc < dL ,и в пользу

DW-критерия).

Пусть нулевая гипотеза отвергнута.То гда необходимо дать оценку матрицы Ω.

Оценка r параметра авторегрессии ρ может определяться из приближенного равенства,следующего из (8.4):

dc r ≈ 1 − 2 ,

или рассчитываться непосредственно из регрессии e на него самого со сдвигом на одно наблюдение с принятиемÇкруговойÈгипотезы,которая заключается в том, что eN +1 = e1.

Для преобразования в пространстве наблюдений,называемом в данном случае авторегрессионным,используют обычно указанную матрицу без1-й строки, что ведет к сокращению количества наблюдений на одно.В результате такого преобразования из каждого наблюдения,н ачиная со2-го,вычитается предыдущее, умноженное на r,теоретическими остатками становятся η ,которые,по предположению,удовлетворяют гипотезе g4.

8.4.Ошибки измерения факторов

Пусть теперь нарушается гипотеза g2,и независимые факторы наблюдаются с ошибками.Предполагается,что изучае мая переменная зависит от истинных значений факторов(далее в этом пункте используется сокращенная форма уравнения регрессии), zö0,а именно:

xö = zö0α + ε,

но истинные значения неизвестны,а вместо этого имеются наблюдения над некоторыми связанными с zö0 переменными zö:

блюдениям(т.е.,в зависимости от контекста, εz обозначает вектор или матрицу ошибок).

Предполагается,что ошибки факторов по математическому ожиданию равны нулю,истинныезначениярегрессоровиошибкинезависимыдруготдруга(покрайней мере не коррелированы друг с другом)и известны матрицы ковариации:

Важно отметить,что эти матрицы и ве ктора ковариации одинаковы во всех наблюдениях,а ошибки в разных наблюдениях не зависят друг от друга,т.е.речь, фактически,идет оÇматричнойÈгомоскедастичности иотсутствии автокорреляции ошибок.

Через наблюдаемые переменные xö и zö уравнение регрессии записывается

В такой записи видно,чтоÇновыеÈостатки не могут быть независимыми от факто- ров-регрессоров zö,т.е.гипотезы основной модели регрессии нарушены.В рамках