
Пластинаның созылусыз, сығылу мен орталық беттің жылжуының шамалы иілуі.
Кирхгоф-Ляв гипотезінің қолданылуы
Қалыңдықтың
төрттен бір бөлігінен кіші
 майысу кезіндегі жіңішке пластинаның
иілуі қарастырылады. Жоғарыда айтылғандай,
мұндай пластиналарқатты
пластиналар деп
ататлады. Кейде оларды орташа қалыңдықтағы
немесе Б.Г. Галеркин терминологиясы
бойынша «жіңішке тақта» деп те атайды.
Иілу теңдеуін алу Кирхгоф-Ляв гипотезіне
негізделген.
майысу кезіндегі жіңішке пластинаның
иілуі қарастырылады. Жоғарыда айтылғандай,
мұндай пластиналарқатты
пластиналар деп
ататлады. Кейде оларды орташа қалыңдықтағы
немесе Б.Г. Галеркин терминологиясы
бойынша «жіңішке тақта» деп те атайды.
Иілу теңдеуін алу Кирхгоф-Ляв гипотезіне
негізделген.
Алғашқы гипотеза, жалпақ қима гипотезасы көлденең жылжудың болмауын болжамдайды, яғни орталыққа параллель қабаттардың өзара жылжуы. Бұл деформация тензорының компоненттеріне шектеу қояды:
 (2.1)
(2.1)
 (2.2)
(2.2)
Кошидің (1.4) геометриялық арақатынастарына сәйкес (2.1) және (2.2) теңдеулері мына түрде жазылуы мүмкін:
 (2.3)
(2.3)
 (2.4)
(2.4)
Интегралдан кейін:
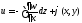

Үшінші
гипотеза себебінен майсу
 көлденең координатасына байланысты
емес, яғни
көлденең координатасына байланысты
емес, яғни ,
сондықтан
,
сондықтан
 (2.5)
(2.5)
 (2.6)
(2.6)
 кезіндегі
орталық бетіндегі нүктелерде
кезіндегі
орталық бетіндегі нүктелерде
 және
және болады. Орталық бетте созылу, сығылу
және жылжу деформациясы жүрмейтіндіктен,
онда оның нүктелерінің ауысуы да
болмайды. Бұл
болады. Орталық бетте созылу, сығылу
және жылжу деформациясы жүрмейтіндіктен,
онда оның нүктелерінің ауысуы да
болмайды. Бұл кезінде
кезінде және осыған орай
және осыған орай болатынын білдіреді. Ақырында, тангенциалды
ауысу мына түрде болады:
болатынын білдіреді. Ақырында, тангенциалды
ауысу мына түрде болады:
 (2.7)
(2.7)

Кернеуді анықтау.
 кернеуіне
сәйкес Кирхгоф-Лявтің екінші гипотезін
қолданамыз. Физикалық арақатынас
негізінде (1.3) мынаны жазуға болады:
кернеуіне
сәйкес Кирхгоф-Лявтің екінші гипотезін
қолданамыз. Физикалық арақатынас
негізінде (1.3) мынаны жазуға болады:

немесе

Соңғы арақатынастан алатынымыз:
 (2.9)
(2.9)
Мұнда
қарама-қайшылық пайда болады. Үшінші
гипотезаға сәйкес майысу көлденең
координатаға байланысты емес,яғни,
 ,
осыған орай,
,
осыған орай, туындысы нөлге тең болуы керек. Бұл
(2.9) формуласымен келіспейді. Бұл
үйлесімсіздік Кирхгоф-Ляв гипотезінің
қарама-қайшылықтарының бірі болып
табылады. Ол шешім кезінде аса қателіктерге
әкелмейді және онымен келісуге тура
келеді. Осылай,
туындысы нөлге тең болуы керек. Бұл
(2.9) формуласымен келіспейді. Бұл
үйлесімсіздік Кирхгоф-Ляв гипотезінің
қарама-қайшылықтарының бірі болып
табылады. Ол шешім кезінде аса қателіктерге
әкелмейді және онымен келісуге тура
келеді. Осылай, деп есептейміз.
деп есептейміз. және
және тангенциалды ауысу арқылы
тангенциалды ауысу арқылы алып, физикалық арақатынастан
алып, физикалық арақатынастан кернеуін аламыз (1.3).
кернеуін аламыз (1.3).

 қоя
отырып, қарапайым өзгерістерден кейін
алатынымыз:
қоя
отырып, қарапайым өзгерістерден кейін
алатынымыз:
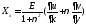 (2.10)
(2.10)
Ұқсастығына қарай
 (2.11)
(2.11)
 (2.12)
(2.12)
(2.10)-(2.12)
арақатынасына (2.7), (2.8)- ден
 жанама ауысуын қоя отырып,
жанама ауысуын қоя отырып, кернеуі үшін ақырға түрін аламыз:
кернеуі үшін ақырға түрін аламыз:

 (2.13)
(2.13)

Қайтадан
 бірінші гипотезаға ораламыз. Гук заңына
сәйкес
бірінші гипотезаға ораламыз. Гук заңына
сәйкес
 (2.14)
(2.14)
 (2.15)
(2.15)
Екінші
гипотеза бойынша
 кернеуі жоқ. Осылай, орталық қабатына
перпендикуляр бағытталған тензор
кернеуінің барлық компоненттері нөлге
тең. Бұл тағы да қарама-қайшылыққа
әкеледі.пластина көлденең кернеумен
жүктелген, бірақ оның әрекеті сәйкес
ішкі күштерді шақырмайды. Пластинаның
тепе-теңдік шарты бұзылады. Осыдан кем
дегенде
кернеуі жоқ. Осылай, орталық қабатына
перпендикуляр бағытталған тензор
кернеуінің барлық компоненттері нөлге
тең. Бұл тағы да қарама-қайшылыққа
әкеледі.пластина көлденең кернеумен
жүктелген, бірақ оның әрекеті сәйкес
ішкі күштерді шақырмайды. Пластинаның
тепе-теңдік шарты бұзылады. Осыдан кем
дегенде кернеуі нөлге тең емес деген қортынды
шығарамыз. Оларды массалық күштер жоқ
алғашқы екі тепе-теңдік теңдеуінен
(1.1) табамыз.
кернеуі нөлге тең емес деген қортынды
шығарамыз. Оларды массалық күштер жоқ
алғашқы екі тепе-теңдік теңдеуінен
(1.1) табамыз.

 .
.
Мұнда
(2.13)-тен
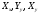 кернеуін қоя отырып, мынаны аламыз
кернеуін қоя отырып, мынаны аламыз

 ,
,
немесе, интеграциялағаннан кейін

 (2.16)
(2.16)
(1.2)
Статистикалық шекаралық шарттарда
 және
және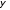 белгісіз функциялары жатыр.
белгісіз функциялары жатыр.
Статистикалық шекаралық шарттардың орындалуы
Үлестірілген көлденең жүктеме пластинаның екі бетінде де жүр деп болжамдаймыз (2.2-сурет).
 кезіндегі
жоғарғы жазықтықта:
кезіндегі
жоғарғы жазықтықта:
 ;
;

 кезіндегі
пластинаның төменгі бетінде:
кезіндегі
пластинаның төменгі бетінде:
 ;
;
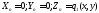
Осы
мәліметтерді (1.2) теңдеуіне қоя отырып,
 кезінде мынаны аламыз:
кезінде мынаны аламыз:
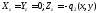 (2.17)
(2.17)
 кезінде:
кезінде:
 (2.18)
(2.18)
 және
және
 белгісіз функциялары (2.17) және (2.18) есепке
ала отырып, мындай түрде болады:
белгісіз функциялары (2.17) және (2.18) есепке
ала отырып, мындай түрде болады:


Бұл
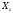 және
және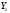 кернеуінің тензор компонентінің ақырғы
түрін жазуға мүмкіндік береді
кернеуінің тензор компонентінің ақырғы
түрін жазуға мүмкіндік береді
 (2.19)
(2.19)
 (2.20)
(2.20)
(2.13),
(2.19) және (2.20) арақатынасы пластинаның
қалыңдығы бойынша кернеудің үлестірілуін
бағалауға мүмкіндік береді. Орталық
қабатының деңгейінде нөлге айнала
отырып және пластинаның беттерінде
экстремалды мәндерге ие бола отырып
 кернеуі сызықтық заң бойынша үлестіріледі,
яғни
кернеуі сызықтық заң бойынша үлестіріледі,
яғни кезінде.
кезінде. және
және кернеуі квадраттық заң бойынша
үлестіріледі. олар орталық қабат
деңгейінде максималды мәндерге ие
болады, ал нөлге
кернеуі квадраттық заң бойынша
үлестіріледі. олар орталық қабат
деңгейінде максималды мәндерге ие
болады, ал нөлге кезінде айналады.
кезінде айналады.
3-дәріс.
Ішкі күш және моменттер
Интегралды сипаттамаларды қарастыруға енгіземіз

 (3.1)
(3.1)


 (3.2)
(3.2)
 -
мембранды күштер,
-
мембранды күштер,
 -
көлденең күштер.
-
көлденең күштер.
Мембранды
күштер пластинаның ортаңғы қабатына
келтірілген созылымды, сығылыңқы және
жылжымалы күштерге ие. (3.1), (3.2)-ден көріп
отырғанымыздай, енгізілген күштік
факторлар
 өлшем бірлігіне ие, яғни ішкі күштің
қарқындылығын сипаттайды.
өлшем бірлігіне ие, яғни ішкі күштің
қарқындылығын сипаттайды.
Интегралды сипаттамадағы тағы бір топ:

 (3.3)
(3.3)

 -
ішкі иілген моменттер
-
ішкі иілген моменттер
 -
айналғыш момент.
-
айналғыш момент.
Өзінің
өлшем бірлігіне сәйкес
 ,
немесе
,
немесе бұл шамалар ішкі моменттердің қарқындылығын
сипаттайды.
бұл шамалар ішкі моменттердің қарқындылығын
сипаттайды.
Осылай енгізілген интегралды сипаттамалар басқаша жалпыланған күштер және моменттер деп аталады. Олардың барлығы пластинаның орталық қабатына келтірілген және олардың әрекеті 3.1-суретінде көрсетілген.

3.1-сурет
Келесідей белгілеулерді енгіземіз:
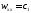
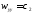 (3.4)
(3.4)

 -
-
 және
және координаталық сызығы бойындағы орталық
қабат қисығының өзгерісін сипаттайтын
параметрлер.
координаталық сызығы бойындағы орталық
қабат қисығының өзгерісін сипаттайтын
параметрлер.
 -
орталық қабаттың бұралу параметрі
-
орталық қабаттың бұралу параметрі
Осы белгілеулерді және (2.13), (2.19) және (2.20) арақатынасын есепке ала отырып жалпыланған күштер мен моменттердің формуласын жазамыз және олардың мәнін есептейміз.
Мембранды күштер:



 мембранды
күштер нөлге тең. Бұл пластинаның орталық
жалпақтығында созылу, сығылу және жылжу
деформациясының болмауы туралы алғашқы
болжамға сәйкес келеді.
мембранды
күштер нөлге тең. Бұл пластинаның орталық
жалпақтығында созылу, сығылу және жылжу
деформациясының болмауы туралы алғашқы
болжамға сәйкес келеді.
Жалпыланған моменттер:



Белгілеулер енгіземіз:

 (3.5)
(3.5)
 -
пластинаның иілуге қарсы тұру қасиетін
сипаттайтын пластинаның иілу (цилиндрлік)
қаттылығы.
-
пластинаның иілуге қарсы тұру қасиетін
сипаттайтын пластинаның иілу (цилиндрлік)
қаттылығы.
Материалдардың
қарсы тұруы курсынан білетініміздей,
бірлік жалпақтықтағы тікбұрышты көлденең
қима балкасы үшін иілу қаттылығы (3.4)
салыстырылатын
 шамасымен анықталады. Пластинаны бірлік
жалпақтықтағы, бір-бірімен бүйір бетімен
байланысқан көптеген балкалардың
жиынтығы түрінде қарауға болады.
шамасымен анықталады. Пластинаны бірлік
жалпақтықтағы, бір-бірімен бүйір бетімен
байланысқан көптеген балкалардың
жиынтығы түрінде қарауға болады.
Балкалардың
әрекеттесуі пластинаның иілу қаттылығы
(3.4) формуласындағы
 көбейткіші арқылы есептелінеді.
көбейткіші арқылы есептелінеді.
(3.4) есепке ала отырып, жалпыланған моменттер мына түрде жазылады:

 (3.6)
(3.6)

Көлденең күштер:
 ,
или
,
или

 (3.7)
(3.7)
Пластинаның тепе-теңдік теңдеуі.
Алғашқы
(1.1) екі тепе-теңдік теңдеуі (2.19), (2.20)
майысу арқылы
 кернеуін жылжыту формуласында
пайдаланылды. Массалық күштің қатысуынсыз
үшінші тепе-теңдік теңдеуін қарастырайық:
кернеуін жылжыту формуласында
пайдаланылды. Массалық күштің қатысуынсыз
үшінші тепе-теңдік теңдеуін қарастырайық:

Жанама кернеудің жұптық заңын есепке ала отырып ол мына түрде жазылуы мүмкін:

Пластинаның қалыңдығы бойынша оны интегралдаймыз:

Бірінші және екінші қосылғыштарды өзгертеміз:


Үшінші қосылғыш.
 ,
,
Мұндағы
 – пластинаның жоғарғы және төменгі
беттерінде әрекет ететін сыртқы жиынтық
жүктеменің қарқындылығы (2.2 сурет).
– пластинаның жоғарғы және төменгі
беттерінде әрекет ететін сыртқы жиынтық
жүктеменің қарқындылығы (2.2 сурет).
Осылай, қалыңдығы бойынша интегралданғаннан кейін тепе-теңдіктің үшінші теңдеуі мына түрде болады:
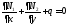 (3.8)
(3.8)
 және
және
 орнына олардың мәндерін қоя отырып,
алатынымыз:
орнына олардың мәндерін қоя отырып,
алатынымыз:
 ,
,
немесе
 (3.9)
(3.9)
Толық түрі:
 , (3.10)
, (3.10)
мұндағы


(3.9) немесе (3.10) теңдеуі – жіңішке пластинаның шамалы иілуіне негізгі рұқсат беретін теңдеу. Ол келесідей қасиеттерге ие:
Сызықтылық (геометриялық арақатынастың сызықтылық нәтижесі);
 координаталарының
ауыстырылуына қатысты инварианттылық.
Бұл материалдың изотроптылық нәтижесі.
координаталарының
ауыстырылуына қатысты инварианттылық.
Бұл материалдың изотроптылық нәтижесі.
(3.9) теңдеуі 1815 жылы Софи Жермен деген француздықтан алынған және оның атымен аталған.
(3.9)
теңдеуінен
 майысу функциясын тапқаннан кейін
пластинаның еркін нүктесіндегі
кернеулі-деформациаланған жағдайдың
барлық компоненттерін анықтауға болады.
Сонымен қатар, бұл теңдеудің шешімі
анықтауға тиісті интегралдау константасының
шығуына әкеледі. Олардың табылуы шеттік
шарттардың қолданылуымен орындалады.
майысу функциясын тапқаннан кейін
пластинаның еркін нүктесіндегі
кернеулі-деформациаланған жағдайдың
барлық компоненттерін анықтауға болады.
Сонымен қатар, бұл теңдеудің шешімі
анықтауға тиісті интегралдау константасының
шығуына әкеледі. Олардың табылуы шеттік
шарттардың қолданылуымен орындалады.
Пластина сұлбасында бекітудің келесідей негізгі түрлері жүзеге асуы мүмкін.
Топсалы бекіту
Егер
 сұлба аймағында пластина топсалы
бекітілсе, онда бұл аймақта майысу және
иілу моменттері болмайды:
сұлба аймағында пластина топсалы
бекітілсе, онда бұл аймақта майысу және
иілу моменттері болмайды: .
аз майысу жағдайында пластиналар тіректе
бос жатқан сұлба үшін шарттар ұқсас
тұжырымдалады.
.
аз майысу жағдайында пластиналар тіректе
бос жатқан сұлба үшін шарттар ұқсас
тұжырымдалады.
Қатты қысылған
Бұл
жағдайда сұлбаның сәйкес аймағында
 майысу болмайды, ал сұлбаға ішкі нормаль
пластина жазықтығына перпендикуляр
жазықтыққа бұрылмайды, яғни
майысу болмайды, ал сұлбаға ішкі нормаль
пластина жазықтығына перпендикуляр
жазықтыққа бұрылмайды, яғни .
.
Бос шет
Егер пластина сұлбасының бірнеше аймағы бос болса, онда шекаралық шарттар бұл аймақта сыртқы күштер әсерлерінің болмауынан анықталады.
Пластинаның
иілуі (3.9) теңдеуіне сәйкес шекаралық
шарттарды
 майысу функциясына және оның туындыларына
шектеу қою арқылы тұжырымдаған ыңғайлы.
Бұл талапқа тек қатты қысу шарты ғана
сәйкес келеді.
майысу функциясына және оның туындыларына
шектеу қою арқылы тұжырымдаған ыңғайлы.
Бұл талапқа тек қатты қысу шарты ғана
сәйкес келеді.
4-дәріс.
Пластина сұлбасындағы шеттік шарттар анықтамасы.
 қалыңдықтағы
пластинаның еркін көрінісін және кейбір
түрдегі бекітулерді қарастырайық.
Сұлбаның қарапайым аймағын белгілеп
алайық. Осы аймақтың кейбір нүктелерімен
екі координаталық жүйені байланыстырамыз.
Олардың бірі
қалыңдықтағы
пластинаның еркін көрінісін және кейбір
түрдегі бекітулерді қарастырайық.
Сұлбаның қарапайым аймағын белгілеп
алайық. Осы аймақтың кейбір нүктелерімен
екі координаталық жүйені байланыстырамыз.
Олардың бірі
 -
негізгі, екіншісі
-
негізгі, екіншісі оның осьтері аймақтың таңдалған
нүктесіндегі
оның осьтері аймақтың таңдалған
нүктесіндегі жанама және
жанама және нормальді бірлік векторларына параллель
және сәйкесінше негізгі жүйе осьтеріне
қатысты
нормальді бірлік векторларына параллель
және сәйкесінше негізгі жүйе осьтеріне
қатысты бұрышына бұрылған етіп құрылған
(4.1-сурет).
бұрышына бұрылған етіп құрылған
(4.1-сурет).

4.1-сурет
Пластинаның
еркін нүктесінде цилиндр бетінің
элементін құрамыз. Осы нүктенің
төңірегіндегі негізгі координата
жүйесінің осьтеріне перпендикуляр
алаңда күш жағдайы
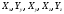 күш тензоры компоненттерімен анықталады.
күш тензоры компоненттерімен анықталады. перпендикуляр ось алаңында күш тензоры
компоненттері екінші ранг тензор
компонентін қайта құру үшін сәйкес
белгілі формулалармен жазылуы мүмкін.
перпендикуляр ось алаңында күш тензоры
компоненттері екінші ранг тензор
компонентін қайта құру үшін сәйкес
белгілі формулалармен жазылуы мүмкін.

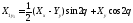 (4.1)
(4.1)

Пластина қалыңдығы бойынша (4.1) арақатынасын интегралдайық. Алғашұы екеуі мембранды күштерді анықтауға мүмкіндік береді.
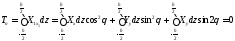

 мембранды
күштері арқылы (3.1) нөлге тең деп
көрсетілгендіктен,
мембранды
күштері арқылы (3.1) нөлге тең деп
көрсетілгендіктен,
 және
және мембранды күштері нөлге тең. Үшінші
теңдеуден
мембранды күштері нөлге тең. Үшінші
теңдеуден перпендикуляр осьі алаңындағы көлденең
күшті аламыз.
перпендикуляр осьі алаңындағы көлденең
күшті аламыз.
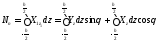 .
.
(3.2)
есепке ала отырып,
 көлденең күші үшін формула мына түрде
болады:
көлденең күші үшін формула мына түрде
болады:
 . (4.2)
. (4.2)
Алғашқы
екі арақатынасты (4.1) және
 көбейте және қалыңдығы бойынша интегралдай
отырып, цилиндр бетінің белгіленген
элементінде иілетін және айналатын
моменттер аламыз.
көбейте және қалыңдығы бойынша интегралдай
отырып, цилиндр бетінің белгіленген
элементінде иілетін және айналатын
моменттер аламыз.
 (4.3)
(4.3)
 (4.4)
(4.4)
Мұндағы
 ,
ал
,
ал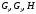 сәйкес (3.3) есептеледі.
сәйкес (3.3) есептеледі.
 -
цилиндрлік бет элементінде әрекет
ететін және
-
цилиндрлік бет элементінде әрекет
ететін және
 жанама векторының айналасында осы
элементті бұруға ұмтылушы иілетін
момент.
жанама векторының айналасында осы
элементті бұруға ұмтылушы иілетін
момент. -
- нормаль векторының айналасындағы
элемент бетін бұратын айналатын момент.
нормаль векторының айналасындағы
элемент бетін бұратын айналатын момент. -
- осьі бағытында әрекет ететін көлденең
күш. Сонымен бірге
осьі бағытында әрекет ететін көлденең
күш. Сонымен бірге мен
мен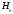 моменттері және
моменттері және көлденең күші сәйкес
көлденең күші сәйкес сыртқы моменттермен және көлденең
күшімен беттесуге ұмтылады. Осылай
пластина сұлбасында келесідей шарттар
орындалуы керек:
сыртқы моменттермен және көлденең
күшімен беттесуге ұмтылады. Осылай
пластина сұлбасында келесідей шарттар
орындалуы керек:
 (4.5)
(4.5)
Есептің орынды қойылымы платина сұлбасының аймағындағы тек екі шеттік шартты тапсырманы талап етеді. Үш шарттың ішінен (4.5) тек екеуі ғана тәуелсіз. Екінші және үшінші шарттар (4.5) біреуімен алмастырыла алады.
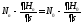 (4.6)
(4.6)
Оған бірінші шартты қосу қажет(4.5)
 (4.7)
(4.7)
(4.6), (4.7) шеттік шарттары – пластина сұлбасындағы Кирхгофтың статистикалық шеттік шарттары деп аталады.
Кирхгоф шартының жүзеге асу мысалы.
Сұлбасында шекаралық шарттың үш түрі жүзеге асырылған тікбұрышты пластинаны қарастырайық (4.2-сурет).

4.2-сурет
Пластинаның сол жақ шеті қатты қысылған.
 (4.8)
(4.8)
 сыртқы
нормальінің векторы абсцисса осьіне
параллель, сол себепті
сыртқы
нормальінің векторы абсцисса осьіне
параллель, сол себепті
 шарты
шарты түрінде жазылады.
түрінде жазылады.
Абсцисса осьіне параллель шеттерінде пластина топсалы бекітілген.

Сұлбаның
осы аймақтары үшін абсцисса осьі мен
сыртқы нормаль векторының арасындағы
бұрыш ( бұрышы)
бұрышы) тең, онда (4.3) формуласынан шығатындай,
тең, онда (4.3) формуласынан шығатындай,

 иілетін
моменттің болмауын
иілетін
моменттің болмауын
 түрінде жазуға болады, ал шеттері
түрінде жазуға болады, ал шеттері болғандықтан тік сызықты болып қалады,
онда
болғандықтан тік сызықты болып қалады,
онда шартынан
шартынан екендігі шығады.
екендігі шығады.
Осылай, топсалы бекітудің ақырғы шарты мына түрде жазылады:
 (4.9)
(4.9)
Егер
топсалы бекіту
 осьіне параллель шетінде жүзеге асса,
онда
осьіне параллель шетінде жүзеге асса,
онда шартын
шартын шартымен ауыстыру қажет.
шартымен ауыстыру қажет.
Пластинаның оң жақ шеті бос

Сұлбаның
бұл аумағында
 жанама векторы ордината осьіне параллель,
сондықтан
жанама векторы ордината осьіне параллель,
сондықтан .
.
Иілу
моменті
 болғандықтан, онда (4.9) сәйкес
болғандықтан, онда (4.9) сәйкес .
Бұрыш
.
Бұрыш =0
екендігін ескере отырып, (4.2) және (4.4)
есептегенде
=0
екендігін ескере отырып, (4.2) және (4.4)
есептегенде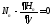 шартын мына түрде қайта жазуға болады
шартын мына түрде қайта жазуға болады
 .
.
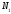 және
және
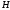 орын ауыстыруынан кейін олардың мәндері
(3.7) және (3.6) бұл формула оңай келесі
түрге көшеді:
орын ауыстыруынан кейін олардың мәндері
(3.7) және (3.6) бұл формула оңай келесі
түрге көшеді:
 ,
,
немесе

Пластинаның бос аумағындағы шекаралық шарттаррдың ақырғы түрі келесідей:
 (4.10)
(4.10)
Егер
пластинаның бос шеті абцисса осьіне
параллель болса, онда (4.10) арақатынастарында
 және
және координаталары орындарымен ауысады.
координаталары орындарымен ауысады.
1-мысал. Көлденең күштегі тікбұрышты пластина иілімі
Сұлбасы
бойынша топсалы бекітілген,
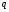 интенсивті көлденең күшпен жүктелген
тікбұрышты пластина. (4.3- сурет).
интенсивті көлденең күшпен жүктелген
тікбұрышты пластина. (4.3- сурет).

4.3-сурет.
Интенсивті синусоидалы заңмен ауысады:
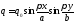 . (4.11)
. (4.11)
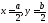 кезінде
пластина ортасында максималды қысым
болады. Бұл нүктеде интенсивтілік
кезінде
пластина ортасында максималды қысым
болады. Бұл нүктеде интенсивтілік
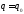 болады. Софи Жермен теңдеуі мына түрде
жазылады:
болады. Софи Жермен теңдеуі мына түрде
жазылады:
 (4.12)
(4.12)
Сұлбасы бойынша пластина топсалы бекітілгендіктен, шекаралық шарттар мына түрде болады:

 (4.13)
(4.13)
(4.12) теңдеуінің шешімін формуланың оң жақ белгісінен іздейміз, яғни
 (4.14)
(4.14)
(4.14)
түрінде жазылған иілу функциясы пластина
деформациясына және шекаралық шарттар
сипатына (4.13) сай келеді. Иілу амплитудасы
пластина орталығында
 анықталуға тиісті. (4.14) иілу функциясын
алмастырып қойғаннан кейін (4.12) теңдеуіне
және тригонометриялық көбейткіштерге
қысқарта отырып,
анықталуға тиісті. (4.14) иілу функциясын
алмастырып қойғаннан кейін (4.12) теңдеуіне
және тригонометриялық көбейткіштерге
қысқарта отырып,
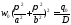
аламыз.
Иілу амплитудасы
 . (4.15)
. (4.15)
(4.15) есепке алғанда (4.14) шешімі мына түрде болады:
 (4.16)
(4.16)
Егер үлестірілген күштің интенсивтілігі мына түрде болса
 , (4.17)
, (4.17)
Онда майысу функциясы келесі түрде болады:
 (4.18)
(4.18)
Майысу функциясы болған кезде пластинаның кез-келген нүктесінен күштеліп-деформацияланған жағдайдың барлық компонентін анықтауға болады.
6-дәріс.
Серпімділік теориясының жазықтық есебін шығару мысалдары.
Тікбұрышты пластинаның біржақты қысылуы.
Еркін түрде сұлбаға бекітілген тікбұрышты пластинаны қарастырайық (6.1-сурет).

6.1 сурет
Пластинаның орталық жазықтығында
абцисса осі бағытында Т0 интенсивтілігінің
қысатын күші әрекет етеді. Сұлбадың
жүктеулі бөлігіне статикалық шекаралық
шарттарды жазамыз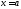 .
.

 (6.1)
(6.1)

Пластинаның қарама қарсы бетіне (
 болғанда) екінші және үшінші шарттар
(1.2) дәл солай жазылады, ал бірінші шарт
мына түрде болады:
болғанда) екінші және үшінші шарттар
(1.2) дәл солай жазылады, ал бірінші шарт
мына түрде болады:
 (6.2)
(6.2)
(5.17) қатынасынан көрінетіндей, бұрылыс
сәті болмағанда кернеу
 .
(6.1) мен (6.2) назарға ала отырып, пластинаның
жүктеулі беттерінен мембранды күш үшін
келесідей формула аламыз
.
(6.1) мен (6.2) назарға ала отырып, пластинаның
жүктеулі беттерінен мембранды күш үшін
келесідей формула аламыз
 (6.3)
(6.3)

Сонымен қатар, жүктеусіз бөлікте

 (6.4)
(6.4)

Мембранды күшті анықтау теңдеуі ,сұлбаны қоса алғанда, пластинаның барлық аумағында орындалады (5.14) Бірінші және екінші теңдеуден көрінетіндей (5.14), (6.3) пен(6.4) есепке алғанда, пластинаның әрбір орталық бөлігіндегі нүкте

 (6.5)
(6.5)

Осылайша, пластинаның барлық ауданы біржақты, бірыңғай қысылу шартында болады.
Пластинаның біркелкі екіжақты қысылуы.
Барлық сұлба бойынша орталық жазықтықты пластина Т0 интенсивті күшінің қысылу іс- әрекетіне ұшырайды ( 6.2 сур).
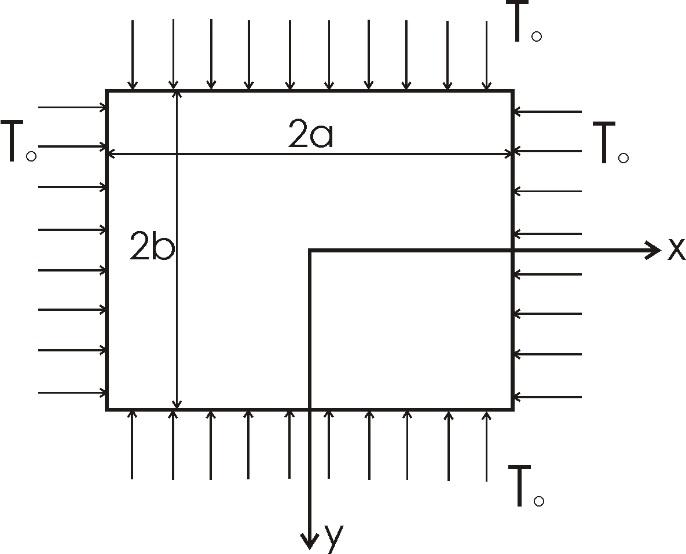
6.2 сурет
Сұлба бөліктеріндегі статикалық
шекаралық шарты (1.2)
 алдыңғы мысалдағыдай (6.1), (6.2) қатынастары
бойынша жазылады.
алдыңғы мысалдағыдай (6.1), (6.2) қатынастары
бойынша жазылады. жағында олар мына түрде болады:
жағында олар мына түрде болады:

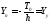 (6.6)
(6.6)

 бетінде бірінші және үшінші шарттар
өзгеріссіз қалады(1.2) , ал екінші мына
түрде жазылады
бетінде бірінші және үшінші шарттар
өзгеріссіз қалады(1.2) , ал екінші мына
түрде жазылады
 (6.7)
(6.7)
Осылайша, (5.17), (6.6) және (6.7) қатынастары
бойынша пластинаның
 бетінде
мембранды күштер (6.3) түрінде жазылады,
ал
бетінде
мембранды күштер (6.3) түрінде жазылады,
ал олар мына түрде болады:
олар мына түрде болады:
 (6.8)
(6.8)

(5.14) тепе- теңдігін дамыта отырып, (6.3) және (6.8) сұлбадағы мембранды күшті есепке алғанда, пластинаның әрбір орталық қабаттарының нүктелері мына түрде болатынын көреміз

 (6.9)
(6.9)

Пластинаның барлық аумағы біркелкі екіжақты қысылу шартында болады.
Пластинаның жылжуы.
Пластинаның сұлбасында
 интенсивтілігінің қозғаушы күші
берілген(6.3 сур).
интенсивтілігінің қозғаушы күші
берілген(6.3 сур).

6.3 сурет
Пластинаның жиегіндегі статикалық
шекаралық шарттарды алдыңғы мысалдар
бойынша анықтай отырып, мембранды күш
үшін формула аламыз.
 бетінде:
бетінде:

 (6.10)
(6.10)
 бетінде:
бетінде:

 (6.11)
(6.11)
Егер пластинаның барлық аумағында
 болса, (5.14) теңдеулері қанағаттанады.
болса, (5.14) теңдеулері қанағаттанады.
Олардың алғашқы екеуі мына түрде жазылады

 (6.12)
(6.12)
Олар
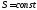 жағдайында бір- біріне қарсы келмейді.
(6.10) мен (6.11) формулаларын ескере отырып,
пластинаның барлық аумағында
жағдайында бір- біріне қарсы келмейді.
(6.10) мен (6.11) формулаларын ескере отырып,
пластинаның барлық аумағында екенін аламыз. Осылайша, пластина
бірыңғай қозғалу шартында орналасады..
екенін аламыз. Осылайша, пластина
бірыңғай қозғалу шартында орналасады..
Тікбұрышты еркін бекітілген пластинаның иілімі (Навье шешімі )
 мен
мен - сұлбаға еркін бекітілген пластина
жақтарының ұзындықтары болсын. Пластина
координаталар жүйесінде 6.4 суреттегідей
орналасқан.
- сұлбаға еркін бекітілген пластина
жақтарының ұзындықтары болсын. Пластина
координаталар жүйесінде 6.4 суреттегідей
орналасқан.

6.4 сурет
Үлестірілген иілім жүктемесінің интенсивтілігі мына түрде берілген
 (6.13)
(6.13)
Онда пластинаның иілген бетінің дифференциалды теңдеуі мына түрге енеді
 (6.14)
(6.14)
Пластина жиектері еркін бекітілгендіктен,
сұлбада иілім
 және иілім сәттері
және иілім сәттері мен
мен нөлге теңелуі керек. Осылайша:
нөлге теңелуі керек. Осылайша:
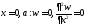
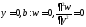 (6.15)
(6.15)
 функциясын қосарлы тригонометриялық
қатар түрінде алайық
функциясын қосарлы тригонометриялық
қатар түрінде алайық
 (6.16)
(6.16)
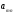 - анықталуы қажет коэффиценттер.
- анықталуы қажет коэффиценттер. қатарынан қандай да бір коэффицентті
табу үшін теңдеудің екі жағын да (6.16)
қатарынан қандай да бір коэффицентті
табу үшін теңдеудің екі жағын да (6.16) көбейтеміз және
көбейтеміз және -ден
-ден -ға дейін біріктіреміз. Келесі
теңдіктерді ескере отырып
-ға дейін біріктіреміз. Келесі
теңдіктерді ескере отырып
 ,
при
,
при ,
,
 ,
при
,
при ,
получаем
,
получаем
 (6.17)
(6.17)
Екі бөлікті де (6.17)
 -ге көбейтеміз және 0 -ден
-ге көбейтеміз және 0 -ден -ға
дейін біріктіреміз. Нәтижесінде келесі
теңдікті аламыз
-ға
дейін біріктіреміз. Нәтижесінде келесі
теңдікті аламыз
 ,
,
осыдан
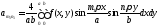 . (6.18)
. (6.18)
(6.18) қатынасы бойынша (6.16) қатарының
барлық коэффиценті анықталады. Берілген
 интенсивтілік жүктемесі синусоидалы
суперпозиция түрінде ұсынылады. Ішінара
синусоидалы жүктеменің әрбірінің иілімі
(4.18) формуласы бойынша анықталады. Толық
иілім сәйкес қосылғыштардың қосындысымен
анықталады және мына түрде жазылады
интенсивтілік жүктемесі синусоидалы
суперпозиция түрінде ұсынылады. Ішінара
синусоидалы жүктеменің әрбірінің иілімі
(4.18) формуласы бойынша анықталады. Толық
иілім сәйкес қосылғыштардың қосындысымен
анықталады және мына түрде жазылады
 (6.19)
(6.19)
Мысал ретінде
 теңдей
үлестірілген интенсивтілік жүктемесі
бар пластина иілімінің есебін қарастырамыз.
Бұл жағдайда
теңдей
үлестірілген интенсивтілік жүктемесі
бар пластина иілімінің есебін қарастырамыз.
Бұл жағдайда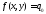 .
. коэффиценттері (6.18) формуласы бойынша
мына түрде жазылады
коэффиценттері (6.18) формуласы бойынша
мына түрде жазылады
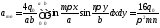 (6.20)
(6.20)
(6.20) формуласында
 мен
мен -
бүтін тақ сандар.
-
бүтін тақ сандар. немесе
немесе коэффициенттері жұп сандар кезінде
коэффициенттері жұп сандар кезінде 0-ге айналады. (6.20)-ны (6.19)-ға ауыстыра
отырып иілімді табамыз:
0-ге айналады. (6.20)-ны (6.19)-ға ауыстыра
отырып иілімді табамыз:
 (6.21)
(6.21)
Мұнда
 Бұл теңдей үлестірілген интенсивтілік
жүктемесі бар пластина иілімі сипатына
сәйкес келеді. Бұл жағдайдаиілген бет
Бұл теңдей үлестірілген интенсивтілік
жүктемесі бар пластина иілімі сипатына
сәйкес келеді. Бұл жағдайдаиілген бет осьтеріне симметриялы болады. Қатардағы
осьтеріне симметриялы болады. Қатардағы мен
мен жұп қосылғыштары (6.21) жоғалуы керек,
себебі олар көрсетілген осьтерге
симметриялы бола алмайды. Ең үлкен иілім
пластинаның ортасында болады және
(6.21) формуласына
жұп қосылғыштары (6.21) жоғалуы керек,
себебі олар көрсетілген осьтерге
симметриялы бола алмайды. Ең үлкен иілім
пластинаның ортасында болады және
(6.21) формуласына мәндерін қою арқылы алынады:
мәндерін қою арқылы алынады:
 (6.22)
(6.22)
Бұл қатар жылдам үйлеседі. Қанағаттанарлық
дәлдік
 болған
кезде- ақ пайда болады. Квадрат пластина
үшін ол
болған
кезде- ақ пайда болады. Квадрат пластина
үшін ол
 (6.23)
(6.23)
немесе, (3.5)формуласы бойынша иілім
қатаңдығы
 кезінде
кезінде
 (6.24)
(6.24)
Бұл мәннің ауытқуы 2,5 пайыз шамасында.
Дөңгелек пластинаның иілімі
Дөңгелек пластинаның иілім есебі полярлы
координат жүйесінде шешіледі. Қарастыруға
 полярлы радиусы мен
полярлы радиусы мен полярлы бұрышын енгізіп,
полярлы бұрышын енгізіп, және
және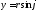 белгілі арақатынастарына сәйкес
алатынымыз:
белгілі арақатынастарына сәйкес
алатынымыз:

Пластина иілімінің теңдеуі мына түрде жазылады:
 (6.24)
(6.24)
Пластина беті бойынша орталыққа қатысты
симметриялы үлестірілген жүктеме жайлы
қарапайым жағдайды қарастырайық. Мұндағы
 ,
яғни майысу
,
яғни майысу полярлы бұрышына байланысты емес. (6.24)
теңдеуі қарапайым түрге енеді
полярлы бұрышына байланысты емес. (6.24)
теңдеуі қарапайым түрге енеді
 (6.25)
(6.25)
Бұл теңдеудің жалпы интегралы мына түрде жазылады
 (6.26)
(6.26)
Оң жақтағы алғашқы төрт қосылғыш біркелкі
теңдеуге сәйкес ортақ шешімді
қалыптастырады, ал
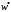 -
(6.25) теңдеуінің жеке шешімі. Біркелкі
үлестірілген жүктеме жағдайында (
-
(6.25) теңдеуінің жеке шешімі. Біркелкі
үлестірілген жүктеме жағдайында ( -
тұрақты)
-
тұрақты)

Пластина ортасында иілімнің шектілігі
мен қисықтығы шартынан (6.26) шешімінен
 деп болжаймыз, ал
деп болжаймыз, ал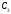 пен
пен тұрақты интегралы пластина сұлбасы (
тұрақты интегралы пластина сұлбасы ( кезінде) шартынан анықталады. Бітелген
аумақ үшін:
кезінде) шартынан анықталады. Бітелген
аумақ үшін:
 (6.27)
(6.27)
Бекітілген аумақ үшін:
 (6.28)
(6.28)
(6.27) шартын орындай отырып, пластина
үшін сұлбамен жасалғанды аламыз
 (6.29)
(6.29)
Сол сияқты, (6.28) есепке ала отырып бекітілген аумақтағы пластина үшін иілімді табамыз
 (6.30)
(6.30)
Иілім формуласы бойынша жүктеменің симметриялы үлестірімі кезінде мына формула бойынша есептелетін, иілу және айналу моменттерінің мәнін есептейміз

8-дәріс
Пластинаның тұрақтылық есебін шешу мысалдары
Бір жақты қысу кезіндегі пластинаның тұрақтылығы
Серпімділік теориясының жазықық есебін
шешу барысындағы пластинаны бір жақты
қысу кезіндегі мембранды күштер
 мәндері (6.5) алынған болсын. Олардың
мәндерін есепке ала отырып, бейтарап
тепе-теңдік теңдеуі (7.14) келесідей түрде
болады:
мәндері (6.5) алынған болсын. Олардың
мәндерін есепке ала отырып, бейтарап
тепе-теңдік теңдеуі (7.14) келесідей түрде
болады:
 (8.1)
(8.1)
Пластинаның шеттері топсалы бекітілген деп есептейік, сондықтан 7.4-суретіне сәйкес шекаралық шарттар келесідей түрде жазылады:

 (8.2)
(8.2)
(8.1) теңдеуінің шешімін келесі формуладан іздейміз
 (8.3)
(8.3)
Мұндағы және
 - толқынды сандар. Олар пластинаның
бойындағы және көлденең бағыттағы
жартылай толқынның санын сипаттайды.
(8.3)-ті (8.1)-ге енгізе отырып дифференциалдау
және тригонометриялық көбейткіштерге
қысқарту операцияларынан кейін мына
теңдеуді аламыз:
- толқынды сандар. Олар пластинаның
бойындағы және көлденең бағыттағы
жартылай толқынның санын сипаттайды.
(8.3)-ті (8.1)-ге енгізе отырып дифференциалдау
және тригонометриялық көбейткіштерге
қысқарту операцияларынан кейін мына
теңдеуді аламыз:
 (8.4)
(8.4)

(8.4)-тен алатынымыз

 және
және толқынды сандардың толық мәндері кезінде
аз қызығушылықтағы сыни күштердің
спектрін аламыз. Келесідей белгілеулерді
енгіземіз:
толқынды сандардың толық мәндері кезінде
аз қызығушылықтағы сыни күштердің
спектрін аламыз. Келесідей белгілеулерді
енгіземіз:
 ,
,
Сонымен қатар, сыни қысушы күшті мына түрде көрсетуге болады
 (8.5)
(8.5)
 -
- және
және екі айнымалысының функциясы. Оның
минимизациясы үшін келесідей шартты
орындау қажет
екі айнымалысының функциясы. Оның
минимизациясы үшін келесідей шартты
орындау қажет
 ,
, (8.6)
(8.6)
(8.6) бірінші шартынан
 екендігі шығады. Екінші шарт
екендігі шығады. Екінші шарт

Бұл
 өскен кезде
өскен кезде күшінің өсетіндігін білдіреді.
күшінің өсетіндігін білдіреді. минимумы
минимумы (
( )
осі бағытындағы бір жарты толқынына
сәйкес келетін
)
осі бағытындағы бір жарты толқынына
сәйкес келетін мәні кезінде жүзеге асады.
мәні кезінде жүзеге асады. шартынан
шартынан шығады. Соңғысы
шығады. Соңғысы кезінде
кезінде пластина қабырғасы қатынасына тең,
пластина қабырғасы қатынасына тең, толқындық санын анықтауға мүмкіндік
береді. Дегенмен,
толқындық санын анықтауға мүмкіндік
береді. Дегенмен,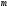 -
бүтін сан, сондықтан бұл шешім
-
бүтін сан, сондықтан бұл шешім кезінде мағынаға ие болады.
кезінде мағынаға ие болады.
 болсын. Бұл жағдайда
болсын. Бұл жағдайда ,
ал
,
ал .
(8.5) есепке ала отырып, сыни қысушы күш
мына түрде болады
.
(8.5) есепке ала отырып, сыни қысушы күш
мына түрде болады
 (8.7)
(8.7)
Сыни кернеу
 (8.8)
(8.8)
Егер
 шеттері бекітілмеген кездегі пластинаның
бір жақты қысылуын қарастыратын болсақ,
онда бұл жағдайда сыни кернеудің шамасы
қысылған стержень үшін Эйлердің сызықтық
теориясы бойынша анықталады.
шеттері бекітілмеген кездегі пластинаның
бір жақты қысылуын қарастыратын болсақ,
онда бұл жағдайда сыни кернеудің шамасы
қысылған стержень үшін Эйлердің сызықтық
теориясы бойынша анықталады.
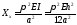 (8.9)
(8.9)
(8.8) және (8.9) формулаларын салыстыру бір жақты қысу кезінде квадратты пластинаның бойлық шеттерінің топсалы бекітілуі сыни кернеудің төрт рет өсуіне әкеледі деген қорытынды шығарады.
Барлық жағынан біркелкі қысу кезіндегі пластинаның тұрақтылығы.
Мембранды күштер (6.9) формуласын есепке ала отырып, бейтарап тепе-теңдік теңдеуі (7.14) бұл жағдайда мына түрде жазылады
 (8.10)
(8.10)
Пластинаның шеттері топсалы бекітілген деп есептейміз, сондықтан шекаралық шарттары (8.2) формасындағыдай жазылады. Мұндай болжам кезінде (8.10) теңдеуі келесі түрге келетінін көрсетуге болады
 (8.11)
(8.11)
Немесе, белгілеуін енгізгеннен кейін
 ,
,
 (8.12)
(8.12)
Дәлелдеу үшін, (8.10) теңдеуін интегралдаймыз.
 (8.13)
(8.13)
аламыз.
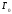 -
үйлесімділік функциясы. Оны анықтау
үшін (8.2) шекаралық шарттарын пайдаланамыз.
-
үйлесімділік функциясы. Оны анықтау
үшін (8.2) шекаралық шарттарын пайдаланамыз. кезінде майысу
кезінде майысу ,
демек,
,
демек, және
және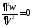 .
Нәтижесінде, пластинаның бұл шеттерінде
шекаралық шарттар мына түрде жазылуы
мүмкін екендігін аламыз:
.
Нәтижесінде, пластинаның бұл шеттерінде
шекаралық шарттар мына түрде жазылуы
мүмкін екендігін аламыз:
 (8.14)
(8.14)
Сәйкесінше пайымдай отырып шекаралық
шарттардың осындай түрі
 шеттерде де болады деп айтуға болады.
Сонымен, (8.13) теңдеудің сол жақ бөлігі,
және сәйкесінше
шеттерде де болады деп айтуға болады.
Сонымен, (8.13) теңдеудің сол жақ бөлігі,
және сәйкесінше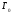 функциясы пластинаның барлық сұлбасында
нөлге айналады. Сонымен қатар, (8.13)
теңдеуі пластинаның сұлбаны қосқандағы
барлық аумағында дұрыс болады. Сөйтіп,
пластинаның кез-келген нүктесінде
функциясы пластинаның барлық сұлбасында
нөлге айналады. Сонымен қатар, (8.13)
теңдеуі пластинаның сұлбаны қосқандағы
барлық аумағында дұрыс болады. Сөйтіп,
пластинаның кез-келген нүктесінде және (8.12) теңдеуі шынымен орны бар. Бұл
теңдеудің шешімін майысу функциясын
мына түрде бер отырып, іздейміз:
және (8.12) теңдеуі шынымен орны бар. Бұл
теңдеудің шешімін майысу функциясын
мына түрде бер отырып, іздейміз:
 (8.15)
(8.15)
(8.12) теңдеуіне
 қоя отырып:
қоя отырып:
 ,
немесе
,
немесе
 (8.16)
(8.16)
аламыз.
 және
және толқынды сандары өсе отырып, сыни қысушы
күш өседі. Квадрат пластина үшін
толқынды сандары өсе отырып, сыни қысушы
күш өседі. Квадрат пластина үшін жақты минималды сыни қысушы күш әрбір
бағыттағы бір жарты толқынның туындауымен
жүзеге асады және мына формула бойынша
анықталады:
жақты минималды сыни қысушы күш әрбір
бағыттағы бір жарты толқынның туындауымен
жүзеге асады және мына формула бойынша
анықталады:
 (8.17)
(8.17)
Сыни кернеу
 (8.18)
(8.18)
(8.8) формуласымен салыстыру пластинаны бір жақты қысу жағдайымен салыстырғанда сыни кернеу екі есе азаятындығын көрсетеді.
Жылжу кезіндегі пластинаның тұрақтылығы.
Серпімділік теориясының жазықтық есебінің сәйкес шешімін ескере отырып, бейтарап тепе-теңдік теңдеуін мына түрде жазамыз
 (8.19)
(8.19)
Шекаралық шарттарды алдыңғы мысалдар сияқты (8.2) формасында қабылдаймыз. (8.19) теңдеуінің шешімін мына түрде іздеуге де болатын:
 (8.20)
(8.20)
Бұл функция толқын жасалу бейнесін жақсы сипаттайды, бірақ ол (8.2) топсалы бекітілудің шекаралық шарттарымен сәйкес келмейді. Сол себепті, майысудың жуықтамасы (8.20) формасында мүмкін емес.
Есепті Бубнов-Галеркин әдісі көмегімен жуықтап шығаратын боламыз. Жуықтама функциясы ретінде келесі формуланы аламыз:
 (8.21)
(8.21)
Мұндағы
 ,
, -
- осі бағытындағы жартылай толқындар
саны,
осі бағытындағы жартылай толқындар
саны, тұрақтылығын жоғалтқаннан кейінгі
пластина бетіндегі толқындардың иілу
бұрышын сипаттайды.
тұрақтылығын жоғалтқаннан кейінгі
пластина бетіндегі толқындардың иілу
бұрышын сипаттайды.
Пластина шеттерінде
 (8.21) функциясы
(8.21) функциясы шартын қанағаттандырады, бірақ
шартын қанағаттандырады, бірақ шартын қанағаттандырмайды.
шартын қанағаттандырмайды. кезінде топсалы бекітудің шекаралық
шарттары орындалмайды. Осы функцияны
жуықтаушы ретінде
кезінде топсалы бекітудің шекаралық
шарттары орындалмайды. Осы функцияны
жуықтаушы ретінде осі бағытында созылған тек пластинаға
қолдануға болады, яғни
осі бағытында созылған тек пластинаға
қолдануға болады, яғни кезінде. Бубнов-Галеркин әдісінің жүзеге
асу кезінде
кезінде. Бубнов-Галеркин әдісінің жүзеге
асу кезінде жылжушы күшін интегралды есептей отырып
анықтаймыз
жылжушы күшін интегралды есептей отырып
анықтаймыз
 (8.22)
(8.22)
 жылжушы күші келесідей функционалды
тәуелділік түрінде көрсетіледі
жылжушы күші келесідей функционалды
тәуелділік түрінде көрсетіледі
 (8.23)
(8.23)
 және
және параметрлері бойынша
параметрлері бойынша минимизациялай отырып сыни жылжушы
күшті мына түрде аламыз
минимизациялай отырып сыни жылжушы
күшті мына түрде аламыз
 (8.24)
(8.24)
Сәйкес сыни кернеу
 (8.25)
(8.25)
