5. Замкнутые и полные ортонормированные системы.

Определение 7. Ортонормированная система {_n} в бесконечномерном евклидовом пространстве называется замкнутой, если любой элемент этого пространства можно приблизить с произвольной точностью по норме данного пространства с помощью конечной линейной комбинации элементов _k.

Иными словами, если .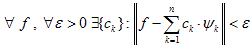

Теорема 6. Необходимое и достаточное условие замкнутости ортонормированной системы. Для того чтобы ортонормированная система {_n} была замкнута, необходимо и достаточно, чтобы для любого элемента

f выполнялось равенство

.

1. Необходимость.

Воспользуемся тождеством Бесселя.

Если система {_n} − замкнутая, то > 0 N такое, что левая часть тождества будет меньше чем при n ≥ N, поэтому

.

2. Достаточность.

Если , то > 0 n такое, что правая часть тождества будет меньше, чем ,

следовательно, и левая часть тождества будет меньше чем . Это означает, что система _n будет замкнутой. 

Глава XIX. Функциональные последовательности и ряды. § 6

Ряды Фурье

Примеры решения задач

1.Запишите ряд Фурье по основной тригонометрической системе функций для функции

.

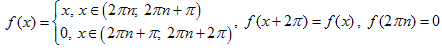
Решение. Коэффициенты Фурье равны

поэтому многочлены Фурье имеет вид

,

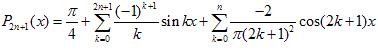
Ряд Фурье

,

сходится равномерно на любом промежутке x [₁; 2− ₂], 0 < ₁ < 2− ₂ < 2, в чем легко убедиться с помощью признака Абеля-Дирихле, поэтому его сумма на указанном множестве равна f(x).

На любом промежутке x (; + ₃), ₃ > 0, равномерная сходимость отсутствует. В этом легко убедиться с помощью критерия Коши. Отсутствие равномерной сходимости на промежутке вида x (; + ₃) вытекает также из теоремы о непрерывности равномерного предела ряда непрерывных функций.

Сумма ряда в точках разрыва f(x) равна , в чем легко убедится

а) подстановкой этого значения переменной,

б) с помощью теоремы о сумме ряда Фурье в точке разрыва кусочно–гладкой функции.

2.Запишите ряд Фурье по основной тригонометрической системе функций для функции f(x) = x, x (−; ), f(x + 2) = f(x), f (+ 2n) = 0.

Решение. Коэффициенты Фурье равны

поэтому ряд Фурье имеет вид

.

Ряд сходится равномерно на любом промежутке x [−+ ₁; − ₂], в чем легко убедиться с помощью признака Абеля-Дирихле, поэтому его сумма на указанном множестве равна f(x).

На любом промежутке x (− ₃; + ₃), ₃ > 0, равномерная сходимость отсутствует. В этом легко убедиться с помощью критерия Коши. Отсутствие равномерной сходимости на промежутке вида x (− ₃; + ₃) вытекает также из теоремы о непрерывности равномерного предела ряда непрерывных функций.

Сумма ряда в точках разрыва f(x) равна 0, в чем легко убедится а) подстановкой этого значения переменной, б) с помощью теоремы о сумме ряда Фурье в точке разрыва кусочно–гладкой функции.