Глава XIX. Функциональные последовательности и ряды. § 3

Свойства равномерно сходящихся функциональных рядов

Примеры решения задач

1.Вычислите .

Решение. Рассмотрим некоторый промежуток. Если ряд сходится равномерно на этом промежутке, то можно переходить к пределу под знаком суммирования и тогда

. Осталось доказать равномерную

сходимость ряда на данном множестве. Более того, можно утверждать, что ряд сходится

равномерно на [0; + ∞). Действительно, x ≥ 0 верно соотношение , а ряд

сходится как геометрическая прогрессия со знаменателем, меньшим по модулю 1.

Следовательно, ряд сходится равномерно по признаку Вейерштрасса и был законным предельный переход.

2.Покажите, что функциональная последовательность равномерно сходится на сегменте [0; 1], но условия теоремы о почленном дифференцировании не

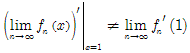
выполнены и .

Решение. Покажем, что последовательность сходится равномерно на

x [0; 1].

Сначала найдем . Так как

, то, согласно практическому

критерию, последовательность сходится равномерно на сегменте [0;1]

Теперь докажем, что равномерная сходимость последовательности f_n^'(x) на сегменте [0; 1] не имеет места.

Найдем f_n^'(x). Для любого номера n .

Найдем предел .

Для оценки воспользуемся неравенством

.

Отсюда .

Согласно практическому критерию, равномерная сходимость последовательности {f_n^'(x₀)} на сегменте [0; 1] не имеет места.

Вычислим и .

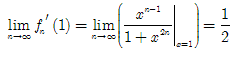
Очевидно, .

Глава XIX. Функциональные последовательности и ряды. § 3

Свойства равномерно сходящихся функциональных рядов

Задачи и упражнения для самостоятельной работы

5.Найти область существования функции и исследовать ее в этой

области на непрерывность.

Ответ: сходится и непрерывна на |x| ≤ 1.

6._{Найти предел}

7.Найти предел

8.Найти область существования функции и исследовать ее во

внутренних точках этой области на дифференцируемость.

9.Покажите, что ряд допускает почленное интегрирование на промежутке

и напишите полученный в результате интегрирования числовой ряд.

Глава XIX. Функциональные последовательности и ряды. § 4

Степенные ряды

Основные понятия

Определение. Степенным рядом называется ряд вида

(1)

1. Понятие степенного ряда.

Теорема 1. Если степенной ряд сходится при x = x₁, то он сходится и притом абсолютно для всех |x| < |x₁|.

Следствие. Если при x = x₁ ряд расходится, то он расходится для всех |x| > |x₁|.

Теорема 2. Если степенной ряд сходится для положительного значения x =

x₁, то он сходится равномерно в любом промежутке внутри (−|x₁|; |x₁|).

Рассмотрим последовательность

(2)

Теорема 3 (Коши-Адамара). Если последовательность (2) не ограничена, то степенной ряд (1) сходится лишь при x = 0.

Если последовательность (2) ограничена и имеет верхний предел L > 0, то ряд (1)

абсолютно сходится для значений x, удовлетворяющих неравенству и

расходится для значений x, удовлетворяющих неравенству .

Если последовательность (2) ограничена и её верхний предел L = 0, то ряд (1) сходится абсолютно для всех значений x R.

Таким образом, для каждого степенного ряда существует такое положительное число R, что при всех х таких, что |x| < R ряд абсолютно сходится, а при всех |x| > R ряд расходится.

Определение. Число R называется радиусом сходимости. Интервал (−R, R) назовем областью сходимости.

Отметим, что множество точек, принадлежащее области сходимости, может быть как замкнутым с одной или двух сторон, так и не замкнутым.

Радиус сходимости может быть найден по формуле:

или по формуле .

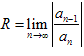
Согласно теореме 2, каково бы ни было положительное число r, удовлетворяющее условию r < R, ряд (1) равномерно сходится на сегменте [−r, r].

Теорема 4. Непрерывность суммы степенного ряда. Сумма степенного ряда внутри его промежутка сходимости является непрерывной функцией.

Теорема 5. Интегрирование степенных рядов. Если некоторая функция f

(x) определяется степенным рядом: , то для всех x, удовлетворяющих

условию |x| < R, интеграл от этой функции можно записать в виде ряда:

,

то есть степенной ряд можно интегрировать почленно. Последний ряд имеет тот же радиус сходимости, что и исходный.

Теорема 6. Дифференцирование степенных рядов. Если некоторая функция

f(x) определяется степенным рядом: , то для всех x, удовлетворяющих

условию |x| < R, её производная находится по формуле:

,

то есть ряд можно дифференцировать почленно. Последний ряд имеет тот же радиус сходимости, что и исходный.

2. Сложение, вычитание, умножение и деление степенных рядов. Пусть R₁ − радиус

сходимости степенного ряда , а R₂ − радиус сходимости степенного ряда

. Обозначим R = min (R₁, R₂).

Сложение и вычитание степенных рядов при всех x, удовлетворяющих условию |x| < R, сводится к соответствующим операциям с их членами:

, где c_n = a_n ± b_n.

Произведение двух степенных рядов при всех x, удовлетворяющих условию |x| < R, выражается формулой:

Коэффициенты с_i находятся по формуле:

с_n = a₀b_n + a₁b_{n − 1} + … + a_{n − 1}b₁ + a_nb₀

Деление двух степенных рядов при всех x, удовлетворяющих условию |x| < R, выражается формулой:

Для определения коэффициентов q_n рассматриваем произведение

, полученное из записанного выше равенства, и решаем

систему уравнений: