Глава XIX. Функциональные последовательности и ряды. § 4

Степенные ряды

Примеры решения задач

1.Найти область сходимости ряда

Решение. Находим радиус сходимости

.

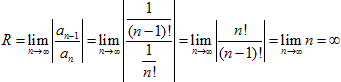
Следовательно, данный ряд сходится при любом значении х.

2._{Найти область сходимости ряда}

(1)

Решение. Находим радиус сходимости .

Следовательно, данный ряд сходится при .

Исследуем поведение ряда в граничных точках интервала сходимости.

Сначала рассмотрим точку . Частичная сумма ряда в этой точке равна

.

Очевидно, . Поскольку последовательность частичных сумм

гармонического ряда расходится, то, согласно признаку сравнения,

последовательность {S_2n} тоже расходится.

Значит, ряд (1) расходится при

Теперь рассмотрим точку

.

. Частична сумма ряда в этой точке равна

Ряд сходится, поэтому сходится и последовательность его частичных

сумм. Гармонический ряд расходится.

Таким образом, последовательность {S_2n} представляет собой сумму сходящейся и расходящейся последовательности, значит {S_2n} расходится, а ряд (1) расходится при

.

3.Применяя почленное дифференцирование вычислить сумму ряда

(2)

Решение. Сначала определим радиус сходимости числового ряда (2)

.

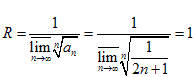
Согласно теореме о дифференцировании степенного ряда, при |x| < 1 имеет место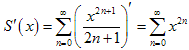

формула .

Применяя формулу суммы бесконечной геометрической прогрессии при |x| < 1,

получаем: . Вычислим . Для однозначного определения

константы интегрирования, воспользуемся значением S(0) = 0.

Окончательно получим: .

4.Разложение в степенной ряд при помощи формулы Маклорена.

Решение. Разложить в ряд функцию .

По формуле Маклорена

, где

Окончательно, получим ряд: f(x) = 1 + x + x² + … + xⁿ + …

Рассмотрим способ разложения функции в ряд при помощи интегрирования.

С помощью интегрирования можно разлагать в ряд такую функцию, для которой известно или может быть легко найдено разложение в ряд ее производной.

Находим дифференциал функции df(x) = f ^'(x)dx и интегрируем его в пределах от 0 до х.

5._{Разложить в ряд функцию f(x) = ln(1 + x).}

Решение. Решим эту задачу при помощи интегрирования.

Так как , f(0) = 0,

получаем по приведенной выше формуле:

.

Разложение в ряд функции можно получить, если рассматривать эту выражение

как сумму бесконечной геометрической прогрессии со знаменателем −x где |x| < 1:

Тогда получаем:

Окончательно получим: