Глава XIX. Функциональные последовательности и ряды. § 4

Степенные ряды

Задачи и упражнения для самостоятельной работы

10.Определите радиус и интервал сходимости ряда и исследуйте поведение в граничных точках интервала сходимости.

10.1.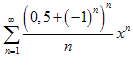

10.2.

10.3.

11._{Применяя почленное дифференцирование, вычислить сумму ряда .}

12._{Применяя почленное интегрирование, вычислить сумму ряда .}

ГЛАВА XIX. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ. § 5

Ряды Тейлора

Основные понятия

Теорема 1. Если функция f(x) определена в некоторой окрестности точки a, и у функции f(x) существуют производные любого порядка в этой точке, то она может быть

представлена рядом .

Определение. Областью сходимости ряда Тейлора с центром разложения в точке a будем называть множество точек x, удовлетворяющих неравенству |x − a| < R, где R называют радиусом сходимости.

Теорема 2.Радиус сходимости для ряда Тейлора определяется по формуле Коши-Адамара:

,

где под c_k в данном случае понимаем .

Напомним, что эта формула верна для любого ряда вида .

Часто используются следующие основные разложения в ряд Тейлора с центром разложения в точке x = 0:

;

.

В случае приближенных вычислений ряд заменяется его частичной суммой

Число n определяется точностью, с которой необходимо провести

вычисления. Оценку точности можно получить по остаточному члену ряда Тейлора, для которого существуют разные формы представления, но наиболее часто используются

остаточный член в форме Лагранжа

или остаточный член в форме Коши:

.

Глава XIX. Функциональные последовательности и ряды. § 5

Ряды Тейлора

Примеры решения задач

1.Найдите радиус сходимости и область сходимости ряда

.

Решение. Воспользуемся формулой Коши-Адамара.

.

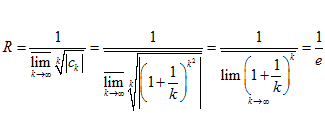
Область сходимости − .

2.Разложите в ряд Тейлора в окрестности точки x = 2 функцию .

Решение. Применим формулу суммы бесконечной геометрической прогрессии

, где a₁ − первый член прогрессии, q − знаменатель прогрессии.

Только на этот раз мы не будем считать сумму прогрессии, а наоборот, от суммы перейдем к ряду.

Действительно, .

Тогда .

3.Разложите в ряд Тейлора с центром в точке x₀ = 0 функцию f(x) = arctg x в ее области сходимости.

Решение. Рассмотрим производную .

Разложим эту функцию в ряд Тейлора, используя сумму прогрессии:

.

Область сходимости этого степенного ряда |x| < 1.

Как известно, степенной ряд сходится равномерно внутри области сходимости, поэтому его можно интегрировать почленно. Проинтегрируем данный ряд и найдем таким

образом разложение для . Константа, возникающая при

интегрировании, равна нулю, так как f(0) = 0.