2. Поточечная сходимость тригонометрического ряда Фурье.

Определение 2. Функция f (x) называется кусочно-непрерывной на сегменте [ a, b ], если она непрерывна во всех точках сегмента [ a, b ] за исключением, быть может, конечного числа точек, в которых она имеет разрыв первого рода.

Определение 3. Кусочно-непрерывная на сегменте [ a, b ] функция называется кусочно-гладкой на этом сегменте, если производная этой функции f ^' (x) существует и непрерывна всюду на сегменте [ a, b ], за исключением, быть может, конечного числа точек, в которых существует правый и левый пределы и .

Лемма 1. Об аппроксимации непрерывной на сегменте [ a,

b ] функции кусочно-гладкой функцией. Пусть функция f (x) непрерывна на сегменте [ a, b ]. Тогда для любого > 0 существует непрерывная, кусочно-гладкая функция l (x), такая, что для любого x из сегмента [ a, b ] выполняется условие |f (x) − l (x)| < , причём l (a) = f (a), l (b) = f (b).

Лемма 2. Если функция f (x) кусочно-непрерывна на сегменте [ a, b ], то

1) при → ∞ ,

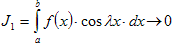
2) при → ∞ .

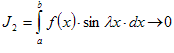
Теорема 2. О поточечной сходимости тригонометрического ряда Фурье. Пусть f (x) – кусочно-гладкая функция на сегменте [ − ; ]. Тогда ряд

, где , ,

,

сходится в каждой точке x [ − ; ], и для его суммы S (x) справедливо равенство

1) ,

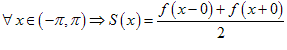
2) .

3. Комплексная форма ряда Фурье. Заметим, что

При этом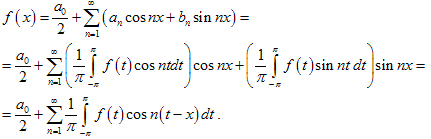

Таким образом,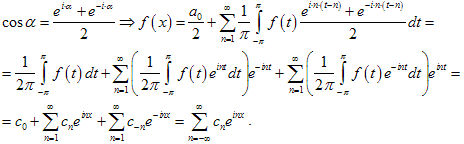

, где .

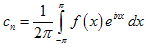
Тем самым мы получили разложение функции f (x) по системе функций {e^inx}. Указанная система функций является ортогональной на сегменте [ − ; ], то есть

.

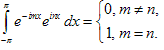
4. Понятие общего ряда Фурье по произвольной ортогональной системе функций. Тригонометрический ряд Фурье является частичным случаем общего ряда Фурье. Рассмотрим пространство кусочно-непрерывных на сегменте [a, b] функций Q[a, b]. Будем предполагать, что в точке разрыва

.

Введём в пространстве Q[a, b] скалярное произведение (свёртку) двух функций,

. Имеет место неравенство Коши

^{(f, g)2} ≤ ^{(f, f) · (g, g).}

Определение 4. Линейное пространство называется нормированным, если каждому элементу f поставлено в соответствие неотрицательное вещественное число − норма, || f ||, которая удовлетворяет следующим условиям:

1. || f || > 0, если f ≠ ; || f || = 0, если f = ,

2. || · f || = || · || f ||, для любого числа ,

3. f, g ||f + g|| ≤ ||f|| + ||g||.

В любом нормированном пространстве можно ввести метрику, т.е. расстояние между двумя элементами, по формуле

(f, g) = || f − g ||.

Во всяком евклидовом пространстве можно ввести норму

.

Определение 5. Последовательность элементов евклидова пространства

{_n} называется ортонормированной, если её элементы попарно ортогональны, а норма каждого элемента равна единице.

Определение 6. Рядом Фурье элемента f по ортонормированной системе

{_n} называется ряд , где f_n = (f, _n). Величины f_n называются коэффициентами Фурье элемента f.

Если евклидово пространство имеет конечную размерность N, то система {_n}, состоящая из N ортогональных элементов, норма каждого из которых равна единице, образует ортонормированный базис и любой элемент f такого пространства можно разложить по этому базису

.

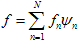
В случае бесконечной размерности евклидова пространства актуален вопрос о сходимости ряда Фурье по метрике данного пространства. Назовем величину

частичной суммой ряда Фурье.

Наряду с S_n будем рассматривать линейные комбинации элементов ортонормированной системы

.

Теорема 3. При фиксированном n из всех сумм вида наименьшее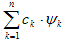

отклонение от элемента f по норме данного евклидова пространства имеет частичная сумма

.

Это свойство называют экстремальным свойством ряда Фурье.

Теорема 4. Для любого элемента f, для любой ортонормированной системы {_n} и для любого n выполняется равенство (тождество Бесселя)

Теорема 5. Для любого элемента f, для любой ортонормированной системы {_n} справедливо неравенство (неравенство Парсеваля)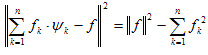

.