Круглий хвилевід

У круглому хвилеводі, як випливає з теорії, поширюються два класи хвиль: поперечно електричні і поперечно магнітні. Хвилі відрізняються одна від одної конфігурацією поля, фазовою швидкістю й критичною частотою. Хвиля з найнижчою критичною частотою називається основною хвилею хвилеводу, інші – вищими типами.

Розглянемо круглий хвилевід радіуса а, показаний на рис. 6.1. Компоненти поля шукаємо в циліндричній системі координат, у якій координати задаються трійкою чисел – r, θ, z.

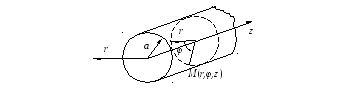
Рис. 6.1. Циліндричний хвилевід кругового перетину

Завдання полягає в знаходженні фазової сталої хвилі β і складових електромагнітного поля в будь-якій точці простору всередині хвилеводу (r < a).

Можна вважати, що у хвилеводі поширюється одна із поперечних електричних хвиль, що біжить уздовж осі z, а сам хвилевід виконаний з ідеального металу, тобто втрати в металевих стінках відсутні.

Для знаходження залежності компонент поля хвиль класу від поперечних координат необхідно знайти корені хвильового рівняння дляразом із граничними умовами на стінці хвилеводу.

; . (6.4)

Розв’язуючи рівняння (6.4) водночас із граничними умовами, знаходимо подовжню складову магнітного поля й поперечне хвильове число:

; (6.5)

m = 0, 1, 2, 3, …, n = 1, 2, 3, … .

де – амплітуда подовжньої складового магнітного поля;

–корені рівняння ;

–функція Бесселя;

–похідна функції Бесселя.

Індекс m показує кількість періодів тригонометричної функції при зміні перемінної на, а індексn – номер кореня рівняння . Фізичний зміст константm і n – кількість варіацій поля вздовж координат φ та r відповідно. У табл. 1 подані кілька перших коренів ν_mn для різних значень m.

Таблиця 6.1. Корені рівняння

n m	1	2	3	4
0 1 2 3	3.821 1.841 3.054 4.201	7.016 5.331 6.706 8.015	10.173 8.536 9.969 11.346	13.324 11.706 13.170

Таблиця 6.2. Корені рівняння

n m	1	2	3	4
0 1 2 3	2.405 3.832 5.136 6.380	5.520 7.016 8.417 9.761	8.654 10.173 11.620 13.015	11.792 13.324 14.796 16.223

Після обчислення подовжньої складової магнітного поля поперечні компоненти можуть бути виражені через за допомогою співвідношень (6.3):

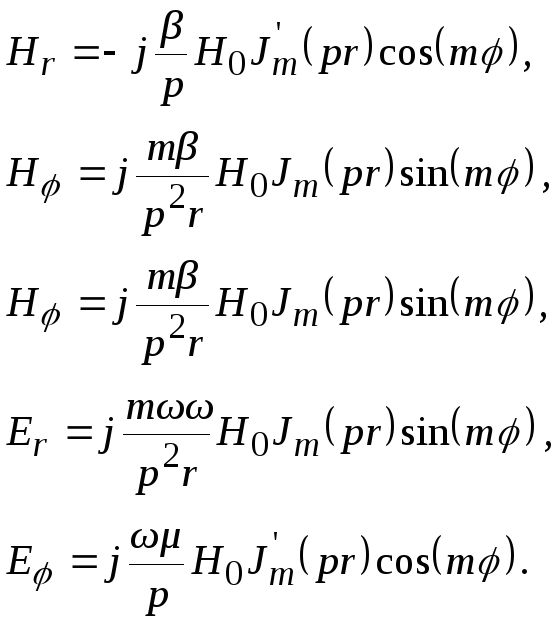(6.6)

Кожній парі констант m, n відповідає конкретна хвиля типу ТЕ, тому що індексів m і n нескінченна безліч, то і хвиль нескінченна кількість. Однак поширюватися вздовж хвилеводу може тільки кінцева кількість хвиль, а саме ті, критичні частоти яких нижче частоти електромагнітної хвилі.

Критична довжина хвилі і довжина хвилі у хвилеводі, при заданих значеннях m і n, можуть бути знайдені з виразів:

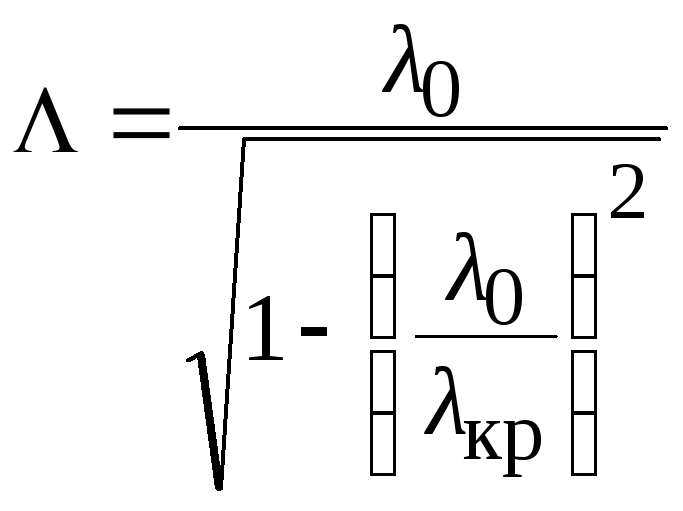, . (6.7)

Для хвиль класу ТМ гранична задача розв’язується аналогічно, але замість рівняння (6.4) записують хвильове рівняння й граничні умови для подовжньої складової електричного поля:

(6.8)

Розв’язуючи це рівняння водночас із граничними умовами, знаходимо подовжню складову електричного поля й поперечне хвильове число:

, ,m = 0, 1, 2, 3, …, n = 1, 2, 3, … , (6.9)

де – амплітуда подовжньої складового електричного поля;

–корені рівняння (табл. 6.2).

Поперечні компоненти можуть бути виражені через , як і в попередньому випадку, за допомогою співвідношень (6.3).

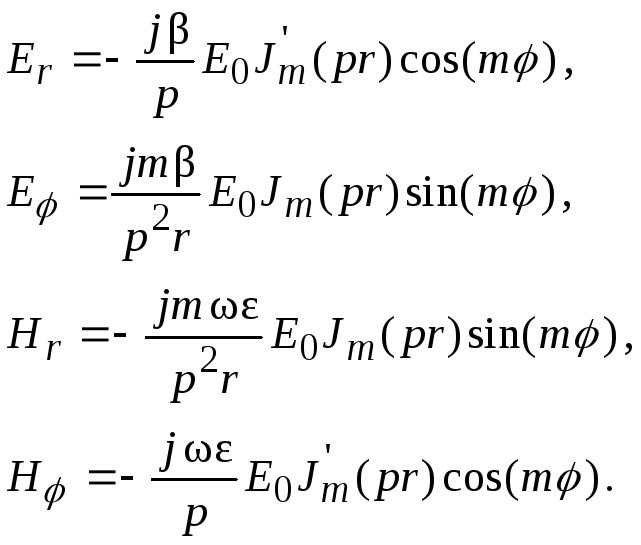(6.10)

Хвиль інескінченна безліч. Вони відрізняються одна від одної конфігурацією поля й критичною частотою. Хвиля з найнижчою критичною частотою називається основною хвилею лінії передачі. З формул (6.5), (6.9) і табл. 6.2 випливає, що найбільшу критичну довжину має хвиля (ТЕ один, один). Отже, вона і є основною хвилею круглого хвилеводу. Критична довжина цієї хвилі

.