3.5 Взаимное расположение прямых.

Две прямых в пространстве могут занимать различное положение друг относительно друга: пересекаться, быть параллельны и скрещиваться.

1. Пересекающиеся прямые (рис. 3.11) имеют общую точку, проекции которой К₁иК₂расположены на одной линии связи.

2. Параллельные прямые пересекаются в несобственной точке. На эпюре одноименные проекции параллельных прямых параллельны, т.е. если ab, тоa₁b₁,a₂b₂,a₃b₃(рис. 3.12).

Для прямых общего положения их параллельность определяется двумя проекциями. Особый случай представляют собой прямые параллельные одной из плоскостей проекций. Например, горизонтальные и фронтальные проекции профильных прямых всегда параллельны. Для оценки взаимного положения следует построить их проекции на ₃. В данном примере прямыеАВиCDпараллельны.

Рис 3.11. Пересекающиеся прямые.

Р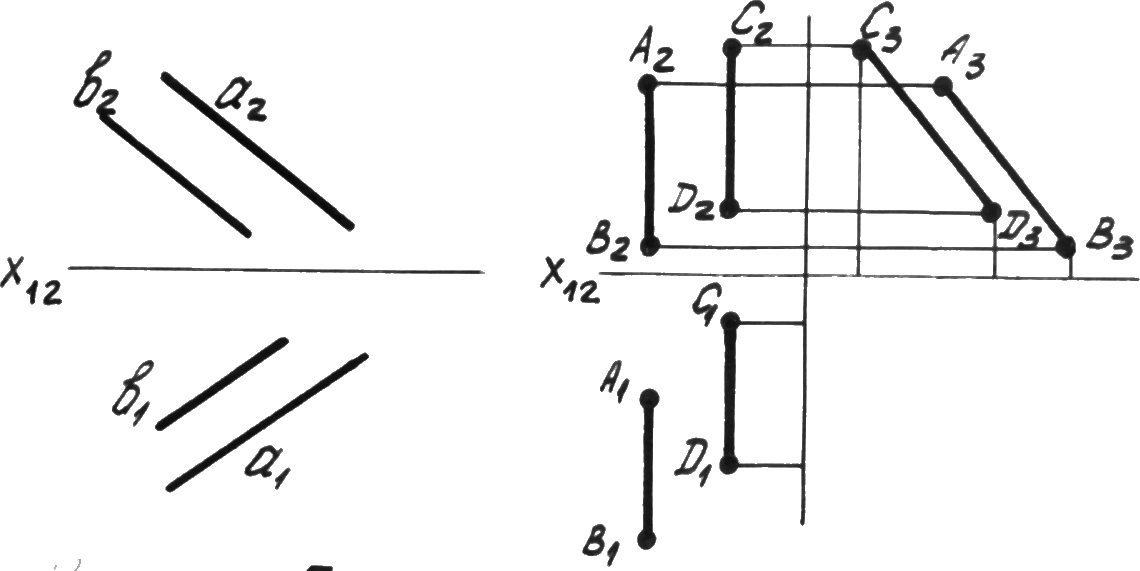ис. 3.12. Параллельные прямые.

Скрещивающиеся прямые не имеют общей точки, а точки пересечения их одноименных проекций не лежат на одной линии связи (рис. 3.13).

Исключение составляет случай, когда одна из скрещивающихся прямых профильная, и для оценки взаимного положения требуется построение проекции на плоскость ₃. В данном примереBEиACскрещиваются. Точки пересечения проекций скрещивающихся прямых лежащие на одной линии связи называютсяконкурирующими. По конкурирующим точкам определяется видимость элементов прямых на соответствующих плоскостях проекций.

Р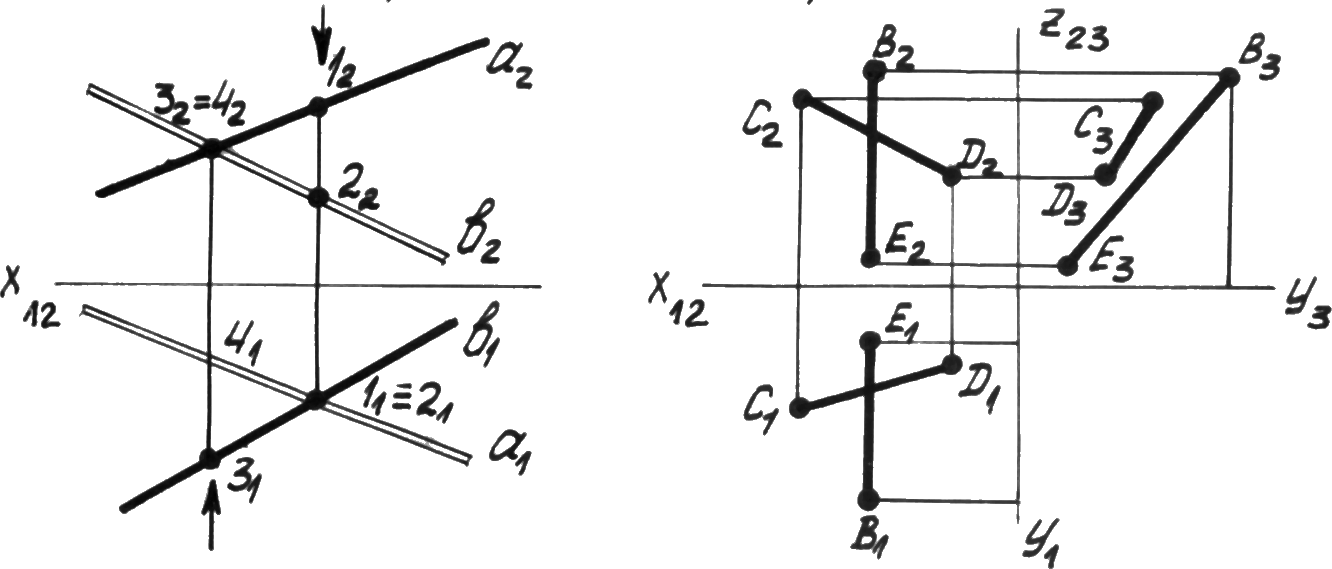ис. 3.13. Скрещивающиеся прямые.

Видимость точек 1 и 2 на горизонтальной плоскости проекций определяется по фронтальной проекции, какая из точек по линии связи расположена выше (указано стрелкой). В данном случае точка 1, принадлежащая прямой авидима на₁.

Видимость точек 3 и 4 на фронтальной плоскости проекций определяется по горизонтальной проекции, какая из точек по линии связи расположена ближе к наблюдателю (указано стрелкой). В данном случае точка 3, принадлежащая прямой bвидима.

Вопросы и задачи для самоконтроля

Когда след прямой будет находиться в бесконечно удаленной, несобственной точке?

Для какой прямой на эпюре следы:

1. лежат на оси проекций;

2. совпадают.

Построить следы прямой, определяемой точками АиВ:

1. А(10, 20, 50);В(20, 50, 10).

2. А(60, 25, 60);В(20, 10, 25).

3. А(10, 15, 50);В(50, 15, 10).

Глава 4. Плоскость

4.1 Способы задания плоскости

Плоскость считается заданной; если из всех точек пространства можно выделить только те точки, которые принадлежат данной плоскости. Плоскость на чертеже может быть определена следующими способами (каждый из способов допускает переход к любому другому способу).

1. Тремя точками, не лежащими на одной прямой (рис. 4.1а).

2. Прямой и точкой вне прямой (рис. 4.1б).

3. Двумя пересекающимися прямыми (рис. 4.1в).

4. Двумя параллельными прямыми (рис. 4.1г).

5. Любой плоской фигурой-отсеком пространства (рис. 4.1д).

Рис. 4.1а. Три точки.

Р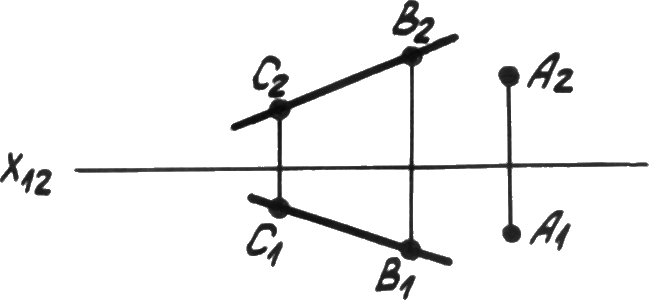ис. 4.1б. Прямая и точка.

Р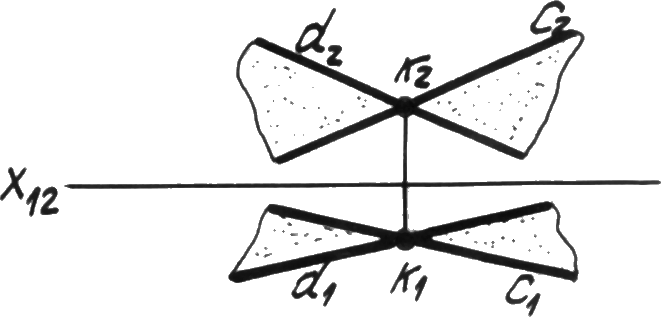ис. 4.1в. Пересекающиеся прямые.

Р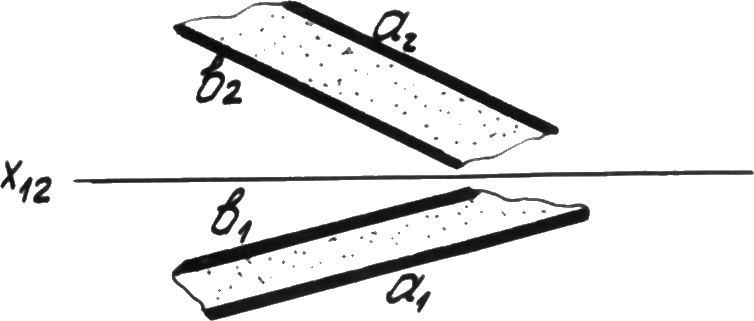ис. 4.1г. Параллельные прямые.

Р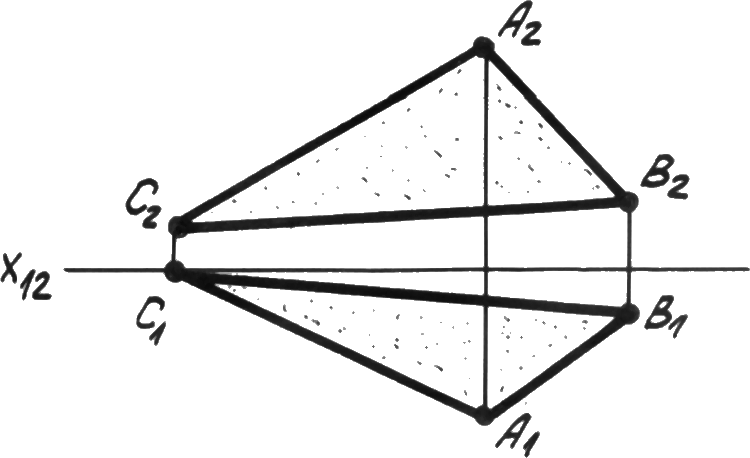ис. 4.1д. Фигура.

6. Следами плоскости (рис. 4.2).

Следы плоскости - это линии пересечения плоскости с плоскостями проекций.

Линия пересечения плоскости с плоскостью ₁называется горизонтальным следом плоскостиQ₁, с плоскостью₂-фронтальным следомQ₂, с плоскостью₃-профильным следомQ₃. Точки пересечения следов на осях проекций называются точками схода следовQ_x,Q_y,Q_z.

Отрезки OQ_x,OQ_y,OQ_z, отсекаемые осями проекций, называютпараметрамиплоскости (рис. 4.2).

Р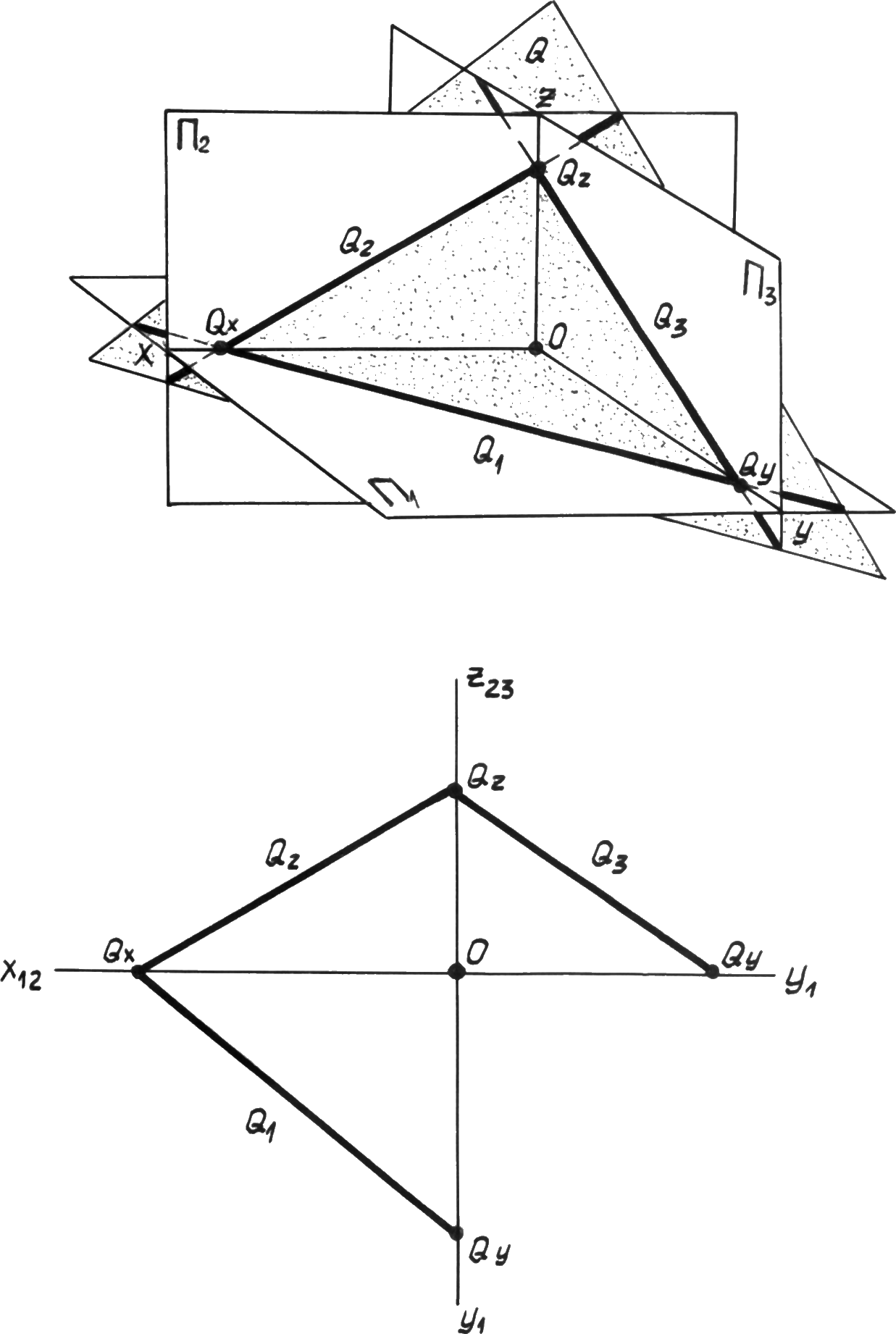ис. 4.2. Следы плоскости.