6.1.3. Развертка многогранника

Разверткой поверхности называется плоская фигура, полученная совмещением поверхности с плоскостью.

Построение разверток важно для тех видов производства, где продукция изготавливается из листового материала. При проектировании листовых конструкций выполняется построение разверток их поверхностей. При построении развертки многогранника необходимо определить натуральную величину всех его граней.

Р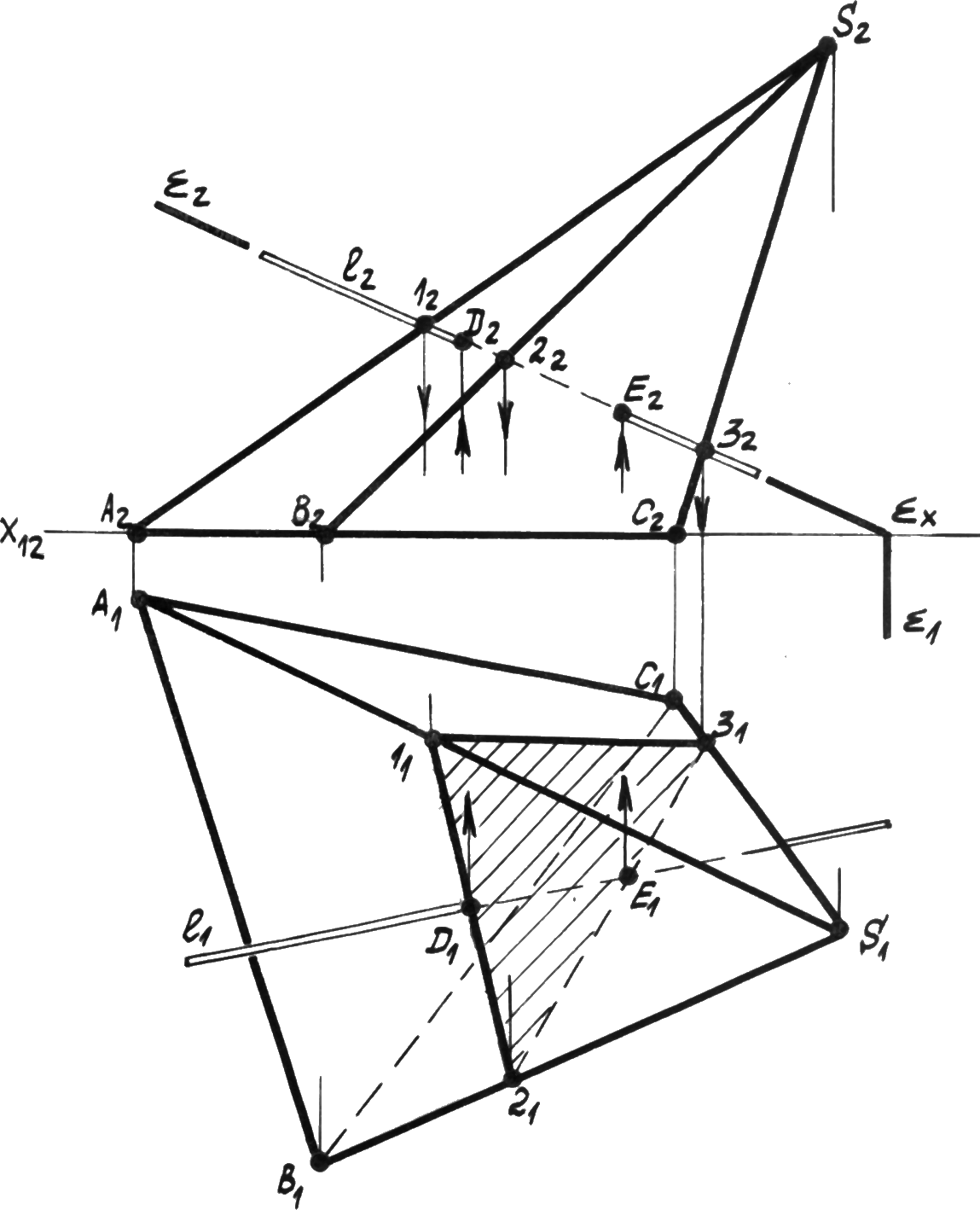ис. 6.4. Пересечение прямой с многогранником.

Существует несколько способов построения разверток: способ нормального сечения, способ раскатки.

Рассмотрим построение развертки призмы способом нормального сечения.

Задача:Дана треугольная призма (рис. 6.5). Построить развертку поверхности данной призмы.

Р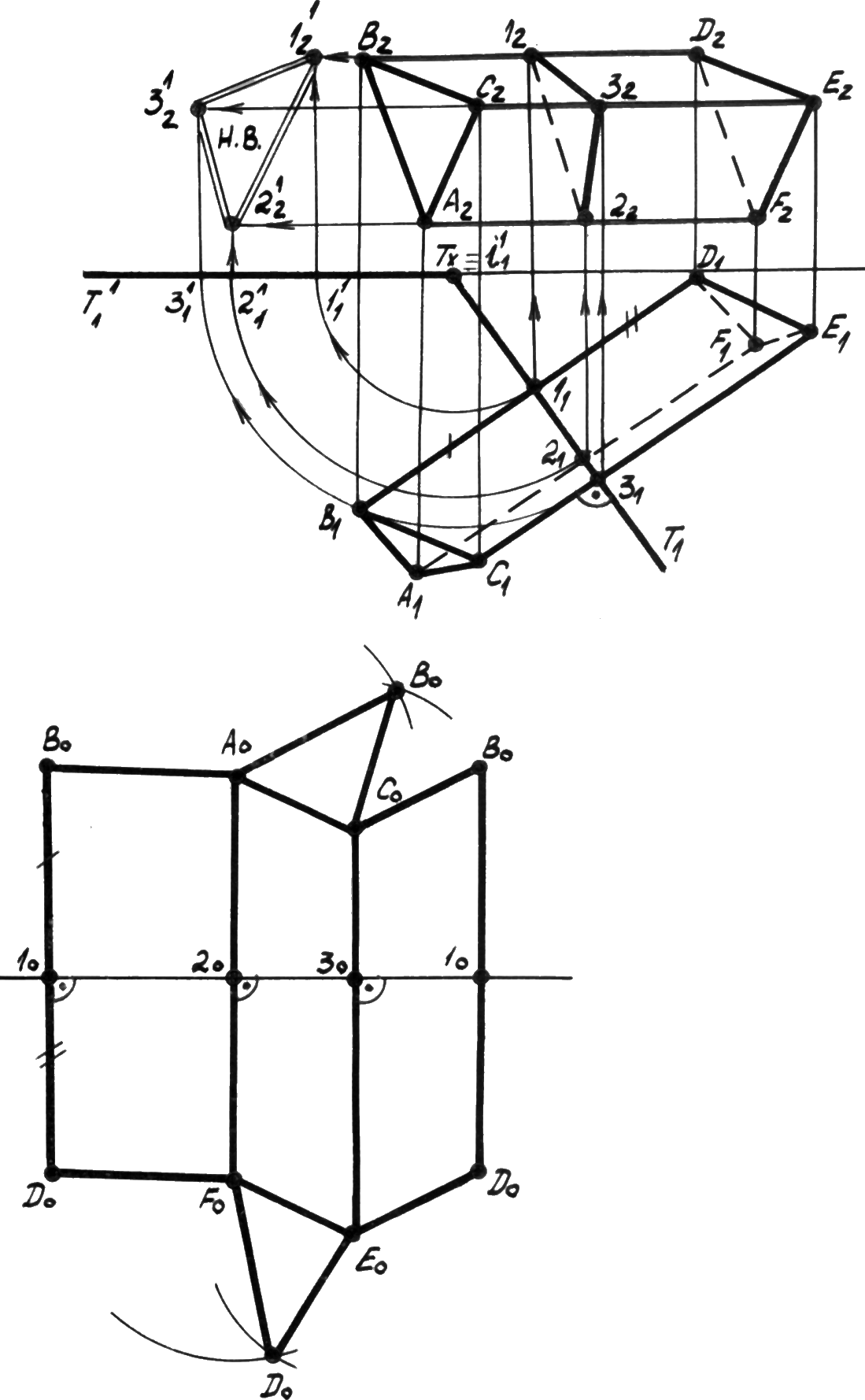ис. 6.5. Развёртка призмы. Способ нормального сечения.

Решение:Пересечем призму плоскостью Т перпендикулярно ее боковым ребрам. Полученное сечение (123) называетсянормальным.Так как ребра призмы в данной задаче являются горизонталями, то след плоскости нормального сечения Т₁перпендикулярен горизонтальным проекциям реберA₁F₁,B₁D₁,C₁E₁. Определяем натуральную величину нормального сечения призмы плоскостью Т способом вращения вокруг осиi. Фигура (123) - натуральная величина нормального сечения.

Для построения развертки на горизонтальной линии отложим отрезки, равные сторонам нормального сечения 1₀2₀12, 2₀3₀23, 3₀1₀  33. Ребра призмы перпендикулярны линии нормального сечения, их натуральную величину измеряем на горизонтальной плоскости(так как ребра являются горизонталями)B₀D₀  B₁D₁,A₀F₀  A₁F₁,C₀E₀  C₁E₁. Полученная фигураB₀A₀C₀B₀D₀E₀F₀D₀являются боковой поверхностью призмы. Для получения полной развертки достраиваем в натуральную величину основания призмы.

6.2. Кривые поверхности

6.2.1. Основные понятия

В начертательной геометрии кривая поверхностьопределяются, как непрерывное множество положений перемещающейся в пространстве линии, называемойобразующей. Образующая может быть прямой линией (линейчатаяповерхность) или кривой (нелинейчатая). Движение образующей в пространстве может осуществляться по некоторому закону. Такая поверхность называетсязакономерной, в отличии отнезакономерной(случайной) поверхности. К числу условий перемещения в пространстве образующей линии относятся: перемещение по неподвижным линиям -направляющим, вращательное движение вокруг неподвижной оси, винтовое перемещение и др.

Одна и та же поверхность может быть образована перемещением различных линий и согласно различных условиям. Например, боковая поверхность прямого кругового цилиндра может быть рассмотрена как результат:

• перемещение окружности вдоль некоторой оси;

• вращение некоторой образующей прямой линии вокруг оси вращения;

• вращение некоторой кривой линии, все точки которой равноудалены от оси вращения.

Рассматривая совокупность прямолинейных образующих с совокупностью образующих окружностей получим каркасданной поверхности цилиндра.

Множество неподвижных линий, инцидентных данной поверхности и объединенных каким либо общим признаком, называется её каркасом.