
- •Основные понятия
- •Задачи, приводящие к дифференциальным уравнениям
- •Уравнение размножения и гибели.
- •Уравнение движения точки на оси
- •Геометрическая интерпретация дифференциального уравнения первого порядка
- •Методы решения некоторых дифференциальных уравнений первого порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные дифференциальные уравнения первого порядка
- •Уравнение в полных дифференциалах
- •Линейные уравнения.
- •Линейные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- •Метод вариации постоянных
Линейные уравнения второго порядка с постоянными коэффициентами
Линейные однородные уравнения второго порядка с постоянными коэффициентами
Решим дифференциальное линейное однородное уравнение второго порядка с постоянными коэффициентами:

(Здесь pиq– числа). Ищем решение
в виде .
Эта функция будет решением (1) тогда и
только тогда, когда
.
Эта функция будет решением (1) тогда и
только тогда, когда – корень уравнения
– корень уравнения
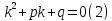
Уравнение (2) называется характеристическим.
Действительно,
подставляя в (1) вместо
 функцию
функцию ,
получаем
,
получаем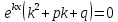 .
Так как экспонента никогда не равна 0,
то на нее можно сократить, и мы приходим
к квадратному уравнению (2).
.
Так как экспонента никогда не равна 0,
то на нее можно сократить, и мы приходим
к квадратному уравнению (2).
Случай 1.
 .
.
Тогда
уравнение (2) имеет два различных
действительных корня
 и
и будет Ф.С.Р. уравнения (1). Тем самым
будет Ф.С.Р. уравнения (1). Тем самым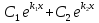 -- общее решение дифференциального
уравнения (1).
-- общее решение дифференциального
уравнения (1).
Случай 2. D=0.
Тогда
характеристическое уравнение (2) имеет
один корень
 и при этом
и при этом . Подставляя в (1) функцию
. Подставляя в (1) функцию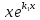 ,
что
,
что
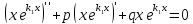
и тем самым
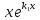 также будет решением, не пропорциональным
решению
также будет решением, не пропорциональным
решению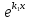 ,
Следовательно, общее решение уравнения
(1) имеет вид
,
Следовательно, общее решение уравнения
(1) имеет вид
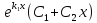
Случай 3.
D<0. Тогда характеристическое
уравнение (2) имеет два комплексно
сопряженных решения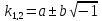 (
(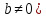 .
Можно проверить, что
.
Можно проверить, что -- два непропорциональных решения
уравнения(1). Отсюда
-- два непропорциональных решения
уравнения(1). Отсюда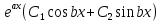 -- общее решение.
-- общее решение.
Пример.Уравнение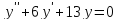 имеет характеристическое уравнение
вида
имеет характеристическое уравнение
вида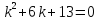 ,
у которого есть пара комплексно
сопряженных корней
,
у которого есть пара комплексно
сопряженных корней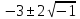 .
Следовательно, общее решение заданного
дифференциального уравнения будет
.
Следовательно, общее решение заданного
дифференциального уравнения будет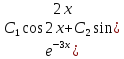
Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
Решаем уравнение

где правая
часть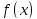 имеет специальный вид, а
имеет специальный вид, а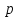 и
и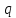 по-прежнему суть числа. Мы применяем
теорему, согласно которой общее решение
уравнения (3) есть сумма общего решения
однородного уравнения (1) и частного
решения (обозначим его
по-прежнему суть числа. Мы применяем
теорему, согласно которой общее решение
уравнения (3) есть сумма общего решения
однородного уравнения (1) и частного
решения (обозначим его )
уравнения (3). Так как общее решение
однородного уравнения мы научились
находить (случаи 1,2,3 выше), то осталось
выяснить в каком виде и как находится
какое-либо частное решение неоднородного
уравнения (3).
)
уравнения (3). Так как общее решение
однородного уравнения мы научились
находить (случаи 1,2,3 выше), то осталось
выяснить в каком виде и как находится
какое-либо частное решение неоднородного
уравнения (3).
Предположим,
что
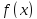 есть функция вида
есть функция вида (здесь
(здесь – многочлен степениn).
– многочлен степениn).
Случай а)
Число
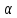 не является корнем характеристического
уравнения (2).
не является корнем характеристического
уравнения (2).
Тогда
частное решение можно найти в виде
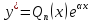 ,
где
,
где -- многочлен степениn.
-- многочлен степениn.
Случай б).
Число
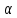 совпадает ровно с одним корнем
характеристического уравнения (2).
совпадает ровно с одним корнем
характеристического уравнения (2).
Тогда
частное решение можно найти в виде ,
где
,
где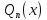 -- многочлен степениn.
Приравнивая коэффициенты при одинаковых
степенях, после подставновки
-- многочлен степениn.
Приравнивая коэффициенты при одинаковых
степенях, после подставновки в уравнение (3), находим коэффициенты
многочлена
в уравнение (3), находим коэффициенты
многочлена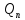 .
.
Случай в).
Число
 -- двукратный корень характеристического
уравнения.
-- двукратный корень характеристического
уравнения.
Тогда
частное решение можно найти в виде
 ,
где
,
где -- многочлен степениn,
-- многочлен степениn,
Подведем
итог и сформулируем вид частного решения,
применимый сразу для всех трех случаев
а), б), в). Для этого определим число
 – кратность показателя
– кратность показателя в характеристическом уравнении – число
корней (2), с которыми совпадает
в характеристическом уравнении – число
корней (2), с которыми совпадает .
По другому, это наибольшее неотрицательное
целое число, такое, что
.
По другому, это наибольшее неотрицательное
целое число, такое, что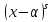 делит
делит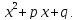 Возможные значения суть 0, 1 или 2.
Существует и третий способ определения
Возможные значения суть 0, 1 или 2.
Существует и третий способ определения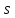 -- это наименьший порядок производной
квадратного трехчлена
-- это наименьший порядок производной
квадратного трехчлена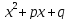 ,
для которой
,
для которой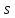 не является корнем.
не является корнем.
Примеры.Для уравнения корни характеристического уравнения
корни характеристического уравнения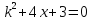 суть числа
суть числа и
и общее решение однородного есть
общее решение однородного есть .
Показатель
.
Показатель равен 0, ибо
равен 0, ибо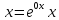 .
Кратность
.
Кратность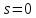 ,
ибо 0 не совпадает ни с -1 ни с -3. Частное
решение ищем в виде
,
ибо 0 не совпадает ни с -1 ни с -3. Частное
решение ищем в виде .
Подставляя это в исходное уравнение,
находим
.
Подставляя это в исходное уравнение,
находим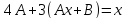 ,
откуда
,
откуда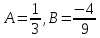 .
Итак
.
Итак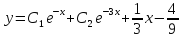 -- общее решение.
-- общее решение.
Уравнение
 имеет корни
имеет корни ,
, ,
откуда видим, что кратность
,
откуда видим, что кратность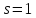 и частное решение надо искать в виде
и частное решение надо искать в виде .
Используя формулу (1), составляем
уравнение для многочлена
.
Используя формулу (1), составляем
уравнение для многочлена :
:
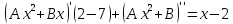
Вычисляя
производные, получим
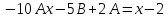 ,
откуда
,
откуда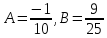 и
и

-- общее решение заданного уравнения.
Пусть теперь
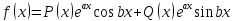 ,
где
,
где )
-- многочлены, наибольшая степень которых
равнаn.
)
-- многочлены, наибольшая степень которых
равнаn.
Случай г)
Комплексное число
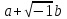 не является корнем характеристического
уравнения (3). Тогда частное решение
можно найти в виде
не является корнем характеристического
уравнения (3). Тогда частное решение
можно найти в виде
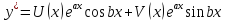
где
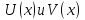 -- многочлены степениnс
неопределенными коэффициентами.
-- многочлены степениnс
неопределенными коэффициентами.
Случай д)
Комплексное число
 (b≠ 0) есть корень
характеристического уравнения. Тогда
частное решение можно найти в виде
(b≠ 0) есть корень
характеристического уравнения. Тогда
частное решение можно найти в виде
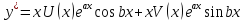
где
 -- многочлены степениnс
неопределенными коэффициентами.
-- многочлены степениnс
неопределенными коэффициентами.
Примеры.Частное решение уравнения ищем в виде
ищем в виде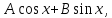 ибо комплексное число
ибо комплексное число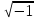 не является корнем уравнения
не является корнем уравнения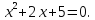 Общее решение имеет вид
Общее решение имеет вид

Частное
решение уравнения
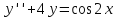 ищем в виде
ищем в виде ибо комплексное число
ибо комплексное число является корнем уравнения
является корнем уравнения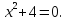 Общее решение уравнения имеет вид
Общее решение уравнения имеет вид

