4. Линейные уравнения.

Задача Коши для уравнения n-го порядка.Рассмотрим дифференциальное уравнениеn-го порядка в нормальной форме

Начальным условием для уравнения (1) называется строка чисел .

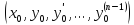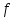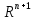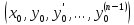Теорема существования и единственности. Пусть функциявместе со своими частными производными по всем переменным, кроме быть может первой, непрерывны в некоторой областиDпространства, содержащей точку. Тогда существует решение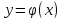уравнения (1) такое, что

Задача Коши для уравнения (1) как раз и состоит в том, что бы найти решение, удовлетворяющее заданным начальным условиям, т.е. для которого верно (2).

Дифференциальное уравнение вида

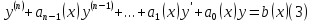
называют линейным неоднородным уравнением или линейным уравнением с правой частью. Если правая часть равна нулю, т.е. если уравнение имеет вид

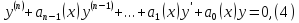
то его называют линейным однородным уравнением. Заметим, что для существования и единственности решения задачи Коши достаточно потребовать непрерывности функций 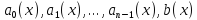. Непрерывность этих функций в дальнейшем предполагается и особо не оговаривается.

В частности дифференциальные линейные уравнения (неоднородное и однородное) второго порядка имеют вид:

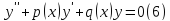
Теорема 1.Сумма двух решений уравнения (6) снова будет решением, и произведение решения на число также будет решением.

Доказательство. Пусть 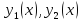-- решения уравнения (6), а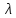-- число. Тогда

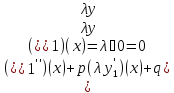
откуда следует, что суть также решения уравнения (6)

Теорема 2.Пусть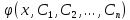-- общее решение однородного уравнения (6), а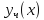-- частное решение неоднородного уравнения (5). Тогдаесть общее решение неоднородного уравнения (5).

Доказательство. Если 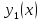есть частное решение однородного уравнения (6), то

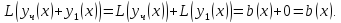
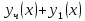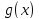Это доказывает, что есть частное решение неоднородного уравнения (5). Наоборот, предположим, чтоесть частное решение неоднородного уравнения (5). Тогда, полагая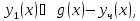получим

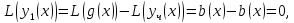
т.е. – решение однородного уравнения (6), причем□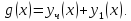

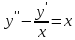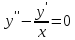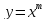Пример.Рассмотрим уравнениеи сопоставим ему однородное уравнение. Будем искать решения этого однородного уравнения в виде степенной функции. Подставляя, получим

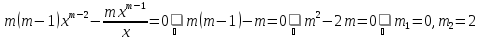
Итак, мы нашли два решения 1 и 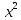уравнения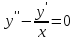. По теореме 1 получаем, что пространство решений этого уравнения включает в себя все функции вида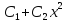. Более того, эта комбинация будет общим решением однородного уравнения. Действительно, какие бы допустимые начальные условиямы ни взяли, всегда можно найти константы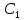и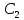такие, что

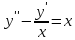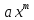Частное решение неоднородного уравнения будем искать также в виде степенной функции. Подставляя, получим

Это дает единственное решение 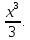Применяя теорему 2, получаем, что

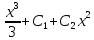
есть общее решение заданного уравнения. Предположим, что нам дополнительно известны начальные условия 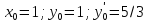. Тогда, составляя систему уравнений

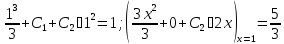
и решая ее, получим 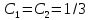, откуда следует, что функцияесть решение задачи Коши уравнения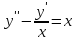cначальными условиями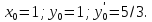

для двух функций, которую можно использовать для понижения порядка однородного дифференциального уравнения, у которого известно одно решение.

Основная теорема о структуре пространства решений однородного линейного дифференциального уравнения.Пусть—не пропорциональные решения. однородного линейного дифференциального уравнения 2-го порядка. Тогда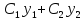есть общее решение этого уравнения.

Доказательство.