
- •Основные понятия
- •Задачи, приводящие к дифференциальным уравнениям
- •Уравнение размножения и гибели.
- •Уравнение движения точки на оси
- •Геометрическая интерпретация дифференциального уравнения первого порядка
- •Методы решения некоторых дифференциальных уравнений первого порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные дифференциальные уравнения первого порядка
- •Уравнение в полных дифференциалах
- •Линейные уравнения.
- •Линейные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- •Метод вариации постоянных
Уравнение движения точки на оси
Пусть
материальная точка массой m движется
вдоль оси Ox, занимая в момент времени
t, положение
 ,
имея мгновенную скорость
,
имея мгновенную скорость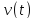 и ускорение
и ускорение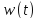 .
Согласно второму закону Ньютона
произведение
.
Согласно второму закону Ньютона
произведение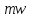 равно сумме действующих сил на точку.
Это представляет из себя дифференциальное
уравнение второго порядка:
равно сумме действующих сил на точку.
Это представляет из себя дифференциальное
уравнение второго порядка:
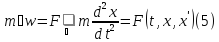
Считаем,
что нам известны положение
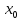 и скорость
и скорость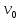 в начальный момент времени
в начальный момент времени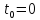 .
Рассмотрим частные случаи.
.
Рассмотрим частные случаи.
А. Свободное
движение. Это случай F=0. Тогда
 -- равномерное движение.
-- равномерное движение.
Б.
Равноускоренное движение. Это случай,
когда F=a -- константа. Тогда
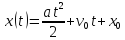 .
.
В. Уравнение
колебаний. Пусть на точку действует
только сила упругости пружины, которая
по закону Гука равна
 ,
где k>0 -- коэффициент жесткости пружины.
Получаем уравнение свободных колебаний
,
где k>0 -- коэффициент жесткости пружины.
Получаем уравнение свободных колебаний
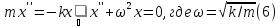
Можно
проверить, что
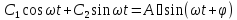 есть целое семейство решений этого
уравнения. Более того, если задано
положение точки
есть целое семейство решений этого
уравнения. Более того, если задано
положение точки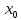 и
скорость
и
скорость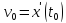 в начальный момент времени
в начальный момент времени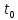 ,
то положение ее в любой момент времени
строго определено. Это значит, что
найдутся единственные константы
,
то положение ее в любой момент времени
строго определено. Это значит, что
найдутся единственные константы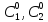 такие, что
такие, что
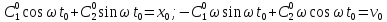
Если на
материальную точку кроме упругой силы
действует и сила сопротивления вязкой
среды,
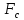 ,
причем она пропорциональна скорости и
направлена в противоположную к скорости
сторону:
,
причем она пропорциональна скорости и
направлена в противоположную к скорости
сторону: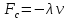 (λ>0 – коэффициент
вязкости), то получаем уравнение
колебаний с учетом сопротивления:
(λ>0 – коэффициент
вязкости), то получаем уравнение
колебаний с учетом сопротивления:
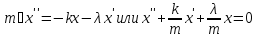
Если на
материальную точку кроме силы упругости
и силы сопротивления действует еще и
вынуждающая сила
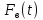 ,
зависящая от времени, то получаем
уравнение вынужденных колебаний :
,
зависящая от времени, то получаем
уравнение вынужденных колебаний :
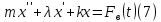
Уравнение колебаний мы решим в параграфе 15.
Геометрическая интерпретация дифференциального уравнения первого порядка
Дано дифференциальное уравнение первого порядка
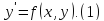
Пусть D- область определения функции .
В каждой точке (x,y)∈Dнарисуем отрезок с
коэффициентом наклона равным
.
В каждой точке (x,y)∈Dнарисуем отрезок с
коэффициентом наклона равным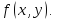 Получим поле направлений на областиD. Кривая γ будет интегральной
кривой, т.е. графиком решения уравнения
(1) тогда и только тогда, когда в любой
точкеP∈γ она касается соответствующего
направления. Тем самым поле направлений
помогает качественно оценить вид
решений, не решая дифференциального
уравнения.
Получим поле направлений на областиD. Кривая γ будет интегральной
кривой, т.е. графиком решения уравнения
(1) тогда и только тогда, когда в любой
точкеP∈γ она касается соответствующего
направления. Тем самым поле направлений
помогает качественно оценить вид
решений, не решая дифференциального
уравнения.
Пример.Рассмотрим уравнение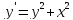 (не решаемое в квадратурах). Нарисуем
поле направлений.
(не решаемое в квадратурах). Нарисуем
поле направлений.
интегральная кривая 

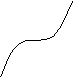

Геометрическую интерпретацию можно применить для приближенного решения дифф. уравнения.
Методы решения некоторых дифференциальных уравнений первого порядка
Определение.Общим решением дифференциального
уравнения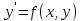 (*) в области
(*) в области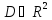 называется такая функцияy=𝜑(x,C), что
называется такая функцияy=𝜑(x,C), что
1) для любого
значения константы C,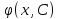 -- решение дифференциального уравнения
(*);
-- решение дифференциального уравнения
(*);
2) для любых
начальных условий
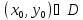 найдется константа
найдется константа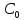 такая, что
такая, что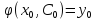 .
.
Например,
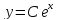 -- общее решение дифференциального
уравненияy'=yна всей декартовой плоскости, а
-- общее решение дифференциального
уравненияy'=yна всей декартовой плоскости, а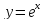 -- частное решение, или решение задачи
Коши с начальным условием
-- частное решение, или решение задачи
Коши с начальным условием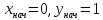 .
.
Уравнения с разделяющимися переменными
Дифференциальное уравнение вида
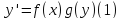
называется уравнением с разделяющимися переменными. Метод решения этого уравнения следующий:
а) разделяем
переменные и получаем уравнение в
дифференциалах :
 ;
;
б) интегрируем
уравнение в дифференциалах
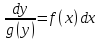 (константуCзаписываем лишь одну)
-- получаем общее решение в неявном виде;
(константуCзаписываем лишь одну)
-- получаем общее решение в неявном виде;
в) выражаем yчерезxиC-- получаем общее решение в явном виде.
Заметим, что такой же метод решения применим и дифференциальному уравнению в дифференциалах, имеющему вид
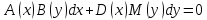
Пример.
Решим дифференциальное уравнение,
описывающее протекание химической
взрывной реакции --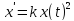 .
Здесьx(t)
-- количество вещества, -- продуктов
взрыва в момент времениt,
аk>0 -- коэффициент
пропорциональности. Методом, изложенном
выше, разделяем переменные
.
Здесьx(t)
-- количество вещества, -- продуктов
взрыва в момент времениt,
аk>0 -- коэффициент
пропорциональности. Методом, изложенном
выше, разделяем переменные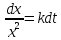 ,
интегрируем --
,
интегрируем --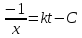 и находим общее решение
и находим общее решение Если
Если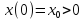 ,
то
,
то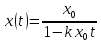 и количество вещества становиться
бесконечным за конечное время
и количество вещества становиться
бесконечным за конечное время .
.
