
- •Основные понятия
- •Задачи, приводящие к дифференциальным уравнениям
- •Уравнение размножения и гибели.
- •Уравнение движения точки на оси
- •Геометрическая интерпретация дифференциального уравнения первого порядка
- •Методы решения некоторых дифференциальных уравнений первого порядка
- •Уравнения с разделяющимися переменными
- •Однородные уравнения
- •Линейные дифференциальные уравнения первого порядка
- •Уравнение в полных дифференциалах
- •Линейные уравнения.
- •Линейные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения второго порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- •Метод вариации постоянных
Однородные уравнения
Так называются уравнения вида
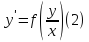
Метод
решения: а) переходим к новой неизвестной
функции
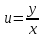 .
Тогда
.
Тогда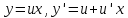 и уравнение (2) переписывается так:
и уравнение (2) переписывается так: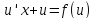 (*). А это уравнение с разделяющимися
переменными.
(*). А это уравнение с разделяющимися
переменными.
б) Решаем
вспомогательное уравнение (*). Пусть
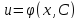 есть его общее решение.
есть его общее решение.
в) Тогда
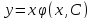 -- общее решение исходного уравнения.
-- общее решение исходного уравнения.
Пример (форма прожектора).Найдем форму прожектора. Нам нужно решить дифференциальное уравнение
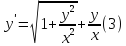
Заменяя
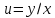 ,
получим
,
получим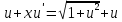 ,
откуда
,
откуда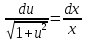 .
Интегрируя, получаем
.
Интегрируя, получаем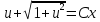 .
Переносяuв право, и
возводя в квадрат, имеем:
.
Переносяuв право, и
возводя в квадрат, имеем:
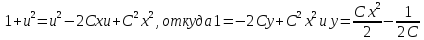
-- семейство парабол с фокусом в начале координат.
Линейные дифференциальные уравнения первого порядка
Так называются уравнения вида
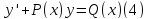
Если P(x),Q(x) непрерывны, то условия теоремы существования и единственности выполнены.
Метод решения
а) Решаем
сначала уравнение
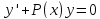 без правой части как уравнение с
разделяющимися переменными. Получаем
общее решение в видеy(x)=Cu(x), где
без правой части как уравнение с
разделяющимися переменными. Получаем
общее решение в видеy(x)=Cu(x), где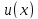 -- одна из первообразных функции
-- одна из первообразных функции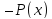 .
.
б) Общее решение уравнения (4) ищем в виде y=C(x)u(x), гдеC(x) -- функция, подлежащая определению. Такой приём называется методом вариации постоянных.
в) Подставляя
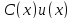 в (4), имеем:
в (4), имеем:
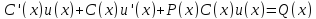
Второе и
третье слагаемые в левой части дают 0,
ибо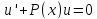 .
Отсюда
.
Отсюда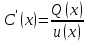
г) Решая это уравнение, т.е. интегрируя, находим
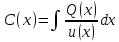
д) Подставляя
это в
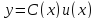 ,
получаем общее решение исходного
уравнения.
,
получаем общее решение исходного
уравнения.
Пример.Сила тока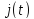 в электрической цепи с омическим
сопротивлениемRи
коэффициентом самоиндукцииLудовлетворяет дифф. уравнению
в электрической цепи с омическим
сопротивлениемRи
коэффициентом самоиндукцииLудовлетворяет дифф. уравнению
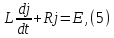
где E-- электродвижущая сила. Найдём зависимостьj(t) при
условии, что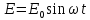 .
Полагая сначалаE=0 находим
.
Полагая сначалаE=0 находим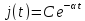 ,
где
,
где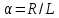 .
Тогда решение исходного уравнения ищем
в виде
.
Тогда решение исходного уравнения ищем
в виде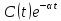 .
ФункциюC(t)
находим из уравнения
.
ФункциюC(t)
находим из уравнения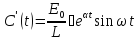 .
Интеграл функции
.
Интеграл функции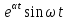 равен
равен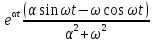 (см. глава «Определенный интеграл»,
последний параграф). Отсюда
(см. глава «Определенный интеграл»,
последний параграф). Отсюда
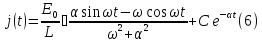
В частности, в установившемся режиме (время tвелико) амплитуда колебаний будет равна
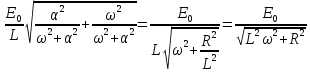
При
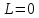 надо вместо уравнения (5) решать уравнение
надо вместо уравнения (5) решать уравнение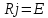 (
закон Ома). Получаем
(
закон Ома). Получаем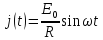
Уравнение в полных дифференциалах
Дифференциальное уравнение вида
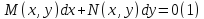
называется
уравнением в дифференциалах. Заметим,
что (1) действительно дифференциальное
уравнение первого порядка, ибо оно может
быть переписано для области D,
в которойN(x,y)≠
0 как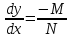 .
Наоборот, любое дифференциальное
уравнение первого порядка может быть
записано в дифференциалах.
.
Наоборот, любое дифференциальное
уравнение первого порядка может быть
записано в дифференциалах.
Уравнение
(1) назовём уравнением в полных
дифференциалах, если в рассматриваемой
области существует функция
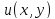 ,
называемая потенциалом, дифференциал
которой равен левой части уравнения,
т.е.
,
называемая потенциалом, дифференциал
которой равен левой части уравнения,
т.е.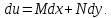
Уравнение
в полных дифференциалах может быть
переписано в виде du(x,y)=0
общим решением которого являются
эквипотенциальные кривые, задаваемые
соотношениемu(x,y)=C.
Докажем это. Пусть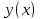 -- неявно заданная уравнением
-- неявно заданная уравнением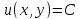 функция. Тогда
функция. Тогда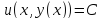 .
Вычисляя дифференциал левой и правой
части, получим:
.
Вычисляя дифференциал левой и правой
части, получим: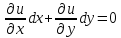 ,
следовательно
,
следовательно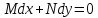 .
.
С другой
стороны, пусть
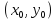 -- начальные условия. Тогда возьмем
константу
-- начальные условия. Тогда возьмем
константу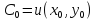 и определим функцию
и определим функцию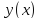 как неявно заданную уравнением
как неявно заданную уравнением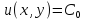 .
Получим решение задачи Коши с заданными
начальными условиями. Доказано, что
.
Получим решение задачи Коши с заданными
начальными условиями. Доказано, что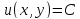 – общее решение.
– общее решение.
Теорема.
Пусть
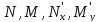 непрерывны в некоторой односвязной
областиD. Тогда
(1) будет уравнением в полных дифференциалах
в том и только том случае, когда в этой
области выполнено условие
непрерывны в некоторой односвязной
областиD. Тогда
(1) будет уравнением в полных дифференциалах
в том и только том случае, когда в этой
области выполнено условие
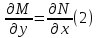
Доказательство части "и только том случае" следует из теоремы о смешанных производных:
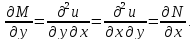
Пусть верно
(2). Ищем функцию
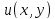 из
условия
из
условия
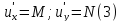 .
.
Выберем
начальную точку
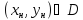 .
Из первого уравнения системы (3), интегрируя
на отрезке
.
Из первого уравнения системы (3), интегрируя
на отрезке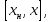 находим:
находим: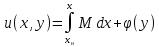 .
Тогда
.
Тогда
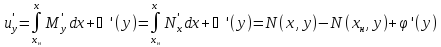
Следовательно,
второе уравнение системы (3) получает
вид
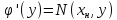 ,
откуда находим
,
откуда находим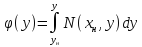 .
Окончательно получаем формулу вычисления
потенциала
.
Окончательно получаем формулу вычисления
потенциала
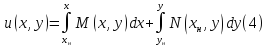
Пример. Найдем общий интеграл уравнения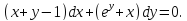 Во-первых
проверим, что это уравнение в полных
дифференциалах
Во-первых
проверим, что это уравнение в полных
дифференциалах
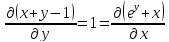
Возьмём
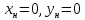 .
Тогда
.
Тогда
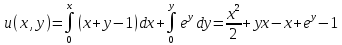
Откуда
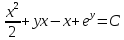 -- общее решение в неявном виде.
-- общее решение в неявном виде.
