Тригонометрические функции

Длина окружности пропорциональна радиусу окружности. Обозначим половину длины единичной окружности через . Тогда

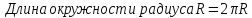
Число -- важнейшая мировая константа. Ее приближенное значение

Рассмотрим единичную окружность . Точкуусловно назовем началом этой окружности. Пусть задано неотрицательное число. Отложим от началадугу окружностидлиныв направлении вращении против часовой стрелки (положительное направление вращения). Если, то наша дуга займет всю окружность и еще останется отложить дугу длинойв положительном направлении. Если и(т.е) то процедуру придется повторить. Но за конечное число шагов мы придем в точку, лежащую на окружности. Ясно, что. Для отрицательного числа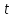следует откладывать дугу длинойв отрицательном направлении вращения, т.е. против часовой стрелки. 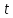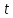Итак, для любого действительного числамы получаем точкуна окружности, такую, что длина дугиотличается отна целое кратное. Точкаимеет координаты. Эти координаты есть функции от. Первая из них, абсцисса, называется косинусом числа, а вторая – синусом:

Теорема Пифагора дает основное тригонометрическое тождество:

Функции тангенс и котангенс определяются уже число алгебраически

Существует множество тригонометрических тождеств. Особенно нам потребуются следующие:

Замечательные пределы Первый замечательный предел

Составим теперь табличку значений функции при. Так как, то мы снова сталкиваемся с раскрытием неопределенности “0/0” .

Мы видим, что значения функции приближаются к единице по мере того, как аргумент стремится к нулю. Однако никакое алгебраическое преобразование нам не поможет раскрыть эту неопределенность. Прибегая к оценкам площадей фигур и свойствам предела, мы докажем, что

На рис. -- длина дуги. Из рисунка видно, что приимеют место неравенства

Но

Отсюда получаем неравенства 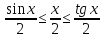. Поделим все части этого неравенства на>0, получим. Обратим дроби и выводим. Отметим также, что заодно мы доказали неравенствопри. Так как функцииичетные, то для любых ненулевыхс модулем меньше π /2 имеют место неравенства

Тогда

-- стремится к 0, откуда . Левая часть двойного неравенства в (2) также имеет предел равный 1. По теореме о пределе промежуточной функции получаем требуемое равенство.

Второй замечательный предел

Теорема.Существует предел функцииприи оно равен e. Это же число е равно пределу функциипри.

Непрерывность функции

Определение.Функция, определенная в окрестности точки, называется непрерывной в этой точке, если. Функция непрерывна на отрезке (интервале), если она непрерывна в каждой точке этого отрезка (интервала).

Это определение можно переписать так: функция непрерывна в точке , если

,

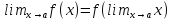т.е. когда две операции над переменной -- функцияfи предельный переход перестановочны.

Обозначим -- приращение переменной и-- приращение функции. Тогда определение непрерывности можно переписать и так:непрерывна в точкеa, если.

Свойства непрерывных функций

Н1.Сумма непрерывных функций суть непрерывная функция

Н2.Произведение непрерывных функций суть непрерывная функция

Н3.Частное непрерывных функций суть непрерывная функция, во всех точках, где знаменатель отличен от 0

Эти свойства являются непосредственным следствием соответствующих свойств пределов (см. LIM2-LIM4, ).

Н4.Подстановка непрерывной функции в непрерывную функцию есть непрерывная функция

Это свойство следует из свойства LIM8 -- предел сложной функции.

Устойчивость знака непрерывной функции.Пустьнепрерывна в точкеaи. Тогдадля всехxдостаточно близких к.

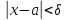Доказательство. Для найдетсятакое, что как только, то. Для этих значенийимеем:□

Примеры непрерывных функций

1. Константа, а также тождественная функция непрерывны.

Доказательство вытекает из LIM1.

2. Любой многочлен непрерывная функция.

Применяем Н1 и Н2 к тождественной функции

3. Рациональная функция, т.е. отношение двух многочленов, непрерывная функция в точках не являющихся корнями знаменателя.

Применяем Н3 к многочленам.

4. Функция непрерывна.

Действительно, (применяем неравенствополученное при выводе первого замечательного предела). Отсюда следует, что, т.е.непрерывна в точке.