Системы электродинамических потенциалов и уравнения математической физики для гармонического электромагнитного поля

Для вектора магнитной индукции всегда выполняется условие , поэтому

,

где – комплексный векторный магнитный потенциал.

, поэтому

где – комплексный скалярный электрический потенциал,

и – система электродинамических потенциалов.

Во многих случаях корректное задание поля вектора в качестве объёмно распределенного источника ЭМП вызывает значительные затруднения при постановке задачи анализа поля. В этих случаях вместо задают векторное поле

, которое называют полем сторонней плотности магнитного тока. С учётом этого обозначения закон электромагнитной индукции можно записать в виде:

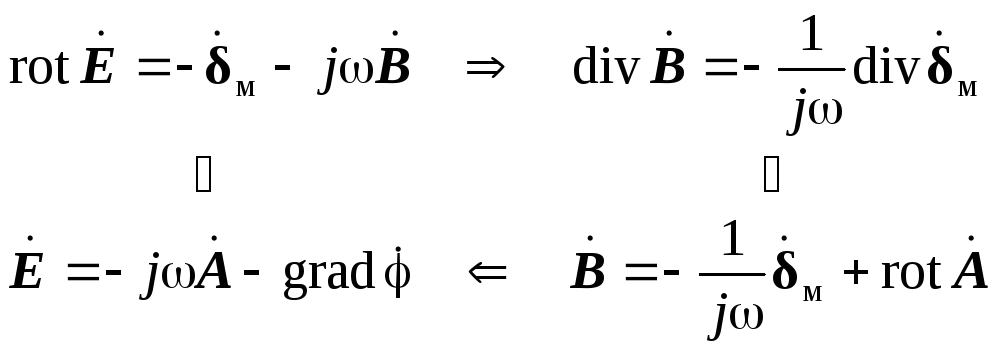
Теперь можно получить систему уравнений математической физики относительно потенциалов. За основу можно взять закон полного тока

; ;

;

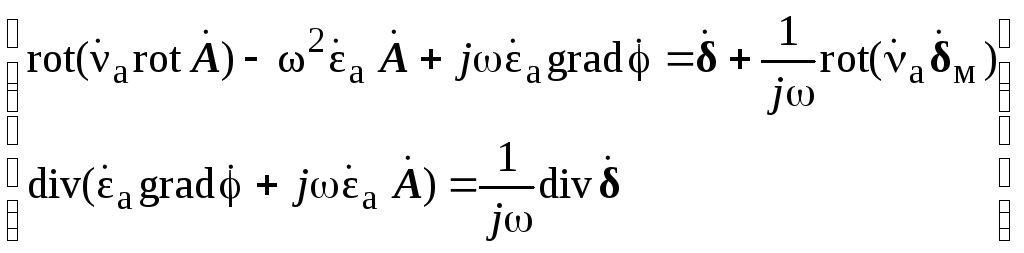(1)

(1) – комплексная форма системы уравнений математической физики относительно векторного магнитного и скалярного электрического потенциалов. Нетрудно заметить, что уравнения в системе (1) линейно зависимые (второе можно получить из первого взятием дивергенции от обеих частей и делением их на jω). Поэтому для обеспечения единственности решения системы уравнений (1), кроме граничных условий, нужно вводить условие калибровки электродинамических потенциалов.

Рассмотрим систему (1) для случая однородной по электрофизическим свойствам среды внутри расчетной области. Тогда скалярные поля параметров и можно вынести за знак дифференциальных операторов и умножить обе части первого уравнения на .

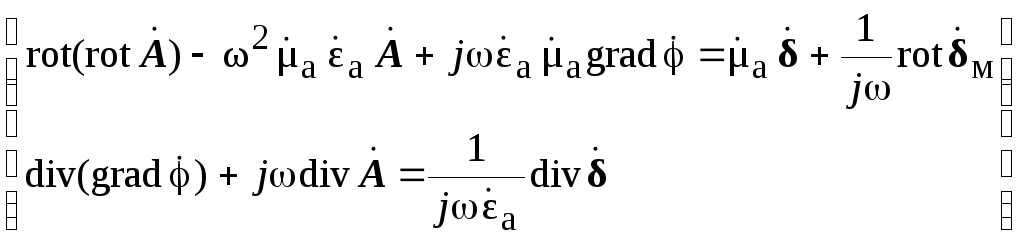(2)

Если к системе (2) применить условие калибровки Лоренца

,

то из (2) можно получить два независимых уравнения:

, (3)

, (4)

где – фазовая скорость электромагнитной волны.

Уравнение (3) называется векторным уравнением Даламбера, уравнение (4) – скалярным уравнением Даламбера. Если источники ЭМП отсутствуют в расчетной области, то правая часть этих уравнений равна нулю:

, (5)

, (6)

где – пространственная частота ЭМП.

Уравнения (5) и (6) называют векторным и скалярным волновыми уравнениями. Они широко применяются на практике для расчета разнообразных электротехнических и радиотехнических устройств, входящих в состав различного радиоэлектронного оборудования и приборов.

Излучатель Герца

Условно можно считать, что этот излучатель представляет собой малый отрезок провода, по которому течет гармонически изменяющийся ток. При расчетах такой излучатель можно считать материальной точкой с гармонически изменяющимся электрическим дипольным моментом. Аналитические выражения для распределения электродинамических потенциалов вокруг этого излучателя являются фундаментальными решениями уравнений (5) и (6)

,

.

Элементарный магнитный излучатель

Условно можно считать, что этот излучатель представляет собой контур с гармонически изменяющимся током. При расчетах такой излучатель можно считать материальной точкой с гармонически изменяющимся магнитным дипольным моментом . Аналитическое выражение для распределения векторного магнитного потенциала вокруг этого излучателя является фундаментальным решением уравнения (5):