4. Определение внешних моментов и построение эпюр крутящих моментов

Крутящие моменты в поперечных сечениях бруса возникают, если приложена внешняя сила, не проходящая через ось, или внешний момент Т_е. Величина момента от силы F определяется как произведение силы на плечо (см. рис. 5), например, в зубчатой передаче:

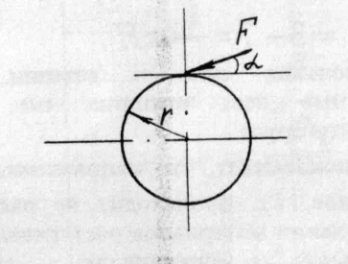
Рис. 5

Зачастую требуется определить внешний момент по передаваемой мощности Р (Вт) и частоте вращения вала n (об/мин)

,

где – угловая скорость, рад/с.

Она определяется по формуле:

.

В круге 2 радиан, за 1мин. будет совершенно 2n радиан, а за секунду – в 60 раз меньше, поэтому получится приведенная формула.

Брус, работающий на кручение, называют валом.

Крутящие моменты Т, т.е. моменты, возникающие между частицами материала и действующие в плоскости сечения, определяют методом сечений.

Пусть один конец бруса жестко заделан, а к свободному концу Приложены три внешние момента (см. рис. 6).

Рис. 6

Моменты принято изображать, как показано на рисунке. Крестик означает, что сила приложена от нас, точка – к нам. Такое изображение дает четкое представление в каком направлении действует момент.

Выполним сечение 3-3 и рассмотрим статическое равновесие правой части бруса. В сечении 3-3 будет возникать крутящий момент Т₃. Его направление мы не знаем, поэтому примем произвольно, например, как у Т_е3. Если при нахождении значения оно окажется отрицательным, то направление следует сменить на противоположное. Составим уравнение статического равновесия. За положительное примем направление, как у Т_е1. Это правило знаков должно сохраняться до конца решения задачи.

;

.

Вывод: крутящий момент в сечении равен алгебраической сумме внешних моментов, приложенных к рассматриваемой части бруса.

Согласно вывода, в сечении 2-2:

,

а в сечении 1-1:

.

Определив значения крутящих моментов, строят эпюру.

Пример. Для вала определить, значения крутящих моментов и построить, их эпюру. Данные приведены на рисунке 7.

Рис  7

Решение: Будем рассматривать левую часть вала. В сечении 1-1 крутящий момент равен:

.

Поскольку для крутящих моментов нет установленного правила знаков, то примем его положительным.

В сечении 2-2:

.

В сечении 3-3:

.

Строим эпюру Т. Знаки крутящих моментов на эпюре можно не проставлять, так как мы сами дали им обозначения положительных и отрицательных.

Проверка правильности построения эпюры: в сечениях, где приложен внешний момент, эпюра делает скачок на величину этого момента.