105. . 106. . 107. .

108. 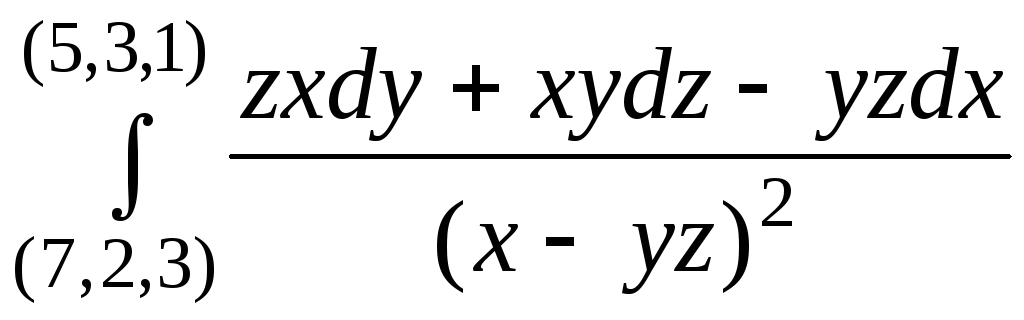(контурное интегрирование не пересекает поверхность .

Найти первообразную функцию и по полному дифференциалу:

109. .

110. .

111. .

112. .

113. . 114.

С помощью формулы Грина вычислить КИ-2:

115. , гдеl – окружность .

116. , гдеl – эллипс .

117. Вычислить , гдеl – простой замкнутый контур, пробегаемый в положительном направлении. Указание. Рассмотреть случаи: 1) начало координат находится вне контура l; 2) контур l окружает начало координат.

118. В каждой точке эллипса приложена сила, равная по величине расстоянию от точкиM до центра эллипса и направленная к центру эллипса. Найти работу при перемещении в положительном направлении: а) вдоль дуги эллипса в первом октанте; б) вдоль всего эллипса.

119. Сила по величине обратно пропорциональна расстоянию точки ее приложения от оси Oz , перпендикулярна к этой оси и направлена к ней. Найти работу этой силы по окружности от точкидо точки.Указание. .

14.6. Поверхностные интегралы

14.6.1. Двусторонние поверхности и их ориентация

Гладкая поверхность  называется двусторонней поверхностью , если при возвращении в исходную точку после обхода замкнутого контура , лежащего на  и не имеющего общих точек с ее границей, направление нормали к поверхности не меняется.

Совокупность всех точек поверхности с приписанными в них по указанному правилу нормалями называется определенной стороной поверхности.

Выбор определенной стороны поверхности называется ориентацией поверхности. Выбранная сторона - это положительная сторона поверхности. Для замкнутой поверхности положительной считается внешняя сторона.

Если  задана неявным уравнением , то сторона характеризуется одним из единичных нормальных векторов

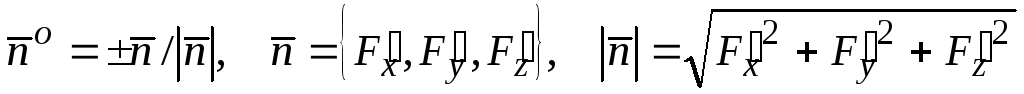. (6.1)

Если  задана явным уравнением ,, то сторона характеризуется одним из векторов:

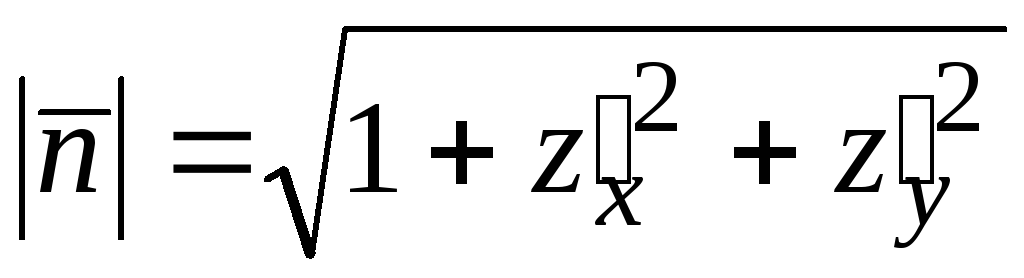, . (6.2)

14.6.2. Поверхностный интеграл первого рода (пи-1)

Пусть : 1) в точках двусторонней гладкой (или кусочно-гладкой) поверхности  из пространства , ограниченной кусочно-гладким контуром, определена ограниченная скалярная функция; 2) - произвольное разбиение  на n частей с площадямии диаметрами; 3) - произвольный набор точек;

4)- интегральная сумма, соответствующая данному разбиению поверхности  и выбору точек .

Определение. Конечный предел интегральной суммы при,не зависящий ни от способа разбиения поверхности, ни от выбора точек , называетсяповерхностным интегралом первого рода от функции по поверхности:

.

Вычисление ПИ-1. Теорема 14.10. Если : 1) поверхность  задана неявным уравнением иесть решение этого уравнения приили- решение уравнения при, или-решение уравнения при, где- проекции на плоскости - соответственно, 2) между точками и ее соответствующей проекцией установлено взаимно однозначное соответствие, то

, (6.3)

причем ПИ-1 существует, если существуют соответствующие двойные интегралы.

Здесь координаты вектораи находятся по формулам (6.1). ПИ-1 не зависит от выбора стороны поверхности.

Следствие. При явном задании  : в силу (6.2) из (6.3) получим

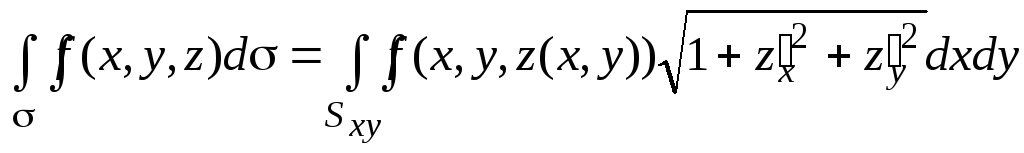. (6.4)

Некоторые приложения ПИ-1

1. Масса материальной поверхности. Пусть 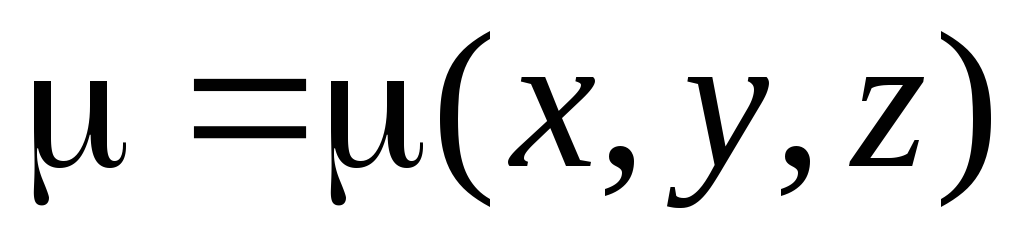- поверхностная плотность материальной поверхности площади s. Тогда масса этой поверхности .

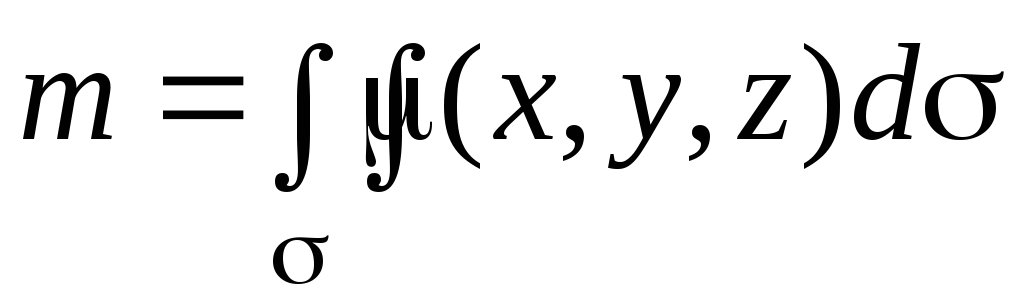2. Площадь искривленной поверхности  . Если принять в предыдущей формуле 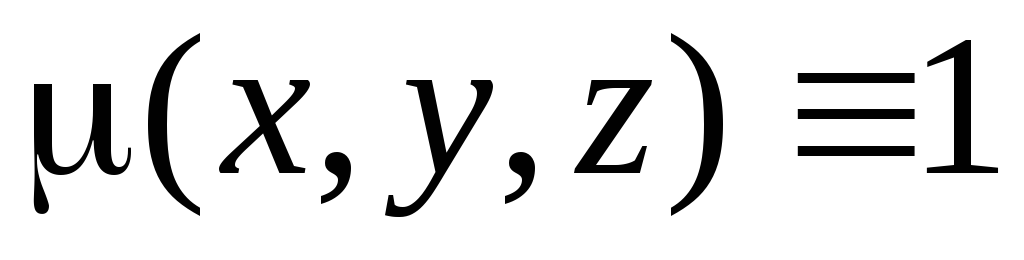, то масса поверхности числено равна площади s , т.е. .

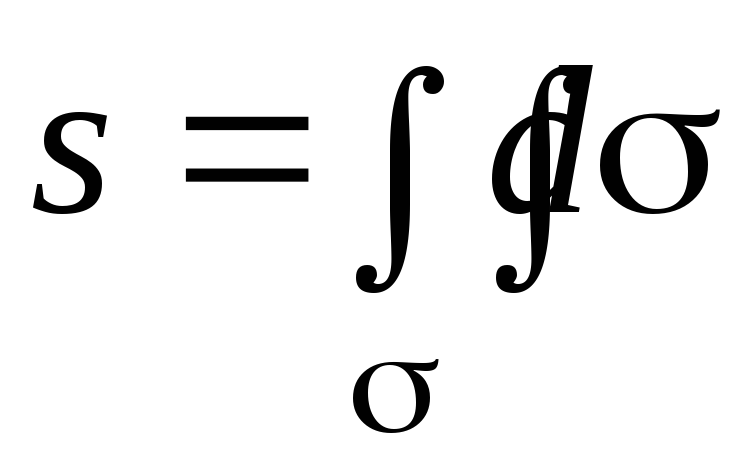3. Статические моменты материальной поверхности  с поверхностной плотностью 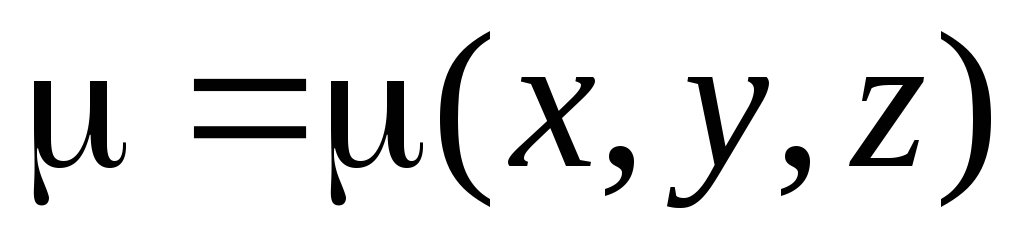и массой m относительно плоскостей 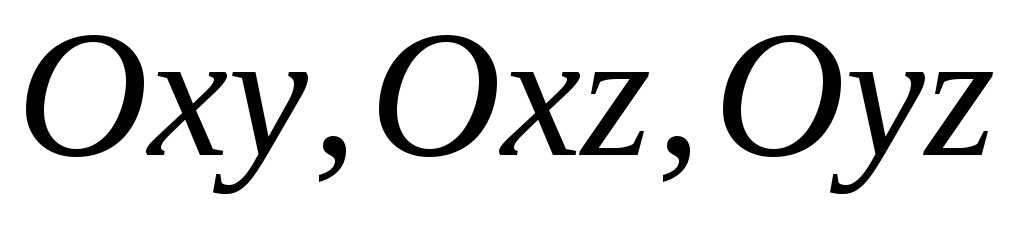соответственно равны: ,,.

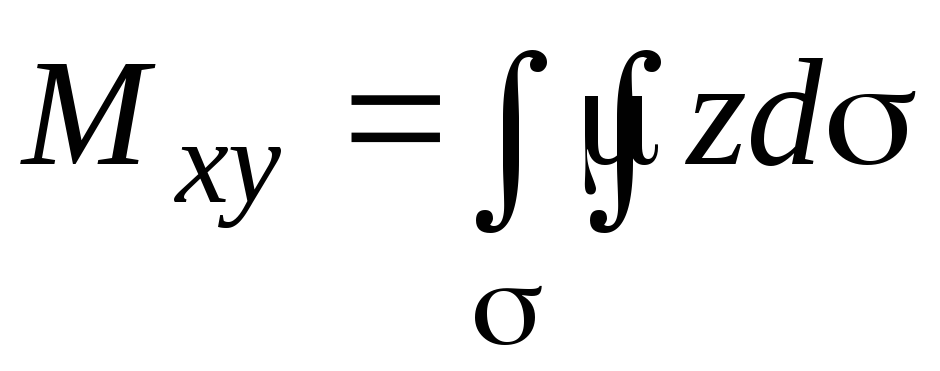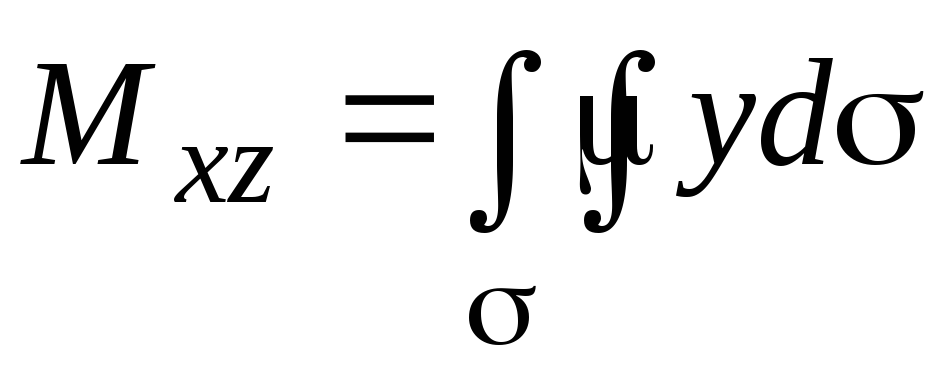4. Координаты центра тяжести материальной поверхности  :

.