15.1.3. Линейный интеграл вектора. Циркуляция векторного поля

Пусть поле - непрерывное векторное поле, (L) – кусочно гладкая кривая с выбранным на ней положительным направлением (ориентированная кривая).

Определение 1.Линейным интегралом (обозначается) векторавдоль ориентированной кривой (L) называется криволинейный интеграл

(1.7)

Для линейного интеграла справедливы следующие формулы:

(1.8)

=.

Если поле есть силовое поле, то линейный интеграл (1.7) дает величину работы этого поля вдоль линии (L). Вычисление линейного интеграла в зависимости от задачи может быть проведено по одной из формул “списка” (1.8).

Определение 2.Циркуляцией (обозначаетсяЦ) векторного поляназывается линейный интеграл по замкнутой ориентированной кривой (L):

. (1.9)

За положительное направление обхода замкнутой кривой (L) берется то, при котором область, ограниченная кривой, лежит под левой рукой.

Пример 1.Найти линейный интеграл векторавдоль дуги (L) винтовой линииот точкиAпересечения линии с плоскостьюz=0 до точкиВпересечения с плоскостьюz=1.

Решение. Имеем по последней формуле из списка (1.8): . ТочкеAсоответствует значение параметраt=0, точкеB– значениеи, таким образом,.

Пример 2.Вычислить работу силового полявдоль отрезкапрямой, проходящей через точкии.

Решение.Работа.

Запишем канонические уравнения прямой . Отсюда; параметры. Вычислим работу:.

Пример 3.Вычислить циркуляцию полявдоль эллипса.

Решение. Имеем по формуле (1.9) и (1.8): . Запишем параметрические уравнения эллипса:. Вычисляяdxиdy, получим:- здесь использовано, что(вычисление этих интегралов проводится с помощью понижения степени подынтегральной функции).

Пример 4.Вычислить циркуляцию векторного полявдоль линииL, полученной пересечением конусас координатными плоскостями (см. рис.4).

Р

Рис. 4.

ешение. ЛинияLсостоит из двух отрезковBCиCA, расположенных на координатных плоскостяхOyzиOxzсоответственно, и дугиокружности. Для циркуляции имеем:.1) На отрезкеBCимеем:. Следовательно,. 2) На отрезкеCAимеем:. Следовательно,. 3) На дугеABокружностиимеем:и=. Искомая циркуляция поля равна нулю.

Пример 5.Вычислить циркуляцию векторного полявдоль линии,.

Решение. Имеем: . ЛинияLесть эллипс, получающийся в результате сечения цилиндраплоскостью. Найдем параметрические уравнения этой линии. Проекция любой точки этой линии на плоскостьOxyнаходится на окружности. Отсюда, полагая, найдем, что. Дляzиз уравненияполучим:. Таким образом,. Находим отсюда:, и для циркуляции запишем определенный интеграл:.

15.1.4. Дивергенция векторного поля

Интегральные характеристики – поток и линейный интеграл – характеризуют векторное поле “в целом”. Количественную характеристику поля в каждой точке дают, вводимые ниже, дифференциальные характеристики. Введем понятие дивергенции.

Окружим произвольную точку Mповерхностью (S) произвольной формы (например, сферой достаточно малого радиуса). Пусть (V) – объем, заключенный внутри поверхности (S).

Определение.Конечный предел отношения потока поля через поверхность (S) к объему, заключенному внутри нее при стягивании поверхности к точкеMи стремлении объемаVк нулю называется дивергенцией векторного поляв точкеM:

(1.10)

Замечание.Определение (1.10) есть инвариантное (не зависящее от системы координат) определение дивергенции.

Дивергенция характеризует отнесенную к единице объема мощность потока векторного поля, “исходящего” из точки M, то есть мощность источника (при), или стока (при), находящегося в точкеM.

В декартовой системе координат дивергенция вычисляется по формуле

. (1.10)

Свойства дивергенции. Пусть и- векторные поля,- скалярная функция. Тогда:

1) ; 2) . (1.11)

С учетом формулы (1.10) перепишем формулу Гаусса-Остроградского (1.6)

(1.12)

- поток векторного поля через замкнутую поверхность (S) равен тройному интегралу по объему (V), заключенному внутри этой поверхности от дивергенции поля.

Пример 1.Вычислить.

Решение. .

Пример 2.Вычислить, гдеu(M) – скалярная функция,- векторная функция.

Решение. По формуле (1.10) находим: .

Пример 3.Используя теорему Гаусса-Остроградского (1.12), найти поток векторного полячерез всю поверхность (S) тела (V):

в направлении внешней нормали.

Решение. Имеем . Поэтому=. Для вычисления тройного интеграла перейдем к цилиндрическим координатам. Уравнение поверхности примет вид,=.
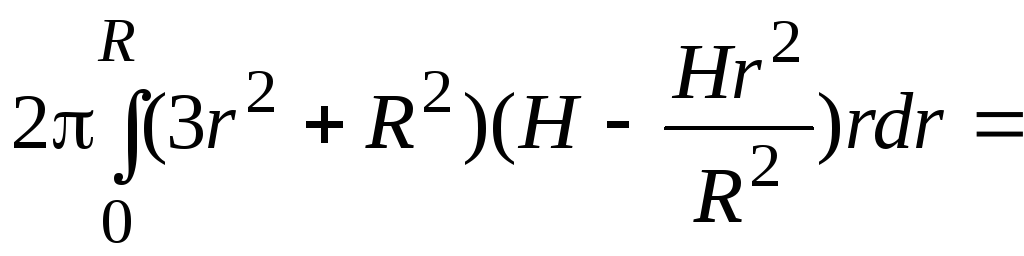